定义
所谓整数平方根即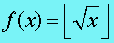 。
。
算法
算法1.猜试法
利用等差级数公式:
![]()
这样的话, ![]() 从1开始一直算到数列的前项和第一次大于x的时候,
从1开始一直算到数列的前项和第一次大于x的时候,![]() 即是所求。下面给出source code(C):
即是所求。下面给出source code(C):
这种方法无异于穷举法,其唯一的优点是:每次的迭代用到了前面迭代的结果,所以会有一些效率的增益。对于该算法的改进就是不穷举,改用我们熟悉的二分查找法来做。
算法2 Newton 法
把这个问题转换为方程求根问题,即:![]() ,求x。
,求x。
而方程求根的问题可以用Newton 法来解决。现在的问题有一点不同,即所求的根必须是整数。通过证明,我们可以发现,Newton迭代公式是适用于整数情况的,于是有:
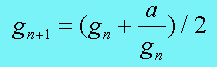
至于是怎么证明的,可以参考hacker’s delight。
另外,初值的选择也是很重要的一环,这里我们选择大于等于![]() 的最小的2的幂次数。
的最小的2的幂次数。
OK,下面给出程序:
算法3 逐比特确认法
逐比特确认法认为一个32位整数求根,结果应该是一个16位整数。求这个16位整数,其实质是确认每位的比特是0还是1.我们把这个根分为两个相加的部分,一部分是已确认的值,另一部分是未确认的值。从高位到低位,每次迭代确认一位。初始时,已确认部分为0。则问题的初始形式为:
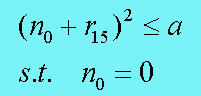
算法发明者为:James Ulery 论文:Computing Integer Square Roots
下面给出源代码:
性能比较
在0~1000000范围内对四种算法进行了遍历性的测试,得到测试结果:
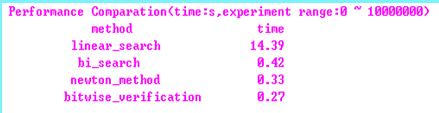
显见四种算法的遍历性能以逐比特确认法为最好,逐比特确认法从本质上来说是一种二分查找法,而且其查找范围为整个16位整数域;而我们实现的二分查找法的查找范围到已知变量为止,从范围上来说比逐比特确认法来得小,但是最后平均性能却不及逐比特确认法。其原因在于:逐比特确认法把问题分解为相同的子问题的集合,采用递推的方法,很好地利用了前面步骤的结果,不用什么都从头算起,从而避免了重复劳动,用加减法和移位操作代替了乘除法操作,最终获得了性能上的增益。
需要注意的是,虽然平均性能有如此的关系。并不代表每个数或每组数都有这样的关系。实际上,我们每组产生1000个随机数,并对每组的算法性能进行了测试,各个算法都有获得优胜的时候。至于具体是什么场合用什么算法,需要分析和经验的支撑。目前,我所能归纳出的概要指导准则为:
(1)在大多数情况下,牛顿迭代都能获得不错的性能,
(2)逐比特确认法更适合运算数比较大的场合。
测试环境说明:操作系统: windows xp sp3
CPU : Pentium4 3.0GHZ
内 存: 2.40GHz 0.99GB
编译环境: VC++6.0企业版
参考文献
1. hacker’s delight 之 初等函数
2. 完全平方数的判定及整数平方根的快速求解 http://hi.baidu.com/atyuwen/blog/item/206369fdae6d221e09244da9.html
3. James Ulery Computing Integer Square Roots
期间曾因为算法细节问题,向James Ulery求教并得到其热情回复,向其表示感谢。
4. 计算正整数平方根的整数部分(J2ME)
http://www.360doc.com/content/060601/10/233_126245.html
本文结束。