((08 ext{年江苏卷}))满足条件(AB=2,AC=sqrt{2}BC)的三角形(ABC)的面积的最大值是(underline{qquadqquad}).
解析:
建立如图所示坐标系,设$$A(-1,0),B(1,0).$$设(C(x,y),)则由(AC=sqrt{2} BC)
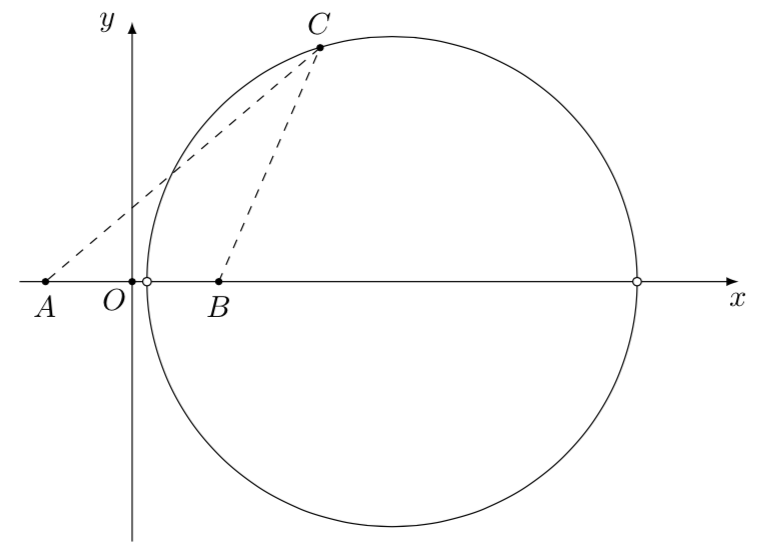
可得$C$点的轨迹方程$$sqrt{left(x+1 ight)^2+y^2}=sqrt{2}cdot sqrt{left(x-1 ight)^2+y^2},y eq 0.$$ 整理可得$$(x-3)^2+y^2=8,y eq 0.$$从而$ riangle ABC$的面积最大值为$$ dfrac{1}{2}cdot |AB|cdot 2sqrt{2}=2sqrt{2}.$$