一些记号
• 图: 由两个集合{V,E}所组成,记作G(V,E)
• V是图中顶点(Vertex)的非空有限集合。
• E是图中边(Edge)的有限集合。
• 子图(subgraph):边的子集,以及相关联的点集
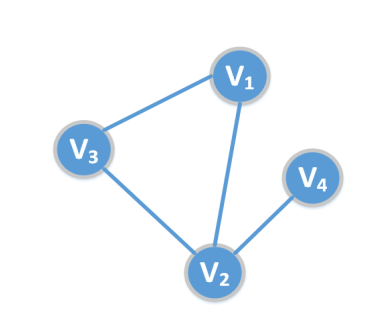
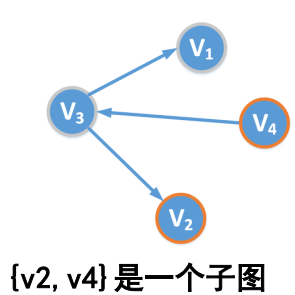

• 邻接(adjacent):在无向图中,如果边(u,v)∈E,则u和v互为邻接点。
在有向图中,如果弧<u,v>∈E,则v是u的邻接点。
• 路径(path):图中一个顶点序列称路径,路上相邻顶点都是邻接的。
如v到v’的路径为(v=V0, V1, V2, …, Vn=v’),并且
<V0,V1><V1,V2>…<Vn-1,Vn>∈集合E。
• 如果顶点和边都不重复出现,则称为简单路径。
• 除了起点和终点相同外没有重复顶点的路径,称为环(cycle)。

SPT
• 从结点s出发的单源最短路构成一棵树(最短路树, SPT)
松弛
• 对于一条有向边<u,v>
d[v] = min(d[v], d[u]+w[u][v])
• 称为边(u,v)上的松弛操作(relaxation)。
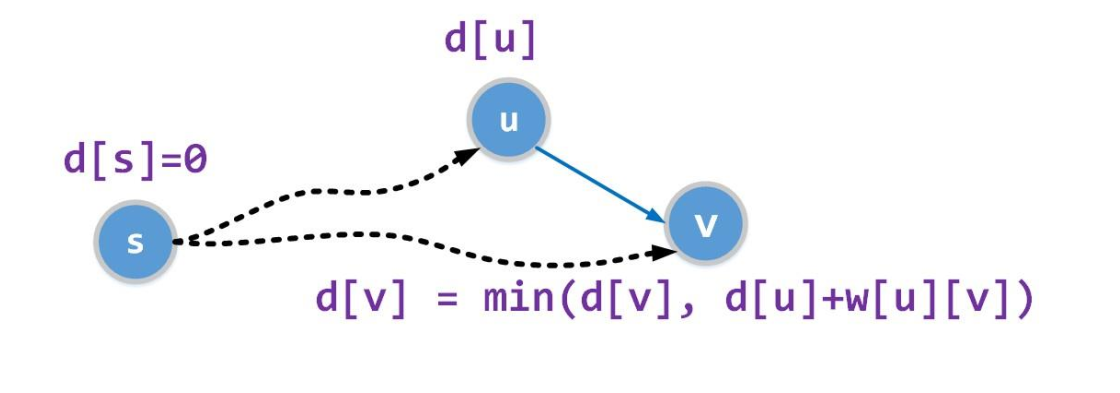

松弛一条边(u,v), 即测试是否可以通过起点u,
对目前找到的v的最短路d[v]进行改进。
若可以改进,更新d[v]。 松弛只会减小d[v]。
松弛是改变最短路径的唯一方式;
Dijkstra的过程就是通过不断松弛使d[i]从∞收敛至dis[i]。
关于松弛

• 三角不等式:对任意边<u,v>∈E, 有 dis[v] ≤ dis[u]+w(u,v)
• 上界性质:算法过程中, 对任意顶点 v∈V, 有 d[v] ≥ dis(s,v),
而且一旦d[v]达到dis(s,v)值就不再改变(松弛只会减小d[v]) 。
• 无路径性质:若从s到v不存在路径, 则总是有d[v] = dis(s,v) = ∞
• 收敛性质:如果图G中边e<u,v>在s到v的最短路径上, 考察路径s到u到v,
若算法中在松弛边<u,v>之前的任何时间有d[u] = dis(s,u), 则在操
作过后总有d[v] = dis(s,v)。
• 路径松弛性质:如果 p = <v0,v1, …, vk> 是从S=v0到vk的最短路径,
而且p中的边按照<v0,v1><v1,v2>…<vk-1,vk>的顺序进行松弛, 那么最
后d[vk] = dis(s,vk)。 这个性质的保持并不受其他松弛操作的影响,
即使他们与p中边上的松弛操作混合在一起
最短路径的最优子结构性质
• 若p = <v1,v2,…,vk>是v1到vk的最短路径, 对于其中的
任意一段1≤i≤j≤k, pij = <vi,…,vj>必是v i到v j的最短
路径。 (反证法)
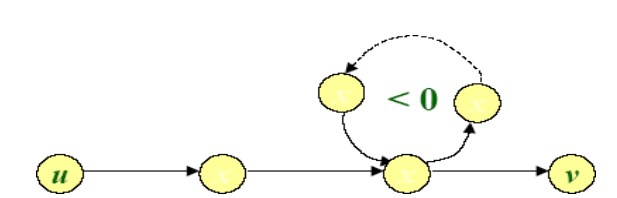
• 如果存在一条从s可达的负权回路, 则s到该回路上的顶点
之间就不存在最短路径。
• 最短路不能包含负权回路, 同时也不会包含正权回路。
Dijkstra——所有边权值非负
Bellman-Ford——允许存在负
权边, 但不能有负权回路
Bellman-Ford算法
• 解决含负权边的带权有向图的单源最短路径问题
• G无负权回路,则输出最短路
• G有负权回路,则输出无解
• 最短路最多只经过(起点不算)N-1个结点,根据路径松弛性质,可
以通过N-1轮松弛操作得到。

上述算法称为Bellman-Ford算法, 它的时间复杂度为O(VE)。
第k轮松弛的结果
• 第k轮松弛之后, 数组d [ i ]的意义是什么?
• d [ i ]为从s出发最多经过k条边到达结点i 的最短路径长度;
当然此处假设无负权回路。
• 算法的最终目的是在V-1轮松弛之后, 计算出从s出发最
多经过V-1条边到达结点i 的最短路径长度。
• 如果在某轮松弛之中所有结点的d [ i ] 都没有改变, 那么
Bellman-Ford算法就可以提前结束了(类似冒泡排序)
判负环
• 在进行完V-1轮松弛之后, 再对每条边加一轮松弛, 如果
此时有的边仍旧可以被松弛, 意味着G包含s可达的负权
回 路, 最短路不存在。
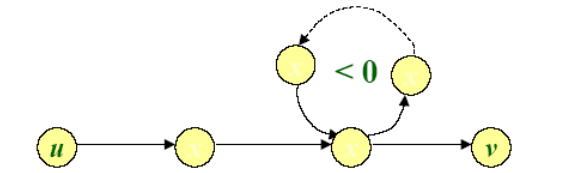
• 证明:
▫ 如果成立, 则说明找到了一条经过了n条边的从u到v的路径,
且其比任何少于n条边的从u到v的路径都短。
▫ 一共n个顶点, 路径却经过了n条边, 则必有一个中间顶点k
经过了至少两次。 则k是一个回路的起点和终点。 走这个回
路比不走这个回路路径更短, 只能说明这个回路是负权回路。
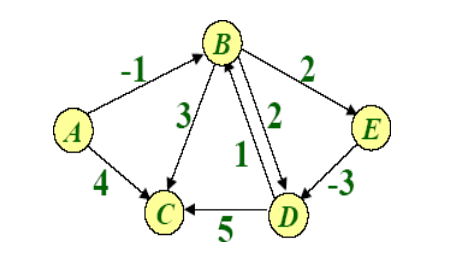
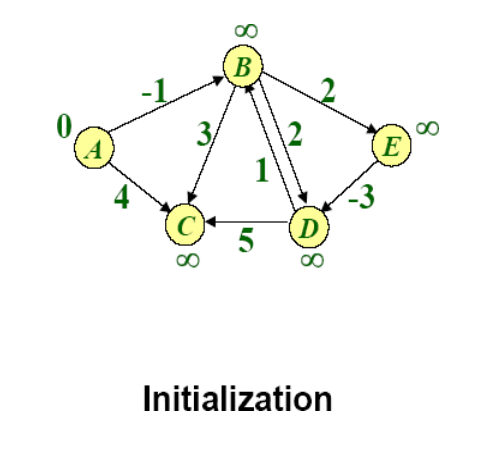
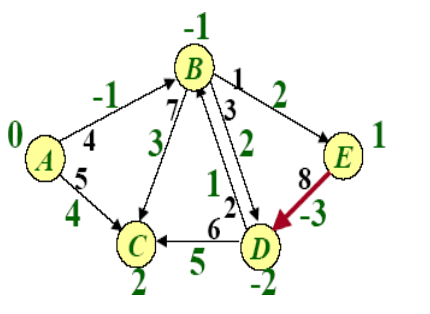
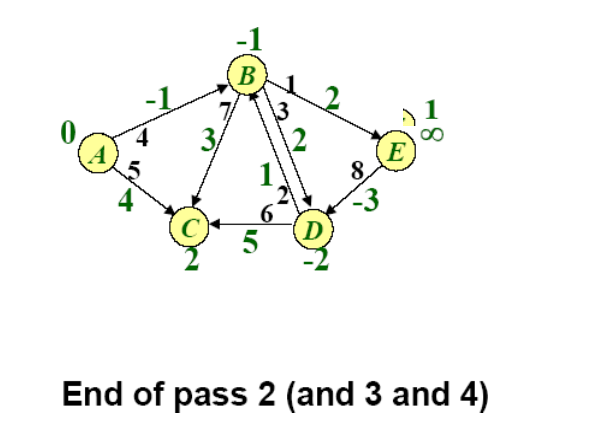
Example of BellmanFord
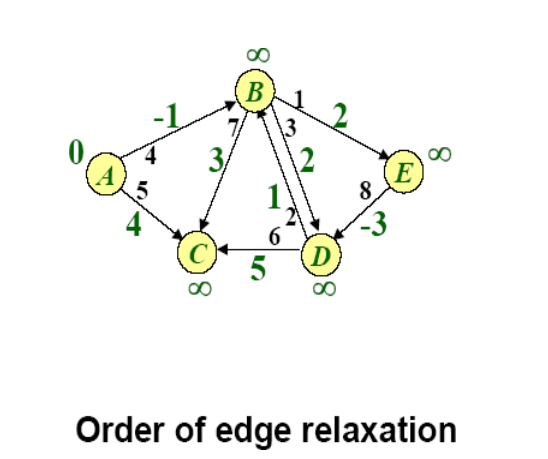
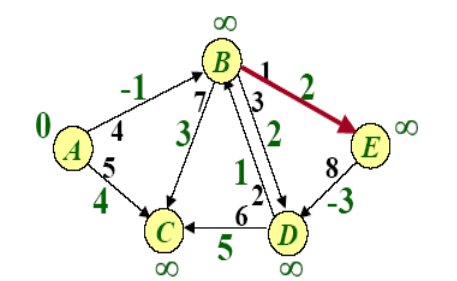
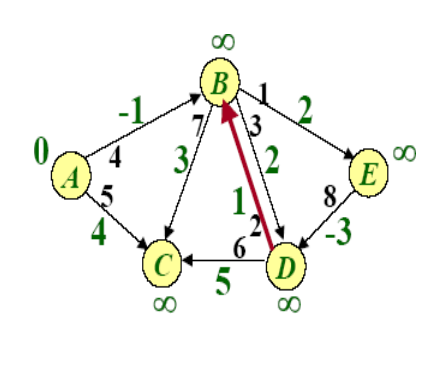
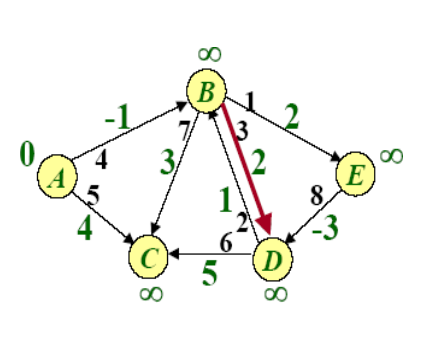
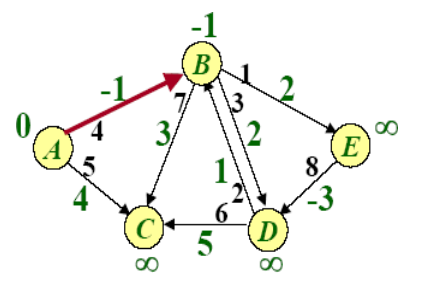
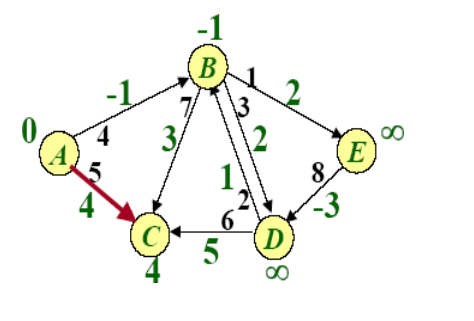



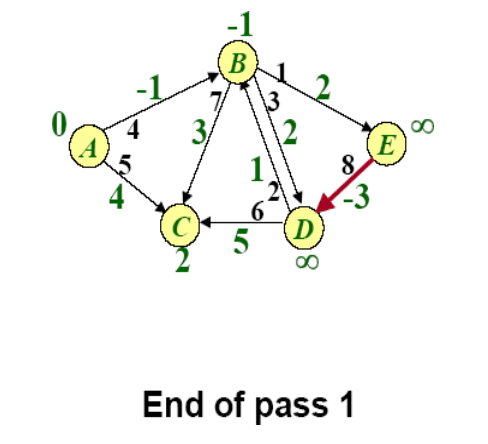
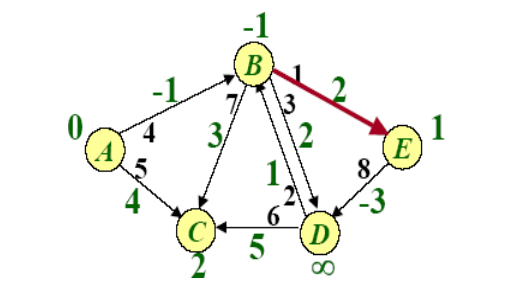
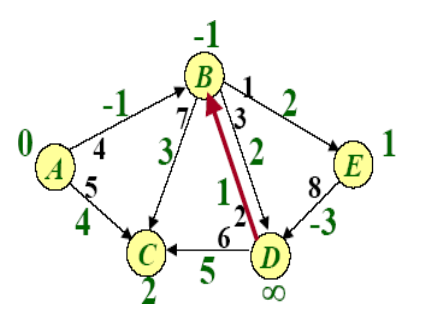
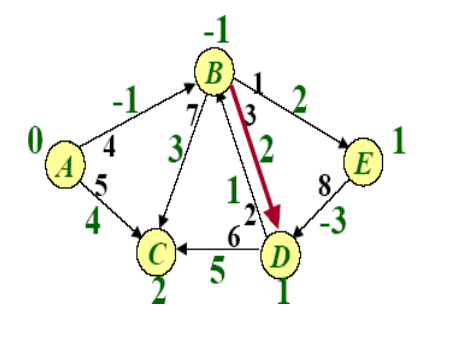
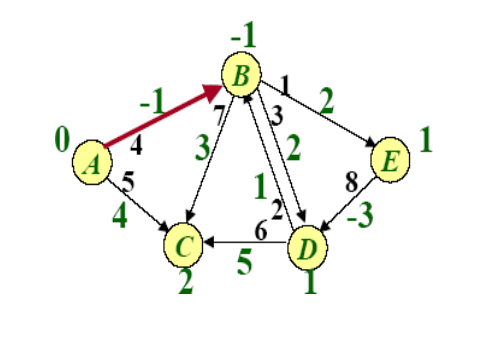
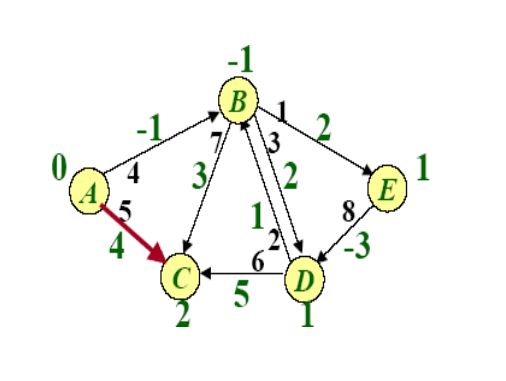
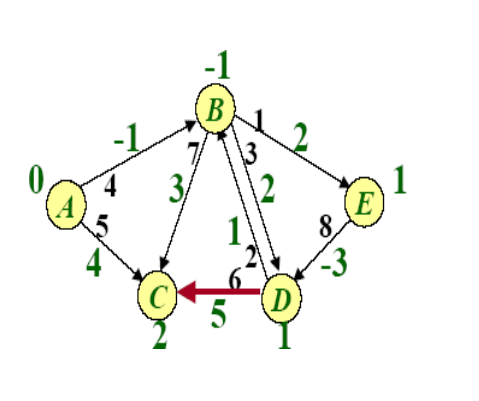

SPFA(Shortest Path Faster Algorithm)
• 在Bellman-Ford算法的基础上用队列优化
• 减少了冗余的松弛操作,是一种高效的最短路算法。
• 维护一个队列,里面存放所有需要进行更新的点。初始时队列中
只有一个源点S(d[s]=0)。每次取出队头的点u, 尝 试 松 弛 u
的 所 有 出 边 <u,v> , 若 能 够 松 弛 d[u]+w[u][v]<d[v], 则改进
d[v]。此时由于s->v的最短距离d[v]变小了,有可能通过v可以改进
其它结点, 将其push进队。这样一直迭代下去直到队列为空,
也就是d[i]都确定下来,结束算法。
• 若一个点最短路被改进的次数达到V(结点数)
• 则说明有负权环(原因同B-F算法)
• 我们可以用spfa算法判断图有无负权环
• SPFA算法时间复杂度的上界为O(VE),同Bellman-Ford算法。
• 记时间为O(kE)
• 在实际情况下中SPFA表现得非常好, k约等于10
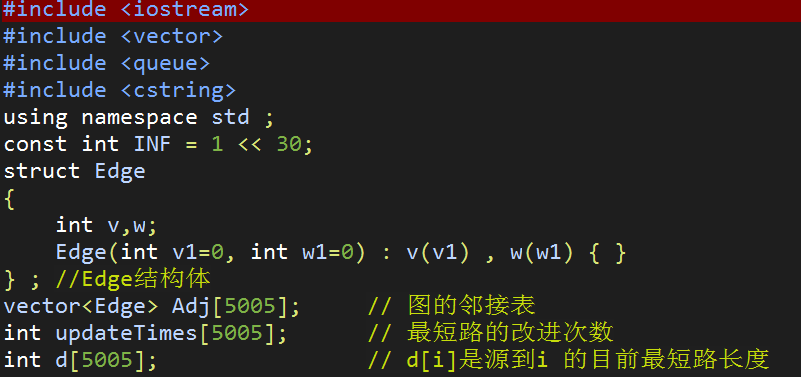

一个好的改进:
可以用一个布尔数组记录每个点是否处在队列中。 若
u不在队列中(通过bool数组判断) 才进行push, 这
样保证队列size不会超过结点数V, 因为每个结点出
现一次。
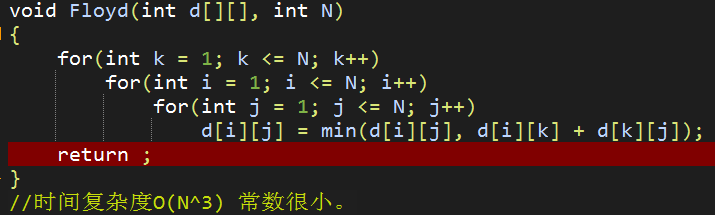
Floyd Algorithm
• 用于求每一对顶点之间的最短路
Dijkstra algorithm
• 从某个源点s到其余各顶点的最短路径, 即单源最短路径(SingleSource Shortest Paths, SSSP) :
• 给定带权图G(V,E)和源点s,求从s到G中其余各顶点的最短路径。
基本思想:
• 1. 设置两个顶点的 集合U 和 集合Q = V-U, U中存放已经确定最短
路径(d值) 的顶点, 集合V-U存放当前还未确定d值的顶点
• 2. 初始状态时, 集合U中只包含源点S;
• 3. 从集合 V-U 中选取d值最小的顶点u加入到U中;
• 4. U中每加入一个顶点u, 都要更新V-U中剩余顶点的d值: dv =
min{dv, du + w(u,v)}; //这一步操作称为“松弛”
• 5. 重复3和4,直到集合U中包含全部顶点。


优先队列(priority_queue)
• 队列(queue):先进先出,队尾入队,队首出队。
• 优先队列(priority_queue):特别之处在于,允许为队列中元素设置
优先级(即保持队列是有序的)。元素入队时,根据其优先级插入
进队列中的相应位置。 STL默认使用“小于 < ”操作符来确定对象之间
的优先级关系, 所以如果要使用自定义优先级, 需要重载‘ < ’操作
符。

自定义优先级
• 类似sort中的自定义cmp函数
• struct Node{ //定义Node结构体
• int d,ind; //
• friend bool operator < (Node n1, Node n2)
• { //重载 ’<’ 操作符,使队列按d值升序排列
• return n1.d > n2.d;
• }
• };
• 对第1种不断更新d值的BFS做4处修改:
1. priority_queue<Node> q;//设置优先队列
2. Node cur=q.top();//队首作为cur
3. 在Node结构体中重载<操作符
4. 当终点Node出队时,可以立即停止并输出d值!
Dijkstra算法的使用条件
• 下面考虑所有边均为非负的情况。在这种情况下, 最短
路是一定存在的, 但最长路却不一定存在。
• Dijkstra算法可用于计算非负权图上的单源最短路(SSSP)。该算
法同时适用于有向图和无向图。
•结点v的d值定义为: 当前从源点v0到v的最短路径长度(其实
是一个不断被更新的上界)
Dijkstra复杂度
• 原版: O(N2)
• 优先队列优化: O(MlogM)
• 稀疏图(M~N):优化版本O(NlogN) < O(N2)
• 稠密图(M~N2): 优化版本O(N2logN) > O(N2)
最短路算法的选择

需要注意的
• 注意:单向/双向(无向)图
• 有没有重边(判负环)和自环
• 有负环时最短路不存在,有正环时最长路不存在。
• 注意图是否可能不连通
EG:
POJ-1201 Intervals
狼抓兔子
路的最小公倍数
最小密度路径
跳棋
墨墨的等式
如果你不开心,那我就把右边 这个帅傻子分享给你吧,
这个帅傻子分享给你吧,
你看,他这么好看,跟个zz一样看着你,你还伤心吗?
真的!这照片盯上他五秒钟就想笑了。
一切都会过去的。
时间时间会给你答案2333