遗传算法求解TSP问题

解题思路

遗传算法步骤：

第一步：初始化 t←0进化代数计数器；T是最大进化代数（也可以没有）；随机生成M个个体作为初始群体P（t）；

第二步：个体评价 计算P（t）中各个个体的适应度；

第三步：选择运算 将选择算子作用于群体；

第四步：交叉运算 将交叉算子作用于群体；

第五步：变异运算 将变异算子作用于群体，并通过以上运算得到下一代群体P（t + 1）;

第六步：终止条件判断 t≦T：t← t+1 转到步骤2；t>T：终止 输出解。

遗传算法求解的一般过程：

1）确定决策变量及各种约束条件，即个体的表现型X和问题的解空间；

2）建立优化模型 （目标函数最大OR 最小） 数学描述形式 量化方法；

3）染色体编码方法；

4）解码方法；

5）个体适应度的量化评价方法 F(x)

6）设计遗传算子；

7）确定有关运行参数。

方法实现

编码方式

应用于TSP问题，选用整数编码，每个整数代表一个城市，一整条路径就是整个染色体编码；如此显式的编码，可以不用解码；

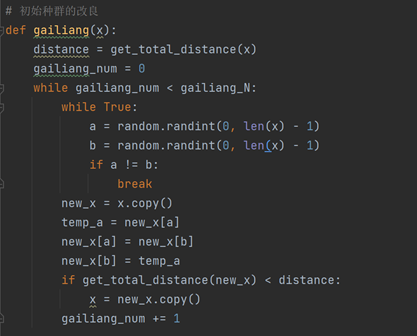
初始种群

随机生成初始种群，并计算这个初始种群的个体适应度。初始化种群时，采用改良版本，为了初始化一个较好的种群，如果随即交换两个城市的位置，如果总距离减小，那么就更新这个染色体。

选择算子

选择总距离作为适应度函数，距离越小适应度越高，（存活率与总距离的倒数成正比）

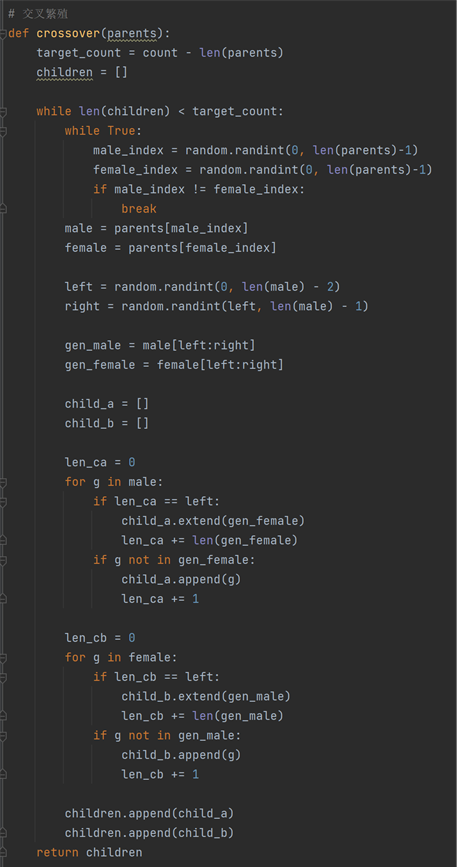
交叉算子

1 部分映射交叉

选择交换部分，交换父代个体基因产生子代，然后建立映射表，根据映射表来消除基因冲突。

2 顺序交叉

在父代样本1中选择交换部分，根据父代1的交叉部分先生成子代1的部分基因片段，然后将父代2中未被选中的基因按顺序复制到子代1的空余部分；然后根据父代2选择交叉部分生成子代2，并将父代1中未选择的部分复制到子代2的空余；

3 基于位置的交叉

在父代1选择时随机选择需要交换的基因，根据交叉部分生成子代1；将父代2中未被选择到的基因复制到子代1中；然后根据父代2随机选择交叉部分生成子代2，并将父代1中未选择的部分复制到子代2的空余；

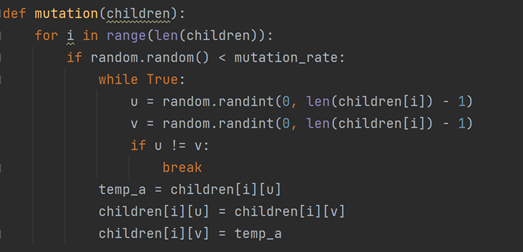
变异算子

根据变异算子的概率，变异时随机选择两个不同的位置的基因进行交换。也可以采用三点变异法，随机生成abc三点，将ac基因片段与bc做交换。

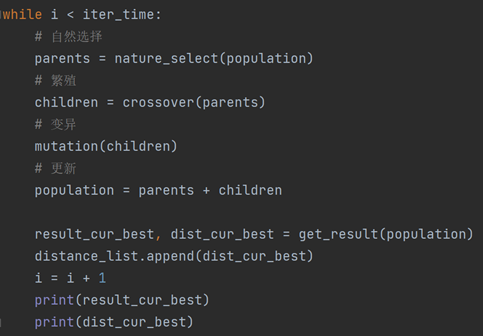
更新种群

采用杰出父代+子代的方式来更新种群。

我在求解时采用了在初始种群中进行改良的方法，收敛速度相对变快，求解与标准结果。完全正确

求解结果

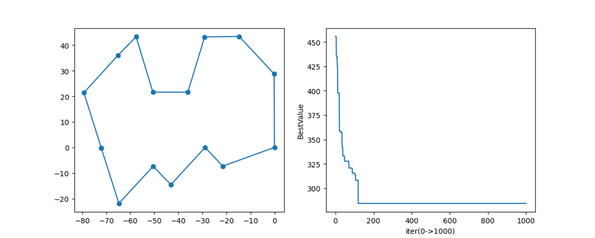
距离和城市序列

TSP图和Loss

实现代码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
import math
import random

# 处理数据
coord = []
with open("p_xy.txt", "r") as lines:
    lines = lines.readlines()
    for line in lines:
        xy = line.split()
        coord.append(xy)

coord = np.array(coord)
w, h = coord.shape
coordinates = np.zeros((w, h), float)
for i in range(w):
    for j in range(h):
        coordinates[i, j] = float(coord[i, j])
# print(coordinates)

# 得到距离矩阵
distance = np.zeros((w, w))
for i in range(w):
    for j in range(w):
        distance[i, j] = distance[j, i] = np.linalg.norm(coordinates[i] - coordinates[j])

# 种群数
count = 300
# 进化次数
iter_time = 1000
# 最优选择概率
retain_rate = 0.3  # 适应度前30%可以活下来
# 弱者生存概率
random_select_rate = 0.5
# 变异
mutation_rate = 0.1
# 改良
gailiang_N = 3000


# 适应度
def get_total_distance(x):
    dista = 0
    for i in range(len(x)):
        if i == len(x) - 1:
            dista += distance[x[i]][x[0]]
        else:
            dista += distance[x[i]][x[i + 1]]
    return dista


# 初始种群的改良
def gailiang(x):
    distance = get_total_distance(x)
    gailiang_num = 0
    while gailiang_num < gailiang_N:
        while True:
            a = random.randint(0, len(x) - 1)
            b = random.randint(0, len(x) - 1)
            if a != b:
                break
        new_x = x.copy()
        temp_a = new_x[a]
        new_x[a] = new_x[b]
        new_x[b] = temp_a
        if get_total_distance(new_x) < distance:
            x = new_x.copy()
        gailiang_num += 1


# 自然选择
def nature_select(population):
    grad = [[x, get_total_distance(x)] for x in population]
    grad = [x[0] for x in sorted(grad, key=lambda x: x[1])]
    # 强者
    retain_length = int(retain_rate * len(grad))
    parents = grad[: retain_length]
    # 生存下来的弱者
    for ruozhe in grad[retain_length:]:
        if random.random() < random_select_rate:
            parents.append(ruozhe)
    return parents


# 交叉繁殖
def crossover(parents):
    target_count = count - len(parents)
    children = []

    while len(children) < target_count:
        while True:
            male_index = random.randint(0, len(parents)-1)
            female_index = random.randint(0, len(parents)-1)
            if male_index != female_index:
                break
        male = parents[male_index]
        female = parents[female_index]

        left = random.randint(0, len(male) - 2)
        right = random.randint(left, len(male) - 1)

        gen_male = male[left:right]
        gen_female = female[left:right]

        child_a = []
        child_b = []

        len_ca = 0
        for g in male:
            if len_ca == left:
                child_a.extend(gen_female)
                len_ca += len(gen_female)
            if g not in gen_female:
                child_a.append(g)
                len_ca += 1

        len_cb = 0
        for g in female:
            if len_cb == left:
                child_b.extend(gen_male)
                len_cb += len(gen_male)
            if g not in gen_male:
                child_b.append(g)
                len_cb += 1

        children.append(child_a)
        children.append(child_b)
    return children


def mutation(children):
    for i in range(len(children)):
        if random.random() < mutation_rate:
            while True:
                u = random.randint(0, len(children[i]) - 1)
                v = random.randint(0, len(children[i]) - 1)
                if u != v:
                    break
            temp_a = children[i][u]
            children[i][u] = children[i][v]
            children[i][v] = temp_a


def get_result(population):
    grad = [[x, get_total_distance(x)] for x in population]
    grad = sorted(grad, key=lambda x: x[1])
    return grad[0][0], grad[0][1]


population = []
# 初始化种群
index = [i for i in range(w)]
for i in range(count):
    x = index.copy()
    random.shuffle(x)
    gailiang(x)
    population.append(x)

distance_list = []
result_cur_best, dist_cur_best = get_result(population)
distance_list.append(dist_cur_best)

i = 0
while i < iter_time:
    # 自然选择
    parents = nature_select(population)
    # 繁殖
    children = crossover(parents)
    # 变异
    mutation(children)
    # 更新
    population = parents + children

    result_cur_best, dist_cur_best = get_result(population)
    distance_list.append(dist_cur_best)
    i = i + 1
    print(result_cur_best)
    print(dist_cur_best)


for i in range(len(result_cur_best)):
    result_cur_best[i] += 1

result_path = result_cur_best
result_path.append(result_path[0])

print(result_path)

# 画图
X = []
Y = []
for index in result_path:
    X.append(coordinates[index-1, 0])
    Y.append(coordinates[index-1, 1])

plt.figure(figsize=(20, 20))

plt.subplot(1, 2, 1)
plt.plot(X, Y, '-o')
# plt.set_title("GA_TSP")

plt.subplot(1, 2, 2)
plt.plot(np.array(distance_list))
# plt.set_title("GA_TSPLoss")
plt.ylabel("BestValue")
plt.xlabel("iter({}->{})".format(0, iter_time))
plt.show()