最小生成树求解TSP问题
步骤:
首先根据输入生成TSP地图数据,然后利用克鲁斯卡尔(Kruskal)和普利姆(prim)算法求解这个TSP问题,最后用图画出来。
算法思想:
克鲁斯卡尔算法的核心思想是:在带权连通图中,不断地在边集合中找到最小的边,如果该边满足得到最小生成树的条件,就将其构造,直到最后得到一颗最小生成树
普利姆算法的核心步骤是:在带权连通图中,从图中某一顶点v开始,此时集合U={v},重复执行下述操作:在所有u∈U,w∈V-U的边(u,w)∈E中找到一条权值最小的边,将(u,w)这条边加入到已找到边的集合,并且将点w加入到集合U中,当U=V时,就找到了这颗最小生成树。
算法代码(python)
Kruskal
# kruskal
edge_count = 0
for i in range(size):
for j in range(i):
if 0 < distance[i][j] < 999998:
edge_count += 1
kruskal_list = []
edge_list = []
for i in range(size):
for j in range(i+1, size):
edge_list.append([i, j, distance[i][j]])
edge_list.sort(key=lambda a: a[2])
group = [[i] for i in range(size)]
for edge in edge_list:
for i in range(len(group)):
if edge[0] in group[i]:
m = i
if edge[1] in group[i]:
n = i
if m != n:
kruskal_list.append(edge)
group[m] = group[m] + group[n]
group[n] = []
Prim
# Prim
prim_list = []
selected_node = [0]
candidate_node = [i for i in range(1, size)]
while len(candidate_node) > 0 :
min_dis = 999998
for i in selected_node:
for j in candidate_node:
if distance[i][j] < min_dis:
min_dis = distance[i][j]
cur_node = i
next_select_node = j
prim_list.append([cur_node, next_select_node, min_dis])
selected_node.append(next_select_node)
candidate_node.remove(next_select_node)
代码测试:
(1)
15个城市迅速收敛
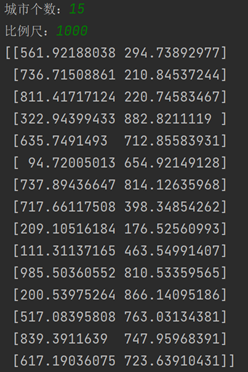
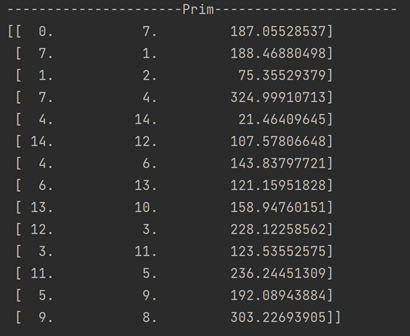
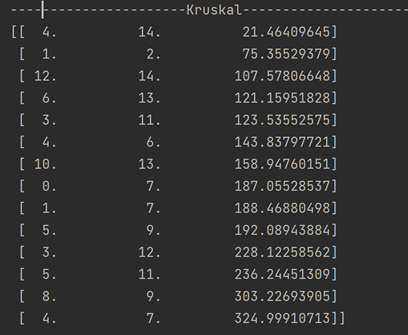
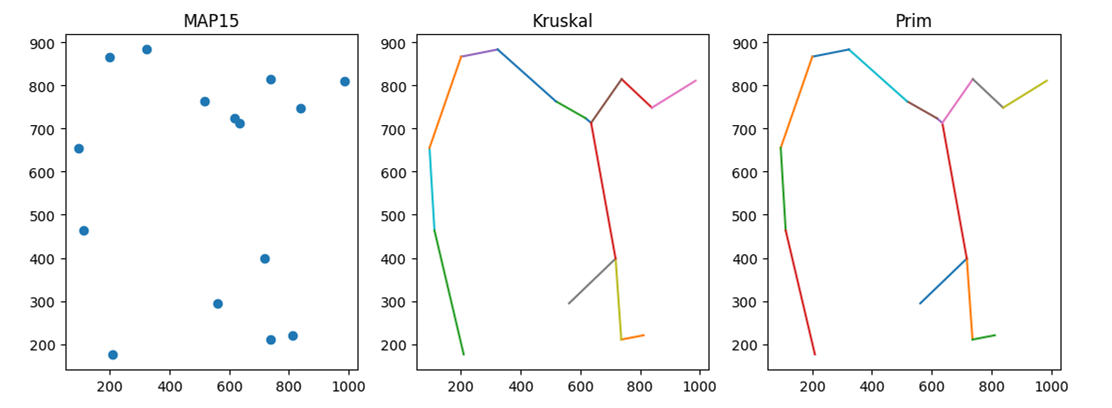
(2)
100个城市可以快速收敛
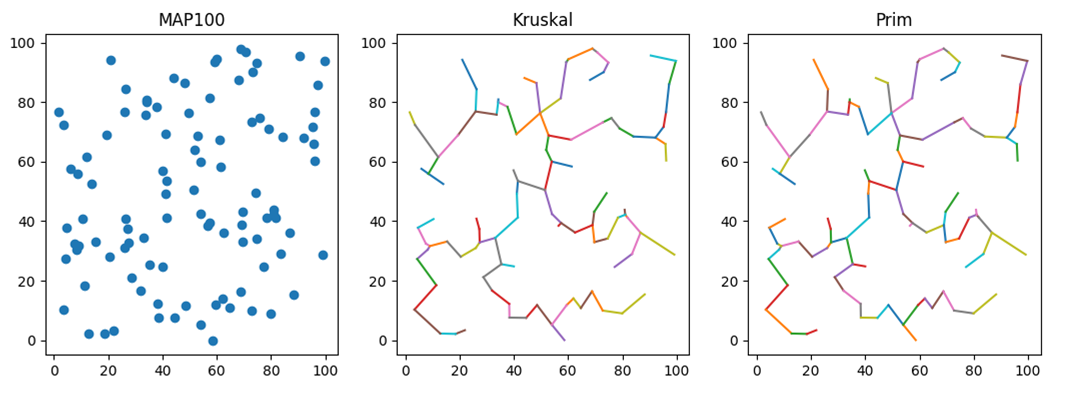
(3)
1000个城市无法快速收敛
源代码:
import numpy as np
import matplotlib.pyplot as plt
size = int(input("城市个数:"))
scale = int(input("比例尺:"))
MAX_ = 999999
coord = []
distance = np.zeros((size, size))
i = 0
while i < size:
x = np.random.rand() * scale
y = np.random.rand() * scale
if [x, y] not in coord:
coord.append([x, y])
i = i + 1
coord = np.array(coord)
for i in range(size):
for j in range(size):
if i == j :
distance[i][j] = MAX_
else:
distance[i][j] = distance[j][i] = np.linalg.norm(coord[i] - coord[j])
# kruskal
edge_count = 0
for i in range(size):
for j in range(i):
if 0 < distance[i][j] < 999998:
edge_count += 1
kruskal_list = []
edge_list = []
for i in range(size):
for j in range(i+1, size):
edge_list.append([i, j, distance[i][j]])
edge_list.sort(key=lambda a: a[2])
group = [[i] for i in range(size)]
for edge in edge_list:
for i in range(len(group)):
if edge[0] in group[i]:
m = i
if edge[1] in group[i]:
n = i
if m != n:
kruskal_list.append(edge)
group[m] = group[m] + group[n]
group[n] = []
# Prim
prim_list = []
selected_node = [0]
candidate_node = [i for i in range(1, size)]
while len(candidate_node) > 0 :
min_dis = 999998
for i in selected_node:
for j in candidate_node:
if distance[i][j] < min_dis:
min_dis = distance[i][j]
cur_node = i
next_select_node = j
prim_list.append([cur_node, next_select_node, min_dis])
selected_node.append(next_select_node)
candidate_node.remove(next_select_node)
print(coord)
print(distance)
print("----------------------Kruskal-----------------------")
print(np.array(kruskal_list))
print("----------------------Prim-----------------------")
print(np.array(prim_list))
fig = plt.figure(1, (45, 15))
ax1 = fig.add_subplot(131)
ax1.set_title("MAP{}".format(size))
ax1.plot(coord[:, 0], coord[:, 1], 'o')
ax2 = fig.add_subplot(132)
ax2.set_title("Kruskal")
x = []
y = []
for t_list in kruskal_list:
ax2.plot([coord[t_list[0], 0], coord[t_list[1], 0]], [coord[t_list[0], 1], coord[t_list[1], 1]])
ax3 = fig.add_subplot(133)
ax3.set_title("Prim")
for t_list in prim_list:
ax3.plot([coord[t_list[0], 0], coord[t_list[1], 0]], [coord[t_list[0], 1], coord[t_list[1], 1]])
plt.show()