牛客IOI周赛20-普及组
完全数
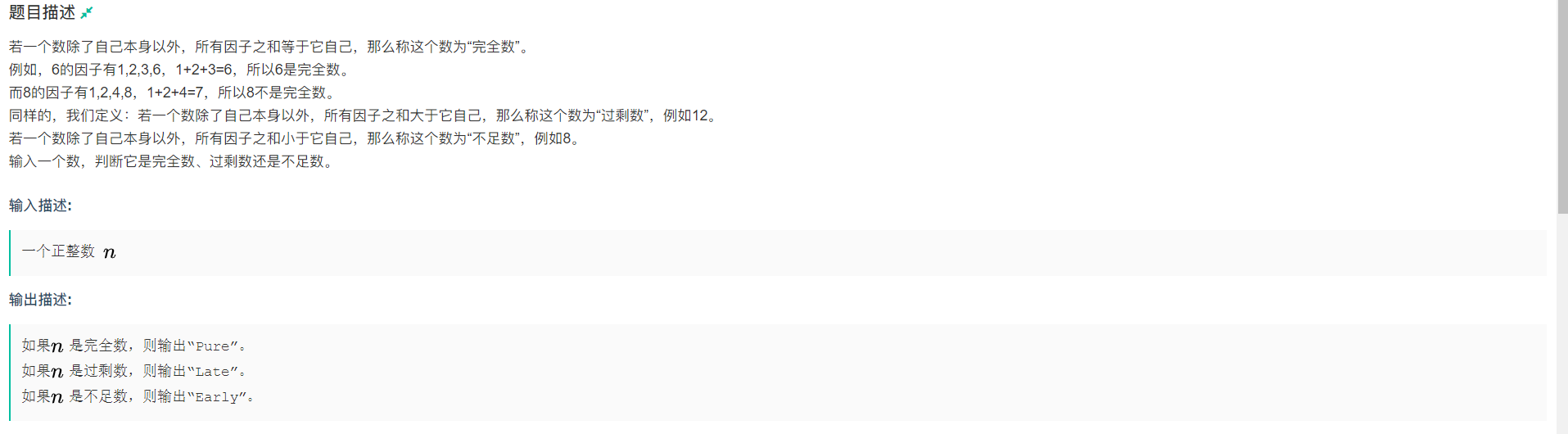
牛客的签到题,最暴力的做法就是把数每个因子罗列出来,但是这样只有60的暴力分,我们从题目的数据可以看到
数据范围是1e7的,在学习素数的时候我们知道一个因子就能推出另一个因子,所以我们没必要从1判断到n-1
直接i*i <= n就能找到所有的因子,但是注意像16这样的数,当我们的i为4的时候,这个4的因子只能算一次
Code:
#include<bits/stdc++.h>
using namespace std;
int main()
{
long long n;
scanf("%lld",&n);
long long sum = 1;
for(long long i = 2; i * i <= n; ++i) {
if(n % i == 0)
sum += n/i == i? 0 : n/i + i ;//判断是否是重因子
}
if(sum > n) {
puts("Late");
} else if(sum == n) {
puts("Pure");
} else if(sum < n) {
puts("Early");
}
return 0;
}
移动撤销

解题思路:这个题是一个模拟题,我们先记录牛牛的操作,然后在记录的时候每次遇到Z,就把上一个操作删掉
最后直接按照没有Z的操作模拟,然后输出最终的坐标,注意这里的Z,可能Z的上一个位置没有任何操作,用栈的同学请注意空栈的情况
Code:
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n;
vector<char> V;
char c;
cin >> n;
for(int i = 0; i < n; ++i) {
cin>>c;
if(c == 'Z') {
if(V.size())//当V不为空的时候才进行撤销操作
V.pop_back();
} else {
V.push_back(c);
}
}
int x,y;
x = y = 0;
for(int i = 0; i < V.size(); ++i) {//直接模拟
if(V[i] == 'W') {
y++;
} else if(V[i] == 'A') {
x--;
} else if(V[i] == 'S') {
y--;
} else if(V[i] == 'D') {
x++;
}
}
cout << x << " " << y << endl;//最后输出x和y
return 0;
}
石头剪刀布

解题思路:牛牛要想分数拿的高,那么就要尽可能的不输,我们可以计算牛牛最多能赢的场数,然后再把赢的场数从游戏场数剪掉
然后再计算平局可能的场数就是最高的分数,然后……然后就AC了呀
Code:
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin>>n;
int a1,b1,c1;
int a2,b2,c2;
cin>>a1>>b1>>c1;
cin>>a2>>b2>>c2;
int win1,win2,win3;//这是牛牛可能会赢的场数(分别对应着石头、剪刀、布)
long long sum = 0;
win1 = min(a1,b2);
win2 = min(b1,c2);
win3 = min(c1,a2);
sum += win1 * 2;
sum += win2 * 2;
sum += win3 * 2;
a1 -= win1;//这里分别减去牛牛赢的场数
b2 -= win1;
b1 -= win2;
c2 -= win2;
c1 -= win3;
a2 -= win3;
sum += min(a1,a2) + min(b1,b2) + min(c1,c2);//最后再把可能平局的场数加起来就好啦
cout<<sum<<endl;
return 0;
}
夹缝中求和

解题思路:我们要求范围在X和Y之间的不同数的两两组合,且i<j,很明显数的位置不重要,我们就可以队数组进行排序操作
然后我们枚举i,找到满足条件的aj的范围,aj的范围是X到Y的,所以我们可以用二分查询找到j的范围(因为前面排过序了)
Code:
#include<bits/stdc++.h>
using namespace std;
const int N = 100005;
int a[N];
int find(int l,int r,int key)
{
while(l+1<r)
{
int mid=l+r>>1;
if(a[mid]<=key)
l=mid;
else
r=mid;
}
return r;
}
int main()
{
int n,x,y;
scanf("%d%d%d",&n,&x,&y);
for(int i = 0;i < n; ++i) {
scanf("%d",&a[i]);
}
long long sum = 0;
sort(a,a+n);
for(int i = 0;i < n; ++i) {
int k1 = x - a[i];
int k2 = y - a[i];
int loc1 = max(i+1,find(-1,n,k1 - 1));//找到满足条件的左边的位置
int loc2 = max(loc1,find(-1,n,k2));//右边的位置
sum += max(0,loc2 - loc1);
}
printf("%lld
",sum);
return 0;
}
当然这题还能用双指针做,但是不知道为什么我的双指针写出来炸了,然后写了个'单指针'?hh
如果但看这个左边界或者有边界的话,我们可以直接写出一个0(N)的操作,然后我们会发现这样写的话会有值的重叠
所以我们直接把考虑右边界的情况减去左边界的情况就OK啦,不懂的话可以手算一下哦
Code
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 100005;
int a[N];
int main()
{
int n,x,y;
scanf("%d%d%d",&n,&x,&y);
for(int i = 0;i < n; ++i) {
scanf("%d",&a[i]);
}
sort(a,a+n);
int l = 0, r = 0;
long long sum = 0;
for(int i = 0, j = n - 1 ;i < n; ++i) {//计算的是只考虑有边界的情况
while(j > 0 && a[i] + a[j] > y) j--;
if(j < i) break;
sum += j - i;
}
for(int i = 0, j = n - 1 ;i < n; ++i) {//计算的是只考虑左边界的情况
while(j > 0 && a[i] + a[j] >= x) j--;
if(j < i) break;
sum -= j - i;
}
printf("%lld
",sum);
}
第一次AK,++rp;