POJ 2559 Largest Rectangle in a Histogram

Description

A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles: 

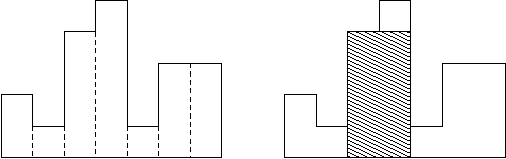
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

Input

The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1<=n<=100000. Then follow n integers h₁,...,h_n, where 0<=h_i<=1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.

Output

For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.

Sample Input

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

 

Sample output

8

4000

翻译

柱状图是一个多边形，由一系列在公共基线上对齐的矩形组成。矩形的宽度相等，但高度不同。例如，左侧的图显示了由高度为2、1、4、5、1、3、3的矩形组成的直方图，以单位度量，其中1是矩形的宽度：
通常，柱状图用于表示离散分布，例如文本中字符的频率。请注意，矩形的顺序，即它们的高度，非常重要。计算柱状图中最大矩形的面积，该柱状图也与公共基线对齐。右图显示了所示直方图的最大对齐矩形。
输入
输入包含几个测试用例。每个测试用例描述一个柱状图，以一个整数n开头，表示它所组成的矩形的数量。您可以假设1<=n<=100000。然后跟随n个整数h1，…，hn，其中0<=hi<=100000000。这些数字表示从左到右的柱状图矩形的高度。每个矩形的宽度为1。最后一个测试用例的输入后面跟着一个零。
输出
对于单行上的每个测试用例输出，指定柱状图中最大矩形的面积。记住，这个矩形必须与公共基线对齐。

分析

这道题网上大多是用单调栈，然而我觉得这道题用单调队列和单调栈都是一样的

这个矩形肯定是以某一个为基准向两边扩展的

我们可以对某一个柱子的高度为标准，尽量的向两头扩展，这样就可以找出以它高度为标准的，并包含它本身的最大矩形。然后对每一个柱子都做类似的工作，最后挑出里面最大的矩形。

有没有跟动规里面最大子矩阵的一个方法很像？

最后注意细节

代码

/************************
User:Mandy.H.Y
Language:c++
Problem:POj 2559
Algorithm： 
************************/
//#include<bits/stdc++.h>
#include<cstdio>
#include<iomanip> 
#include<cmath> 

using namespace std;

const int maxn = 1e5 + 5;

int n,l,r;
int q[maxn];

struct Node{
    int h,l,r;
}node[maxn]; 

template<class T>inline void read(T &x){
    x = 0;bool flag = 0;char ch = getchar();
    while(!isdigit(ch)) flag |= ch == '-',ch =  getchar();
    while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch =  getchar();
    if(flag) x = -x;
}

template<class T>void putch(const T x){
    if(x > 9) putch(x / 10);
    putchar(x % 10 | 48);
}

template<class T>void put(const T x){
    if(x < 0) putchar('-'),putch(-x);
    else putch(x);
}

void file(){
    freopen("2559.in","r",stdin);
//    freopen("1090.out","r",stdin);
}

void work(){
    read(n);
    while(n){
        long long ans = 0;
        for(int i = 1;i <= n; ++ i) read(node[i].h),node[i].l = i,node[i].r = i;
        //初始化l，r 
        l = r = 0;
        for(int i = 1;i <= n; ++ i){
            while(l < r && node[q[r - 1]].h >= node[i].h) node[i].l = node[q[r - 1]].l,r--;
            //q中存的是编号，更新时 node[i].l = node[q[r - 1]].l，也可以是剩下的那个坐标 +1，但是要判空 
            q[r++] = i;
        }
        l = r = 0;
        for(int i = n; i >= 1; -- i){
            while(l < r && node[q[r - 1]].h >= node[i].h) node[i].r = node[q[r - 1]].r,r--;
            q[r++] = i;
            ans = max(ans,(long long)node[i].h * (node[i].r - node[i].l + 1));
        }
        put(ans);
        putchar('
');
        read(n);
    }
}

int main(){
//    file();
    work();
    return 0;
}