Codeforces Round #590 (Div. 3) C——1234C Pipes

D. Distinct Characters Queries

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a system of pipes. It consists of two rows, each row consists of nn pipes. The top left pipe has the coordinates (1,1)(1,1) and the bottom right — (2,n)(2,n).

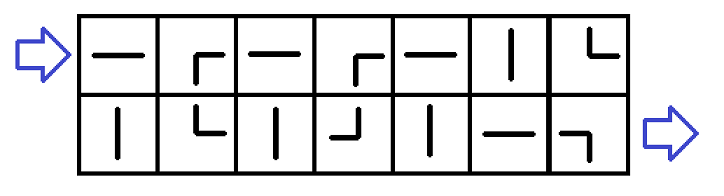
There are six types of pipes: two types of straight pipes and four types of curved pipes. Here are the examples of all six types:

Types of pipes

You can turn each of the given pipes 9090 degrees clockwise or counterclockwise arbitrary (possibly, zero) number of times (so the types 11 and 22 can become each other and types 3,4,5,63,4,5,6 can become each other).

You want to turn some pipes in a way that the water flow can start at (1,0)(1,0) (to the left of the top left pipe), move to the pipe at (1,1)(1,1), flow somehow by connected pipes to the pipe at (2,n)(2,n) and flow right to (2,n+1)(2,n+1).

Pipes are connected if they are adjacent in the system and their ends are connected. Here are examples of connected pipes:

Examples of connected pipes

Let's describe the problem using some example:

The first example input

And its solution is below:

The first example answer

As you can see, the water flow is the poorly drawn blue line. To obtain the answer, we need to turn the pipe at (1,2)(1,2) 9090 degrees clockwise, the pipe at (2,3)(2,3) 9090 degrees, the pipe at (1,6)(1,6) 9090 degrees, the pipe at (1,7)(1,7) 180180 degrees and the pipe at (2,7)(2,7) 180180 degrees. Then the flow of water can reach (2,n+1)(2,n+1) from (1,0)(1,0).

You have to answer qq independent queries.

Input

The first line of the input contains one integer qq (1≤q≤1041≤q≤104) — the number of queries. Then qq queries follow.

Each query consists of exactly three lines. The first line of the query contains one integer nn (1≤n≤2⋅1051≤n≤2⋅105) — the number of pipes in each row. The next two lines contain a description of the first and the second rows correspondingly. Each row description consists of nndigits from 11 to 66 without any whitespaces between them, each digit corresponds to the type of pipe in the corresponding cell. See the problem statement to understand which digits correspond to which types of pipes.

It is guaranteed that the sum of nn over all queries does not exceed 2⋅1052⋅105.

Output

For the ii-th query print the answer for it — "YES" (without quotes) if it is possible to turn some pipes in a way that the water flow can reach (2,n+1)(2,n+1) from (1,0)(1,0), and "NO" otherwise.

Example

input

Copy

6
7
2323216
1615124
1
3
4
2
13
24
2
12
34
3
536
345
2
46
54

output

Copy

YES
YES
YES
NO
YES
NO

Note

The first query from the example is described in the problem statement.

 

题目大意：给两行可以旋转的水管，给了六个原型，但是通过旋转可以互相转换，所以实际上只有两种水管，然后判断能不能从左上角走到右上角，同时保证右下角的水管是对着右边的（仔细读题，我就被这个坑惨了）

这个有点像一个4399的小游戏，刚看完题有点懵，想了想发现题目看上去有点吓人，但是其实是个纸老虎，因为水管的流向没什么操作的空间，因为题目要求是从左上角到右下角，那么就不用考虑往左的情况的了，竖着的水管也是不用考虑的，这样就只有2,3,4,6是要考虑的，把每种情况都讨论一下，dfs走的时候记录一下上一根管子的流向结合当前管道的横纵坐标就可以判断当前是哪种管道从而继续dfs了。

代码如下：

#include<bits/stdc++.h>
#include<vector>
#include<map>
#include<queue>
#define LL long long
#define INF 0x3f3f3f3f
#define MOD 1000000007
using namespace std;
char s[4][200005];
int vis[4][200005];
int q, n, flag;
void dfs(int x, int y, int t)                //x，y代表横纵坐标，t代表上一根管道的流向
{
     if(x == 2 && y == n && t == 4)           //判断条件
     {
         flag = 1;
         return;
     }
     if(y > (n+5))                            //过界时return
         return;
     if(s[x][y] >= '3')
     {
         if(t == 0 || (t == 4 && x == 1))     //此时为4号管道
         {
             //printf("1 lujin
");
             dfs(x+1, y, 2);                
         }
         else if(t == 1 && x == 1)            //此时为3号管道
         {
             //printf("2 lujin
");
             dfs(x, y+1, 4);
         }
         else if(x == 2 && t == 4)            //此时为5号管道
         {
           //printf("3 lujin
");
             dfs(x-1, y, 1);
         }
         else if(t == 2 && x == 2)            //此时为六号管道
         {
             //printf("4 lujin
");
             dfs(x, y+1, 4);
         }
     }
     else
     {
         if(t == 4 || t == 0)                  //横竖管道只能转成横管道向右走
         {
             //printf("6 lujin
");
             dfs(x, y+1, 4);
         }
         else
         return;
     }
}
int main()
{
     scanf("%d", &q);
     while(q--)
     {
         flag = 0;
         scanf("%d", &n);
         for(int i = 1;i <= 2;i++)
         cin>>s[i];
         dfs(1, 0, 0);              //从左上角开始dfs
         if(flag)
             printf("YES
");
         else
             printf("NO
");

     }
     return 0;
}

C. PipesYou are given a system of pipes. It consists of two rows, each row consists of n pipes. The top left pipe has the coordinates (1,1) and the bottom right — (2,n).
There are six types of pipes: two types of straight pipes and four types of curved pipes. Here are the examples of all six types:

You can turn each of the given pipes 90 degrees clockwise or counterclockwise arbitrary (possibly, zero) number of times (so the types 1 and 2 can become each other and types 3,4,5,6 can become each other).
You want to turn some pipes in a way that the water flow can start at (1,0) (to the left of the top left pipe), move to the pipe at (1,1), flow somehow by connected pipes to the pipe at (2,n) and flow right to (2,n+1).
Pipes are connected if they are adjacent in the system and their ends are connected. Here are examples of connected pipes:

Examples of connected pipesLet’s describe the problem using some example:
The first example input

And its solution is below:

The first example answerAs you can see, the water flow is the poorly drawn blue line. To obtain the answer, we need to turn the pipe at (1,2) 90 degrees clockwise, the pipe at (2,3) 90 degrees, the pipe at (1,6) 90 degrees, the pipe at (1,7) 180 degrees and the pipe at (2,7) 180 degrees. Then the flow of water can reach (2,n+1) from (1,0).
You have to answer q independent queries.
InputThe first line of the input contains one integer q (1≤q≤104) — the number of queries. Then q queries follow.
Each query consists of exactly three lines. The first line of the query contains one integer n (1≤n≤2⋅105) — the number of pipes in each row. The next two lines contain a description of the first and the second rows correspondingly. Each row description consists of n digits from 1 to 6 without any whitespaces between them, each digit corresponds to the type of pipe in the corresponding cell. See the problem statement to understand which digits correspond to which types of pipes.
It is guaranteed that the sum of n over all queries does not exceed 2⋅105.
OutputFor the i-th query print the answer for it — “YES” (without quotes) if it is possible to turn some pipes in a way that the water flow can reach (2,n+1) from (1,0), and “NO” otherwise.————————————————版权声明：本文为CSDN博主「Herod_」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。原文链接：https://blog.csdn.net/qq_43461168/article/details/101981692