关联规则挖掘：Apriori算法（基于Groceries数据集）

在美国有这样一家奇怪的超市，它将啤酒与尿布这样两个奇怪的东西放在一起进行销售，并且最终让啤酒与尿布这两个看起来没有关联的东西的销量双双增加。这家超市的名字叫做沃尔玛。

你会不会觉得有些不可思议？虽然事后证明这个案例确实有根据，美国的太太们常叮嘱她们的丈夫下班后为小孩买尿布，而丈夫们在买尿布后又随手带回了他们喜欢的啤酒。但这毕竟是事后分析，我们更应该关注的，是在这样的场景下，如何找出物品之间的关联规则。接下来就来介绍下如何使用Apriori算法，来找到物品之间的关联规则吧。

一. 关联分析概述

选择物品间的关联规则也就是要寻找物品之间的潜在关系。要寻找这种关系，有两步，以超市为例

找出频繁一起出现的物品集的集合，我们称之为频繁项集。比如一个超市的频繁项集可能有{{啤酒,尿布},{鸡蛋,牛奶},{香蕉,苹果}}
在频繁项集的基础上，使用关联规则算法找出其中物品的关联结果。
简单点说，就是先找频繁项集，再根据关联规则找关联物品。

为什么要先找频繁项集呢？还是以超市为例，你想想啊，我们找物品关联规则的目的是什么，是为了提高物品的销售额。如果一个物品本身购买的人就不多，那么你再怎么提升，它也不会高到哪去。所以从效率和价值的角度来说，肯定是优先找出那些人们频繁购买的物品的关联物品。

既然要找出物品的关联规则有两步，那我们也一步一步来。我们会先介绍如何用Apriori找出物品的频繁项集，然后下一篇会在Apriori处理后的频繁项集的基础上，进行物品的关联分析。

二. Apriori算法基础概念

在介绍Apriori算法之前，我们需要先了解几个概念，别担心，我们会结合下面的例子来进行说明的。

这些是一个超市里面的一部分购买商品记录：

交易编号 购买商品
0 牛奶,洋葱,肉豆蔻,芸豆,鸡蛋,酸奶
1 莳萝,洋葱,肉豆蔻,芸豆,鸡蛋,酸奶
2 牛奶,苹果,芸豆,鸡蛋
3 牛奶,独角兽,玉米,芸豆,酸奶
4 玉米,洋葱,洋葱,芸豆,冰淇淋,鸡蛋

2.1 关联分析的几个概念

支持度（Support）：支持度可以理解为物品当前流行程度。计算方式是：

支持度 = （包含物品A的记录数量） / （总的记录数量）

用上面的超市记录举例，一共有五个交易，牛奶出现在三个交易中，故而{牛奶}的支持度为3/5。{鸡蛋}的支持度是4/5。牛奶和鸡蛋同时出现的次数是2，故而{牛奶，鸡蛋}的支持度为2/5。

置信度（Confidence）：置信度是指如果购买物品A，有较大可能购买物品B。计算方式是这样：

置信度( A -> B) = （包含物品A和B的记录数量） / （包含 A 的记录数量）

举例：我们已经知道，(牛奶，鸡蛋)一起购买的次数是两次，鸡蛋的购买次数是4次。那么Confidence(牛奶->鸡蛋)的计算方式是Confidence(牛奶->鸡蛋)=2 / 4。

提升度（Lift）：提升度指当销售一个物品时，另一个物品销售率会增加多少。计算方式是：

提升度( A -> B) = 置信度( A -> B) / (支持度 A)

举例：上面我们计算了牛奶和鸡蛋的置信度Confidence(牛奶->鸡蛋)=2 / 4。牛奶的支持度Support(牛奶)=3 / 5，那么我们就能计算牛奶和鸡蛋的支持度Lift(牛奶->鸡蛋)=0.83
当提升度(A->B)的值大于1的时候，说明物品A卖得越多，B也会卖得越多。而提升度等于1则意味着产品A和B之间没有关联。最后，提升度小于1那么意味着购买A反而会减少B的销量。

其中支持度和Apriori相关，而置信度和提升度是下一篇寻找物品关联规则的时候会用到。

2.2 Apriori 算法介绍

Apriori的作用是根据物品间的支持度找出物品中的频繁项集。通过上面我们知道，支持度越高，说明物品越受欢迎。那么支持度怎么决定呢？这个是我们主观决定的，我们会给Apriori提供一个最小支持度参数，然后Apriori会返回比这个最小支持度高的那些频繁项集。

说到这里，有人可能会发现，既然都知道了支持度的计算公式，那直接遍历所有组合计算它们的支持度不就可以了吗？

是的，没错。确实可以通过遍历所有组合就能找出所有频繁项集。但问题是遍历所有组合花的时间太多，效率太低，假设有N个物品，那么一共需要计算2^N-1次。每增加一个物品，数量级是成指数增长。而Apriori就是一种找出频繁项集的高效算法。它的核心就是下面这句话：

某个项集是频繁的，那么它的所有子集也是频繁的。

这句话看起来是没什么用，但是反过来就很有用了。

如果一个项集是 非频繁项集，那么它的所有超集也是非频繁项集。

Apriori算法中的非频繁项集:

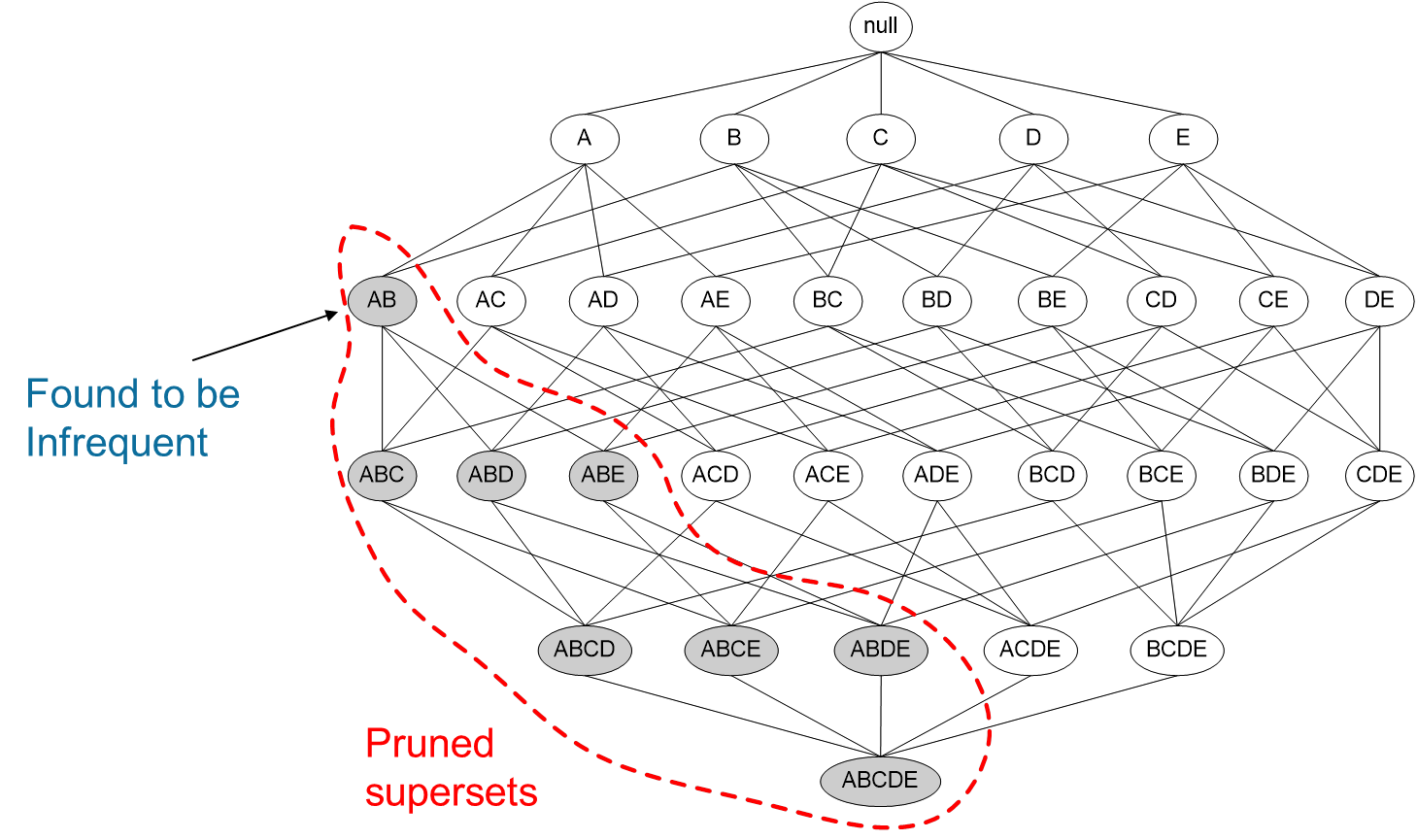
如图所示，我们发现{A,B}这个项集是非频繁的，那么{A,B}这个项集的超集，{A,B,C},{A,B,D}等等也都是非频繁的，这些就都可以忽略不去计算。

运用Apriori算法的思想，我们就能去掉很多非频繁的项集，大大简化计算量。

2.3 Apriori算法流程

要使用Apriori算法，我们需要提供两个参数，数据集和最小支持度。我们从前面已经知道了Apriori会遍历所有的物品组合，怎么遍历呢？答案就是递归。先遍历1个物品组合的情况，剔除掉支持度低于最小支持度的数据项，然后用剩下的物品进行组合。遍历2个物品组合的情况，再剔除不满足条件的组合。不断递归下去，直到不再有物品可以组合。

2.4 Apriori算法实现

（1）数据集处理

采用Groceries数据集，我们需要的数据格式是：List of List，每一个购物清单是一个list，所有的购物清单也构成一个List。

    with open(filename)as f:
    f_csv = csv.reader(f)
    for index, val in enumerate(f_csv):
        if index != 0:
            goodsList = str(val[1]).replace('}','').replace('{','').split(',')
            # print(str(type(goodsList)))
            data_set.append(list(goodsList))

（2）项的排列组合
create_Ck

Ck = set()
len_Lksub1 = len(Lksub1)
list_Lksub1 = list(Lksub1)
for i in range(len_Lksub1):
    for j in range(1, len_Lksub1):
        l1 = list(list_Lksub1[i])
        l2 = list(list_Lksub1[j])
        l1.sort()
        l2.sort()
        if l1[0:k - 2] == l2[0:k - 2]:
            Ck_item = list_Lksub1[i] | list_Lksub1[j]
            # pruning
            if is_apriori(Ck_item, Lksub1):
                Ck.add(Ck_item)
return Ck

is_apriori

    for item in Ck_item:
    sub_Ck = Ck_item - frozenset([item])
    if sub_Ck not in Lksub1:
        return False
return True

（3）频繁项集的计算
将获得的所有排列组合，计算支持度。

generate_Lk_by_Ck

support_data = {}
C1 = create_C1(data_set)    # 获得一层候选项集
L1 = generate_Lk_by_Ck(data_set, C1, min_support, support_data) # 获得一层频繁项集
print("len-lk:" + str(len(list(L1))) + "  L1:" + str(L1))
Lksub1 = L1.copy()
L = []
L.append(Lksub1) # List of List
for i in range(2, k + 1): # 多层频繁项集的获取
    Ci = create_Ck(Lksub1, i)
    Li = generate_Lk_by_Ck(data_set, Ci, min_support, support_data)
    Lksub1 = Li.copy()
    L.append(Lksub1)
return L, support_data # L是所有的频繁项集，按照层数保存的List of List，support_data是频繁项集和支持度的键值对

generate_Lk_by_Ck

Lk = []
item_count = {}
for t in data_set: # 遍历所有条目
    for item in Ck: # 候选k阶频繁项集循环
        if item.issubset(t): # item是否是t的子集 ，并计数存到item_count
            if item not in item_count:
                item_count[item] = 1
            else:
                item_count[item] += 1
t_num = float(len(data_set))
for item in item_count:
    if (item_count[item] / t_num) >= min_support: # 支持度比较
        print('LK add : ' + str(item))
        Lk.append(item)
        support_data[item] = item_count[item] / t_num
print('LK:' + str(Lk))
return Lk # 返回频繁项集

（4）置信度的计算
传入最小置信度，然后将所有的置信度进行计算，大于最小置信度的条件概率，计入新的list。
generate_big_rules

big_rule_list = []
sub_set_list = []
for i in range(0, len(L)): # 遍历频繁项集
    for freq_set in L[i]: # 频繁项集
        for sub_set in sub_set_list:
            if sub_set.issubset(freq_set):
                # print("sub_set:" + str(sub_set))
                # print("freq_set:" + str(freq_set))
                conf = support_data[freq_set] / support_data[freq_set - sub_set] # 支持度计算
                big_rule = (freq_set - sub_set, sub_set, conf)
                # print("freq_set - sub_set:" + str(freq_set - sub_set))
                if conf >= min_conf and big_rule not in big_rule_list:
                    # print freq_set-sub_set, " => ", sub_set, "conf: ", conf
                    big_rule_list.append(big_rule)
            # print("+++++++")
        sub_set_list.append(freq_set)
return big_rule_list

源码

下面我们来用Apriori算法实战一下吧。

三. Apriori算法实战

我们用一个简单的例子来用一下Apriori吧，这里用到的库是mlxtend。

在放代码之前，先介绍下Apriori算法的参数吧。

def apriori(df, min_support=0.5, use_colnames=False, max_len=None)

参数如下： df：这个不用说，就是我们的数据集。 min_support：给定的最小支持度。
use_colnames：默认False，则返回的物品组合用编号显示，为True的话直接显示物品名称。
max_len：最大物品组合数，默认是None，不做限制。如果只需要计算两个物品组合的话，便将这个值设置为2。

OK，接下来就来用一个简单的例子来看看怎么使用Apriori算法找到频繁项集吧。

import pandas as pd 
from mlxtend.preprocessing import TransactionEncoder 
from mlxtend.frequent_patterns import apriori #设置数据集 

dataset = [
    ['牛奶','洋葱','肉豆蔻','芸豆','鸡蛋','酸奶'], 
    ['莳萝','洋葱','肉豆蔻','芸豆','鸡蛋','酸奶'], 
    ['牛奶','苹果','芸豆','鸡蛋'], 
    ['牛奶','独角兽','玉米','芸豆','酸奶'], 
    ['玉米','洋葱','洋葱','芸豆','冰淇淋','鸡蛋']
] 
te = TransactionEncoder() #进行 one-hot 编码 
te_ary = te.fit(records).transform(records) 
df = pd.DataFrame(te_ary, columns=te.columns_) #利用 Apriori 找出频繁项集 
freq = apriori(df, min_support=0.05, use_colnames=True)

首先，需要先将商品进行one-hot编码，编码后用boolean值表示。所谓ont-hot编码呢，直观来说就是有多少个状态就有多少比特，而且只有一个比特为1，其他全为0的一种码制。比如冰淇淋只存在最后一共交易单中，其他交易中都没出现。那冰淇淋就可以用[0,0,0,0,1]来表示

这里编码后的数据如下：

冰淇淋 洋葱 牛奶 独角兽 玉米 肉豆蔻 芸豆 苹果 莳萝 酸奶 鸡蛋
0 False True True False False True True False False True True
1 False True False False False True True False True True True
2 False False True False False False True True False False True
3 False False True True True False True False False True False
4 True True False False True False True False False False True
我们设定的最小支持度是0.6，那么只有支持度大于0.6的物品集合才是频繁项集，最终结果如下：

support itemsets 0 0.6 (洋葱) 1 0.6 (牛奶) 2 1.0 (芸豆) 3 0.6 (酸奶) 4 0.8 (鸡蛋) 5 0.6 (芸豆, 洋葱) 6 0.6 (洋葱, 鸡蛋) 7 0.6 (牛奶, 芸豆) 8 0.6 (酸奶, 芸豆) 9 0.8 (芸豆, 鸡蛋) 10 0.6 (芸豆, 洋葱, 鸡蛋)
四. 小结
今天我们介绍了关联分析中会用到的几个概念，支持度，置信度，提升度。然后讲述了Apriori算法的作用，以及Apriori算法如何高效得找出物品的频繁项集。

最后使用Apriori算法找出例子中的频繁项集。