第七章 查找
一、基本概念
-
查找表: 由同一类型的数据元素(或记录)构成的集合
| 静态查找表 | 查找的同时对查找表不做修改操作(如插入和删除等) |
| 动态查找表 | 查找的同时对查找表具有修改操作 |
- 关键字:记录中某个数据项的值,可用来识别一个记录
- ASL(关 键 字 的 平 均 比 较 次 数 或 平 均 搜 索 长 度):为确定记录在查找表中的位置,需和给定值进行比较的关键字个数的期望值 【ASL = (c1p1 + c2p2 + ... + cnpn) / n 其中pi是查找第i条记录的概率,ci为查找第i条记录需要比较的次数】
二、学习框架(如图)

三、知识点
(一)线性表的查找(静态)
1. 顺序查找(不要求表中元素有序)
(1)查找算法

/* 普通做法 //n个数,循环n次,每次比较两次,T(n)=2*n int Search_Seq(SSTable ST, KeyType key) {//若成功返回其位置下标i,否则返回-1 for(i=1;i<=ST.length;i++) { if(key==ST.R[i].key) return i; } return -1; }*/ //可免去查找过程中每一步都要检测是否查找完毕,加快速度,T(n)=n; int Search_Seq(SSTable ST, KeyType key) {//若成功返回其位置下标i,否则返回0 ST.R[0].key = key; //把待查关键字key存入表头(做哨兵)—>不会越界访问 for(i=ST.length; ST.R[i].key!=key; --i ); //从后向前逐个比较 return i; //找不到的key返回下标为0 }
(2)性能分析:(1)ASL(查找成功,且假设查找概率相等)= (1+2+......+n)/n = (n+1)/2; (2)ASL (查找不成功)= (n+1)*1;
2. 折半查找(有序)——【每次查找范围缩小一半,直到找到/找不到】
(1)分析:mid = ( low+high)/2;(假设在表a中)
a[mid] == key ->找到;
a[mid] < key —>key在mid右段,high不变,low = mid+1;
a[mid] > key —>key在mid左段,low不变,high = mid-1;【注意:如果进入循环条件为while(low <=high)不可以写成high = mid—>会导致查找的key大于表中所有数时陷入死循环】
(2)查找算法

//非递归算法 int Search(SSTable ST, KeyType key) { int low = 1, high = ST.length;//初始化 while(low <= high) { mid = (low+high) / 2; if(key == ST.R[mid].key) return mid;//找到则函返回在表中的位置下标 else if(key < ST.R[mid].key) high = mid-1; //左段查找 else low = mid + 1; //右段查找 } return 0; //表中不存在待查元素,返回0 }

//递归算法 int Search(SSTable ST, KeyType key, int low, int high) { if(low >high) return 0;//找不到则return 0; mid = (low+high) / 2; if(key == ST.R[mid].key) return mid;//找到则return所在表中的下标 else if(key < ST.R[mid].key) return Search(ST,key,low,mid-1);//递归查找左段 else return Search(ST,key,mid+1,high);//递归查找右段 }
【注意:找不到情况下 —>(1)low>high, 且low=high+1; (2)a[high]<key<a[low] ; (3) 大于key的最小值为啊[low], 小于key的最大值为a[high] 】
(3)性能分析:每次将待查记录所在区间缩小一半,比顺序查找效率高,时间复杂度O(log2n)。
3.分块查找(块间有序,块内无序)
(1)索引表:存放各子表中的最大关键字以及每个分块子表的起始地址;表及其索引表结构大致如图所示(这种查找方法没有细讲算法就跳过了)
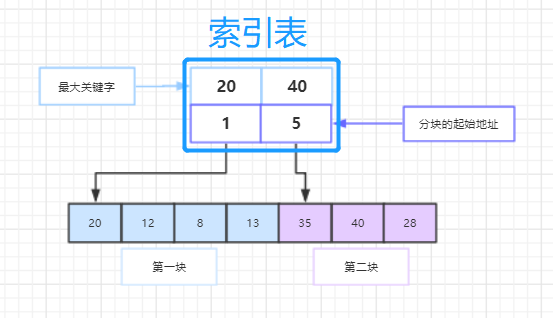
(2)性能分析:ASL = Lb(对索引表查找的ASL) + Lw(对块内查找的ASL)= 1/2(n/s+s)+1 //n为表长,s为每分块含的记录数
(二)树表的查找(动态)
1. 二叉排序树
(1)什么是二叉排序树——二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:①若它的左子树不空,则左子树上所有结点的值均小千它的根结点的值;②若它的右子树不空,则右子树上所有结点的值均大千它的根结点的值;③它的左、 右子树也分别为二叉排序树。
(2)数据结构——一般取二叉链表作为二叉排序树的存储结构

typedef struct { // 结点的数据域结构 KeyType key; //关键字项 InfoType otherinfo; // 与关键字相关的其他数据项 } ElemType; typedef struct BSTNode { // 结点结构 ElemType data; struct BSTNode *lchild, *rchild; // 左右孩子指针 } BSTNode, *BSTree;
(3)算法

void InsertBST(BSTree &T, ElemType e ) { // 当二叉排序树T中不存在关键字等于e.key的数据元素时插入该元素。 if (T == NULL) {//树为空则作为根结点 s = new BSTNode; s->data = e; s->lchild = s->rchild = NULL; T = s; } else if (e.key < T.data.key) //小于根结点值,递归插入左子树 InsertBST(T -> lchild, e); else if (e.key > T.data.key) //大于根结点值,递归插入右子树 InsertBST(T -> rchild, e); }

BSTree SearchBST(BSTree T, KeyType key) {//二叉排序树查找 if((T==NULL) || key==T->data.key) return T; else if(key < T->data.key) //在左子树中继续查找 return SearchBST(T->lchild, key); else //在右子树中继续查找 return SearchBST(T->rchild, key); }

//二叉树的生成本质上建立在查找插入上 void CreatBST(BSTree &T) {//依次读入结点信息,将此结点插入到二叉排序树T中 T = NULL; //初始化 input(e); //e为ElemType类型,包括key、otherinfo while(e.key != ENDFLAG) { //ENDFLAG根据题目而定,可能为-1等 InsertBST(T,e); input(e) ; } }
(4)性能分析:最好——ASL(二叉树形态匀称)= log2n;最坏——ASL(二叉树为单支树)= (n+1)/2
2. 平衡二叉树
(1)部分概念
- 平衡二叉树又称AVL树(特殊的二叉排序树):① 左、右子树是平衡二叉树;②所有结点的左、右子树深度之差的绝对值≤1
- 平衡因子: 该结点左子树与右子树的高度差
- 平衡旋转:插入新结点时重新调整树的结构,使之恢复平衡的调整过程
- 最小不平衡子树:离插入结点最近且平衡因子绝对值超过1的祖先结点
(2)如何调整树——①调整目标:最小不平衡子树;②调整原则:保持有序+平衡 ;③分情况调整:LL, RR, LR, RL
3. 多路查找树
(1)多路查找树一次能得到最多M-1(M:树的阶)个键值的信息——适用于要求查找深度小的检索
(2)应用:在大规模数据存储的索引查询中,由于无法一次性加载所有索引数据到内存里,所以在索引查询时要进行内外存交换。而内外存交换次数越少,效率表现也越高
(3)B树是一种平衡的多路查找树;在B树中进行查找时,其查找时间主要花费在搜索结点(访问外存)上,即 主要取决于B树的深度
(4)B+树是B树的一种变形。(通过链表将叶子节点串联在一起,这样可以方便按区间查找)
(三)散列表的查找
1. 部分概念
- 散列函数(hash函数):散列方法中使用的转换函数
- 散列表(hash表):存储按散列函数计算得到相应散列地址的数据记录的有限连续地址空间(一般为一维数组)
- 冲突:不同的关键码映射到同一个散列地址。即key1!=key2,但H(key1)==H(key2)
- 同义词:具有相同函数值的两个关键字。
- 散列表的装填因子α = 表中填入的记录数/哈希表的长度【α越大,表中记录数越多,说明表装得越满,发生冲突的可能性就越大,查找时比较次数就越多】
2. 散列函数的构造方法
(1)数字分析法:从关键字中提取分布均匀的若干位或他们的组合作为地址
(2)平方取中法:取关键字平方后的中间几位或其组合作为散列地址,则使随机分布的关键字得到的散列地址也是随机的
(3)折叠法:将关键字分割成位数相同的几部分(最后一部分的位数可以不同),然后取这几部分的叠加和(舍去进位) 作为散列地址
(4)除留余数法:假设散列表表长为m, 选择一个不大千m的数p, 用p去除关键字,除后所得余数为散列地址,即H(key) = key%p (p为小于表长的最大质数)
3.处理冲突的方法
(1)思想:把具有相同散列地址的记录放在同一个单链表中,称为同义词链表。有 m 个散列地址就有 m 个单链表,同时用数组 HT[O…m-1]存放各个链表的头指针,凡是散列地址为 i的记录都以结点方式插入到以 HT[i]为头结点的单链表中。
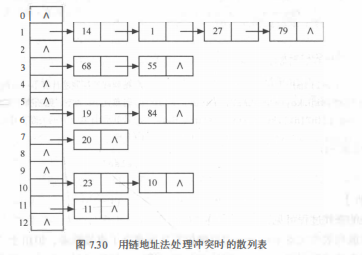
(4)哈希表的查找

#define NULLKEY 0 //散列表为空标记 int SearchHash(HashTable HT,KeyType key) { HO=H (key); //根据散列函数H (key)计算散列地址 if(HT[HO].key==NULLKEY) return -1; //查找不成功,返回-1 else if(HT[HO].key==key) return HO; // 查找成功,返回所在下标 else {//线性探测法处理冲突 for(i=1;i<m;++i) { Hi=(HO+i); if(HT[Hi] .key==NULLKEY) return -1; else if(HT[Hi] .key==key) return Hi; } return -1; } }
(5)性能分析

四、比较
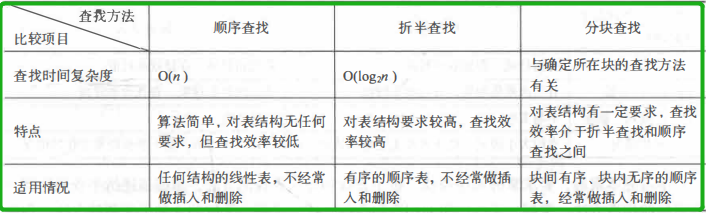
1.顺序查找、折半查找和分块查找的比较
2.折半查找和二叉排序树查找的比较

3.多路查找树
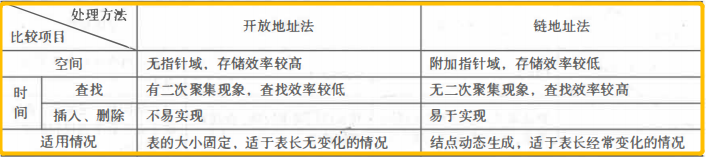
4.开放地址法和链地址法的比较
五、作业
1.实践1 —— 二分查找变形,设a[0:n-1]是按非降序排列的数组,请改写二分查找算法,查找自左向右第一个大于等于x的值。若不存在这样的数,输出-1
- 我的做法比较简单粗暴,按二分查找的算法,找到的时候再来个顺序查找第一个小于key的值a,再通过a的下标+1,得到第一个自左向右第一个大于等于x的值

int Search(SSTable S, int Key) {//二分查找表S中是否存在Key int low = 0, high = S.length-1; int mid, i; while(low<=high) { mid = (low+high)/2; if(S.R[mid].key == Key) {//存在Key //for(i=mid;S.R[i].key==Key;i--);//这种情况i下标可能小于0,而导致越界访问 for(i=mid;S.R[i].key==Key&&i>-1;i--);//查找值为Key的最小下标,即自左向右第一个等于x的值的下标 return i+1;//循环中退出时i为S.R[i].key!=Key,所以i+1才是为Key的最小下标 } else if(S.R[mid].key < Key) low = mid+1; else high = mid -1; } //循环退出的情况都是low>high,如果low大于等于表长,则不存在等于x的值的下标, if(low>=S.length) return -1; else return low; }
【这个过程我还有个错误,查找的数据是小于所有数据的时候,是返回第一个数据,而不是不存在大于他数返回-1】
- 但是有更好的做法——S.R[mid].key==Key时我们继续向左段缩小查找范围,直到low>high,而此时的low,就是第一个大于n的数据,也就是左向右第一个等于Key的下标这种写法代码就更简单,时间复杂度也比第一种小

/*我的理解:(可能有更简洁的理解) 在S.R[mid].key < Key的情况,我们向右段缩小查找范围 而S.R[mid].key > Key的情况,我们向左段缩小查找范围 在S.R[mid].key == Key的情况下,表S中的数据是按照按非降序排列 所以二分查找S.R[mid].key==Key时,可能下标不是自左向右第一个等于x的值的下标 【假设我们查的数 n = 介于第一个小于Key与Key之间 的数据 (其实就是类似查找那个小于数据中最大值的数时返回第一个大于他的数同个道理】 那么S.R[mid].key==Key时我们继续向左段缩小查找范围,直到low>high,而此时的low,就是第一个大于n的数据,也就是左向右第一个等于Key的下标 这种写法代码就更简单,时间复杂度也比法一小 */ int Search(SSTable S, int Key) {//二分查找表S中是否存在Key int low = 0, high = S.length-1; int mid, i; while(low<=high) { mid = (low+high)/2; if(S.R[mid].key < Key) low = mid+1; else high = mid -1; } //循环退出的情况都是low>high,如果low大于等于表长,则不存在等于x的值的下标, if(low>=S.length) return -1; else return low; }
2.作业 —— Hashing(英文题目,打扰了)
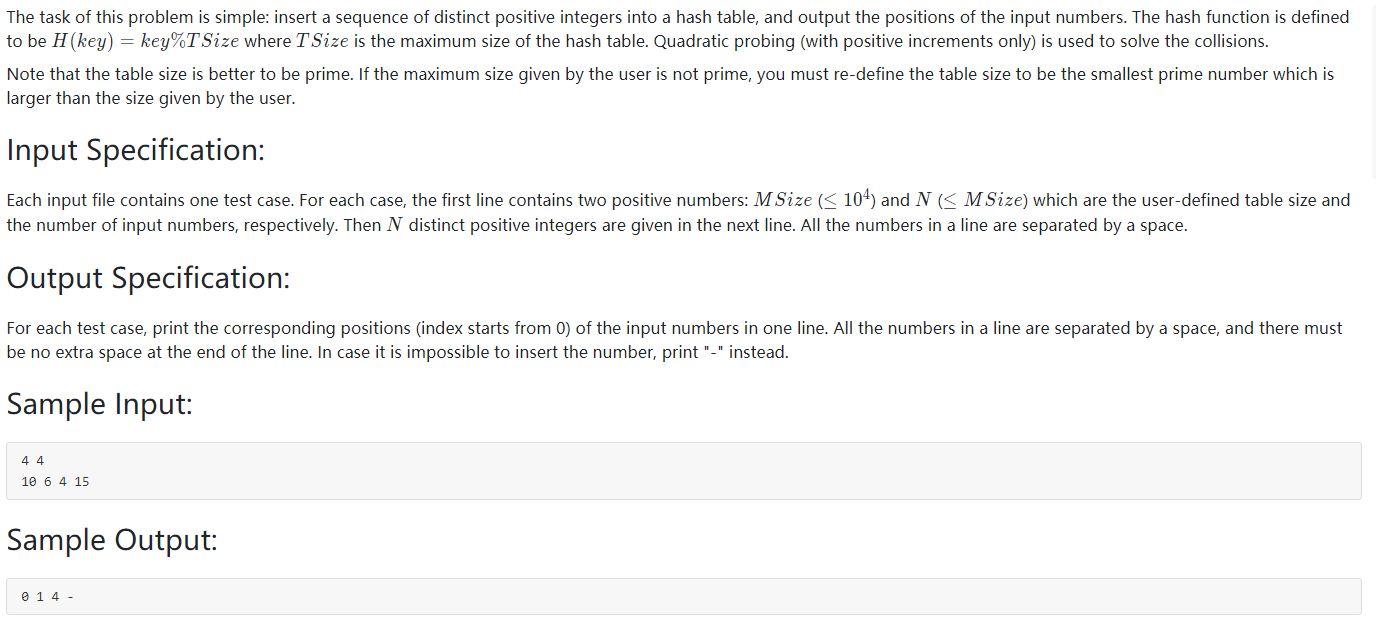
注意:(1)用平方探测处理冲突,且只取正的,即di = 12,22,32,… +k2 (k<=m/2);(2)读入表长不为素数则要找大于他的最小素数;(3)H(key)=key%TSize;
我一开始的代码感觉好冗余,打包的函数太多的样子,而且变量太多还懵叉叉的冲突的时候有处理查找新的下标,但输出却输出成原来的H(key),不过基本思路没有问题。哦还有就是忘了释放数组空间了。

#include<iostream> #include<math.h> using namespace std; typedef struct{ int *H; int length; }Hash; bool isPrime(int len) {//检查len是否为素数 if (len==1) return 0 ; int t; for(int i=2; i<=sqrt(len); i++) { t= len % i ; if(t == 0) return 0; } return 1; } int largerPrime(int len) {//查找大于len的最小质数 int i; for(i=len+1; !isPrime(i); i++); return i; } /*void creat(Hash &h) {//创建空哈希表,并初始化为0 int len; cin >> len; if(isPrime(len)) //len为质数 h.length = len; else //len不为质数,查找大于len的最小质数作为哈希表长 h.length = largerPrime(len); h.H = new int[h.length](); //这样没法释放空间的样子,所以放到主函数去了 }*/ void insert(Hash &h) { int n, num,hashkey; cin >>n; for(int t=0;t<n;t++) { cin >>num; hashkey = num%h.length; if(h.H[hashkey]==0) {//未写入数据 h.H[hashkey] = num; if(t==0) cout << hashkey; else cout <<" " << hashkey; } else //已写入数据 { int d=0;//间隔 int flag = 0; for (int k = 0; k <=h.length/2; k++ ) //k<h.length也不行 {//平方探测(+) d = 1,4,9… d = k*k; int newhashkey = (hashkey+d)%h.length; if(h.H[newhashkey]==0) { h.H[newhashkey] = num; if(t==0) cout << newhashkey;//好粗心,这里写错成hashkey,所有最后一个点老出错 else cout <<" " << newhashkey; flag = 1; break; } } if(flag == 0) {//没法插入的情况 if(t==0) cout << "-"; else cout <<" -"; flag = 1; } } } } int main() { Hash h; //创建空哈希表,并初始化为0 int len; cin >> len; if(isPrime(len)) //len为质数 h.length = len; else //len不为质数,查找大于len的最小质数作为哈希表长 h.length = largerPrime(len); h.H = new int[h.length](); insert(h); delete[]h.H; return 0; }
但是这样应该会更简洁一些

#include<iostream> #include<math.h> using namespace std; typedef struct{ int *H; int length; }Hash; bool isPrime(int len) {//检查len是否为素数 if (len==1) return 0 ; int t; for(int i=2; i<=sqrt(len); i++) { t = len % i ; if(t == 0) return 0; } return 1; } void insert(Hash &h) { int n, num; cin >>n; for(int t=0;t<n;t++) { cin >>num; int flag = 0; for (int k = 0; k<h.length; k++ ) {//平方探测(+) d = 1,4,9… int newhashkey = (num+k*k)%h.length; if(h.H[newhashkey]==0) { h.H[newhashkey] = num; if(t==0) cout << newhashkey; else cout <<" " << newhashkey; flag = 1; break; } } if(flag == 0) {//没法插入的情况 if(t==0) cout <<"-"; else cout <<" " << "-"; flag = 1; } } } int main() { Hash h; int len; cin>>len; while(!isPrime(len)) len++; h.length=len; h.H=new int [h.length]();//初始化为0 insert(h); delete []h.H; return 0; } hashing-2.0
来着xn同学更简洁的代码

#include<iostream> using namespace std; bool jugde(int m) {//判断是否为素数 if(m==1) return false; if(m==2||m==3) return true; for(int i=2;i<m;i++) { if(m%i==0) return false; } return true; } int main() { int m,n,x; cin>>m>>n; while(!jugde(m))//表长为素数的处理 m++; int flag=0; int b[10000]={0}; for(int i=0;i<n;i++) { cin>>x; int j=0;//间隔 while(j<m) { int k=x+j*j;//二次平方处理 if(b[k%m]==0) { if(flag==0) cout<<k%m; else cout<<" "<<k%m; flag++; b[k%m]=x; break; } j++; } if(j==m) {//无法插入 if(flag==0) cout<<"-"; else cout<<" -"; flag++; } } return 0; }
