前言
支持向量机是最重要的机器学习算法之一，支持向量机的一个重要特点是通过核函数进行非线性分类。本文深度剖析了核函数的含义，并从该角度去理解线性回归和非线性分类的问题。
目录
1、线性回归的核函数表示
2、核函数含义解析
3、核函数含义理解线性回归
4、核函数含义理解非线性分类
5、核函数的应用范围
6、总结
1、线性回归的核函数表示
我们先通过构建最优线性回归模型来引出核函数的表达式。
总结：
（1）1.5式就是传说中的核函数方程，核函数方程的展开式有很多种情况，这一节的核函数方程展开式是基函数向量的内积。
（2）1.4式是线性回归的核函数对偶形式，对偶形式都会包含下面这项：
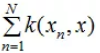
2、核函数含义解析
我们用1.5式和1.6式来解析核函数的含义。
1.5式和1.6式结合，得：
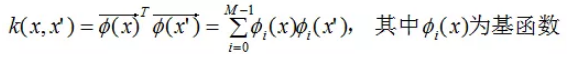
上式表示，先对输入变量映射为特征空间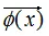
，然后在该特征空间下内积。
现在，我们考虑三种常用的基函数，分别为多项式基函数，高斯基函数，S型基函数。
令输入变量x'为常数，x'的值用红色叉号表示，可以画出x与k(x,x')的关系曲线：
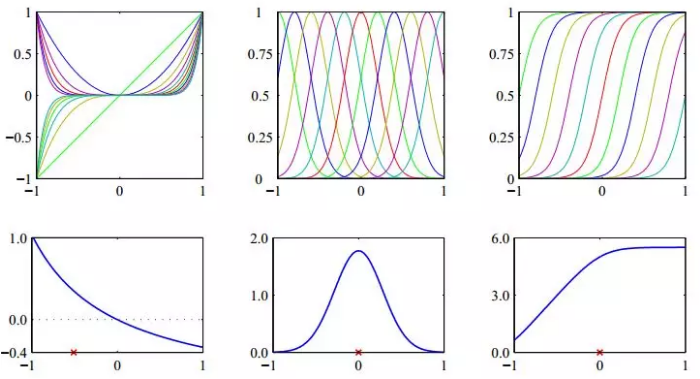
图的第一行为基函数曲线，第二行为x与核函数k(x,x')的曲线。
由上图可知，核函数k(x,x')取得最大值的必要条件是x=x'，核函数值的大小可以表示两个输入变量x和x'的相似度。举例说明这一含义：
如上图第二列，归一化的正态分布在x=0具有最大概率，当两个输入变量值都是0时，核函数具有最大值，它们的相似度最高。
如上图第三列，S型函数值表示P(y=1|x)的概率，当两个输入变量都是1时，核函数具有最大值，它们的相似度最高。
因此，核函数的含义可以用相似度来解释，若两个输入变量的特征空间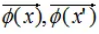
都较大，则两个输入变量在该核函数下具有较高的相似度。
3、核函数含义理解线性回归
为了阅读方便，1.4式预测目标表达式：
结论
线性回归可以理解成训练目标值的权值相加，权值与核函数成正比，若输入特征与某一训练样本的特征相似度越高，相应的核函数越大，则对应的权值就越大，该训练样本的目标变量对预测目标变量的影响亦越大。
4、核函数含义理解非线性分类
解决如下图的二分类问题，不同形状表示不同的类。
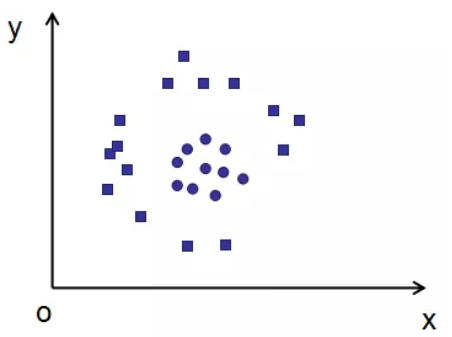
（1）显示映射法
分类效果图如下：
（2）核函数法
我们知道核函数的含义是相似度，我们考虑用高斯核函数进行分类，高斯核函数用样本的相对距离来表示相似度，若相对距离越小，则相似度越大，反之相似度越小。
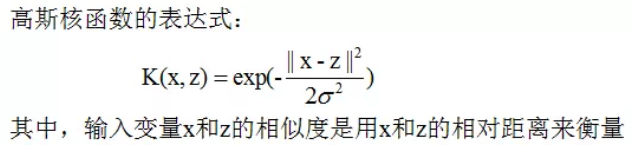
首先用核函数将低维映射成高维空间，然后用线性支持向量机的方法进行分类（后续文章会详细讲支持向量机算法）。
请用核函数法
第二节用显示映射函数的方法说明了核函数的含义，这一节用该方法求决策函数，但是这种方法难点在于定义显示映射函数，而核函数法是隐式的映射特征空间且核函数法计算k(x,x')比较容易，因此推荐核函数法作特征的多维映射。
核函数的应用范围
这一节用一句话来概括：凡是有特征内积出现的式子都可以用核函数来代替。
如下图：
左边为核函数，右边为内积。
总结
本文详细的解释了核函数的含义——相似度，然后从核函数的角度去理解线性回归和非线性分类，核函数是隐式的特征空间映射，不需要定义特征映射函数。特征内积出现的式子都可以用核函数来代替，因此，核函数在支持向量机的非线性分类具有不可替代的作用。
参考
李航 《统计学习方法》
Christopher M.Bishop <<Pattern Reconition and Machine Learning>>
