Adaptive Sampled Softmax with Kernel Based Sampling

目录

• 概
• 符号说明
• Motivation
• 本文的方法
• Kernel 的选择

Blanc G. and Rendle S. Adaptive sampled softmax with kernel based sampling. In International Conference on Machine Learning (ICML), 2018.

概

这儿 已经讨论了现在的概率估计 (主要是负样本采样的方式) 是存在 bias 的, 这篇文章用 kernel 的方法来建模和解决这个问题.

符号说明

• \(\bm{x} \in \mathcal{X}\), 样本;
• \(\bm{o}: \mathcal{X} \times \Theta \rightarrow \mathbb{R}^n\), 将输入映射为一个 \(n\) 维 (\(n\) 表示总的类别的数目, 这个类别或许需要打引号, 比如在语言模型中每一个词就是一个类, 在推荐系统中, 每个 item 就可以看作是一个类);
• \(\bm{y} \in [0, 1]^n, \sum_i y_i = 1\), 每个类对应概率;
• \(\bm{s} \in \{1, \ldots, n\}^{m+1}\), \(\bm{s}\) 是用于训练的样本, 包括一个正样本加上 \(m\) 个采样的负样本, 需要注意的是 \(\bm{s}\) 中的元素是可以重复的, 比如 \(\bm{s} = (2, 6, 7, 6, 3)\), 正样本为 \(2\), 而负样本 \(6\) 出现了两次;

Motivation

• 我们通常会建模这样的概率分布:

  \[p_i := \frac{\exp(o_i)}{\sum_{j=1}^n \exp(o_j)}, \]

  并通过如下的损失来优化:

  \[\tag{1} L(\bm{y}, \bm{p}) = -\sum_{i=1}^n y_i \log p_i = \log \sum_{i=1}^n \exp(o_i) - \sum_{i=1}^n y_i o_i; \]

• 但是, 因为 (1) 需要计算所有的 \(n\) 个 \(\exp(o_j(\bm{x}))\), 而且这个值往往是由 \(\bm{x}\) 和 \(j\) 共同决定的, 所以很费时, 此时我们需要用 这儿 的校正的结果:

  \[o_i' = o_i - \log (q_i), \]

  并有

  \[\tag{2} p_i' := \frac{\exp(o_i')}{\sum_{j=1}^{m+1} \exp(o_j')}; \]

  注意: 此时 \(j\) 必须采样于 \(q\);

• \(q_i\) 越接近真实的 \(p_i\), (2) 所存在的 bias 就越小;

• 但是我们注意到, 这个问题, 即建模 \(q\) 的问题有以下几个问题:

  1. \(q_i\) 实际上是 \(q_i(\bm{x})\), 不同的样本 \(\bm{x}\) 分布是不同的;
  2. 随着模型的训练, \(q_i\) 也是会发生变化的.

本文的方法

• 首先作者假设 \(o_j(\bm{x})\) 是通过 \(\bm{x}\) 的 embedding \(\bm{h} \in \mathbb{R}^d\) 和类别的 embedding \(\bm{w}_j \in \mathbb{R}^d\) 通过内积得到的:

  \[o_j(\bm{x}) = \langle \bm{h}, \bm{w}_j \rangle; \]

• 然后通过如下方式建模 \(q_i\):

  \[q_i = \frac{K(\bm{h}, \bm{w}_i)}{\sum_{j=1}^n K(\bm{h}, \bm{w}_j)} = \frac{K(\bm{h}, \bm{w}_i)}{\langle \phi(\bm{h}), \underbrace{\sum_{j=1}^n \phi(\bm{w}_j)}_{=:\bm{z} \in \mathbb{R}^D} \rangle}, \]

  倘若我们能够提前计算出 \(\bm{z}\), 那么 \(q_i\) 的建模就只和 \(\bm{h}, \bm{w}, \bm{z}\) 有关了;

• 当 \(n\) 很大的时候, 想要从 \(q\) 中采样依旧是一个非常耗时的事情, 但是基于 kernel 的方法有它的特别之处, 如下图所示:

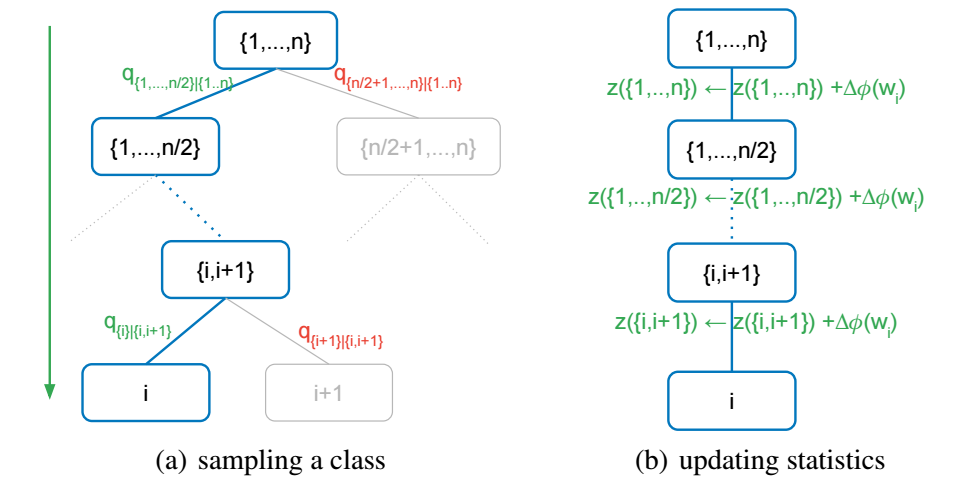
1. 首先将 \(C = \{1, \ldots, n\}\) 均分成两组, 记作 \(C_1, C_2\), 然后我们首先根据

   \[\begin{array}{ll} q_{C'|C} &= \sum_{j \in C'} \frac{K(\bm{h}, \bm{w}_j)}{\sum_{l \in C} K(\bm{h}, \bm{w}_l)} \\ &= \frac{\sum_{j \in C'} K(\bm{h}, \bm{w}_j)}{\sum_{l \in C} K(\bm{h}, \bm{w}_l)} \\ &= \frac{\langle \phi(\bm{h}, \bm{z}(C'))}{\langle \phi(\bm{h}, \bm{z}(C))}, \quad C' \in \{C_1, C_2\} \end{array} \]

   来采样 \(C_1, C_2\), 注意, 此时我们需要维护两个额外的向量

   \[\bm{z}(C_1) = \sum_{j \in C_1} \phi(\bm{w}_j) \\ \bm{z}(C_2) = \sum_{j \in C_2} \phi(\bm{w}_j); \\ \]

2. 在选到 \(C'\) 上重复 1 的操作直到 \(|C'| = 1\);

3. 在每次更新完参数之后, 记得更新 \(\bm{z}(C')\).

此时可以发现, 总的采样次数降为 \(\mathcal{O}(\log_2 n)\), 特别地,

\[\begin{array}{ll} & q_{C_1|C} q_{C_2|C_1} \ldots q_{i|C_{\log n -1}}\\ =& \frac{\langle \phi(\bm{h}), \bm{z}(C_1) \rangle}{\langle \phi(\bm{h}), \bm{z}(C) \rangle} \frac{\langle \phi(\bm{h}), \bm{z}(C_2) \rangle}{\langle \phi(\bm{h}), \bm{z}(C_1) \rangle} \cdots \frac{\langle \phi(\bm{h}), \phi(\bm{w}_i) \rangle}{\langle \phi(\bm{h}), \bm{z}(C_{\log n -1}) \rangle} \\ =&\frac{\langle \phi(\bm{h}), \phi(\bm{w}_i) \rangle}{\langle \phi(\bm{h}), \bm{z}(C) \rangle} = q_i, \end{array} \]

是和原来的是一样的, 只是我们需要多维护几个向量.

Kernel 的选择

作者选择了 \(K(\bm{h}, \bm{w_i}) = \alpha \langle \bm{h}, \bm{w}\rangle^2 + 1\), 此时

\[\phi(\bm{z}) = [\sqrt{a}\text{ vec}(\bm{a} \otimes \bm{a}), 1], \]

因为在原点附近它对 \(\exp\) 是一个很好的估计, 此外, 因为二次多项式核对于负 logits 的拟合不是很好, 作者同时将原先的概率建模为:

\[p_i := \frac{\exp(|o_i|)}{\sum_{j=1}^n \exp(|o_j|)}, \]

以保证所有的 score 都是正的. 二者便兼容了.

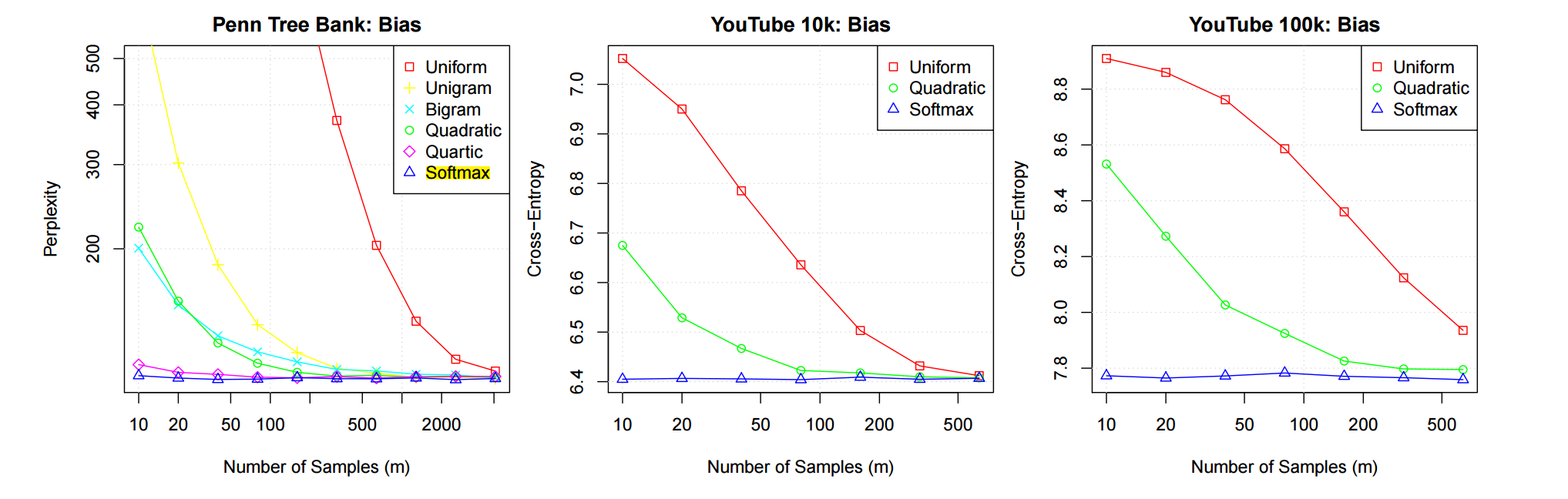
上图是一个测试结果, 其中 Softmax 表示采用最佳的逼近, 即

\[q_i = p_i. \]