概
本文提出了一种基于图的 Mask AutoEncoder 方法, 主要创新点是 mask 和 cosine error 的使用.
符号说明
- \(\mathcal{G} = (\mathcal{V}, A, X)\), 图;
- \(|\mathcal{V}| = N\), 结点;
- \(A \in \{0, 1\}^{N \times N}\), 邻接矩阵;
- \(X \in \mathbb{R}^{N \times d}\), 输入的特征矩阵;
- \(H = f_E(A, X)\), encoder 将 \(A, X\) 映射为隐变量 \(H\);
- \(\mathcal{G}' = f_D(A, H)\), decoder 将隐变量 \(H\) 映射为 \(\mathcal{G}'\).
本文方法
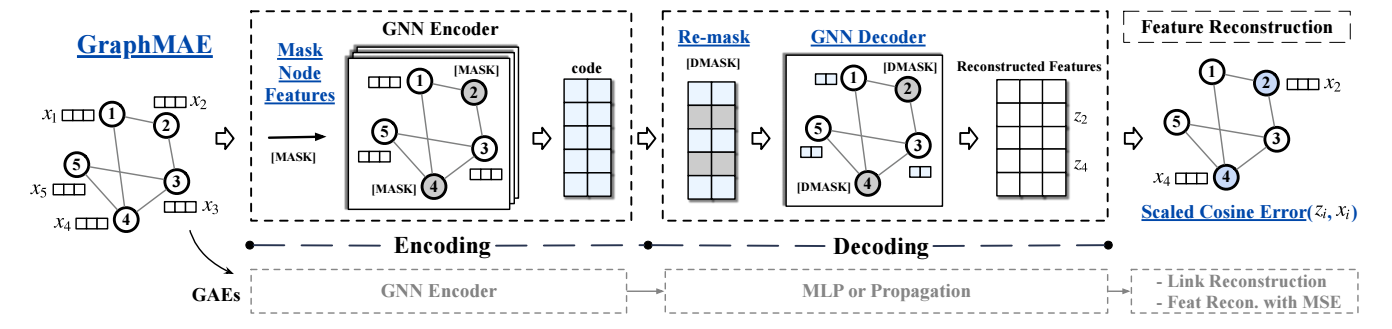
-
以往的基于图的 AutoEncoder 方法, 大抵是预测 edge, 实际上就是重构邻接矩阵 \(A\), 但是实际上图中最重要的还是结点的特征 \(X\) [58], 所以本文着重于特征的重构;
-
首先, 给定特征 \(X\), 我们均匀随机采样一个子集 \(\tilde{\mathcal{V}} \subset \mathcal{V}\), 并定义输入:
\[\tilde{x}_i = \left \{ \begin{array}{ll} x_{[M]} & v_i \in \tilde{\mathcal{V}} \\ x_i & v_i \not \in \tilde{\mathcal{V}} \\ \end{array} \right . \]其中 \(x_{[M]}\) 是一个 Mask token 对应的特征;
-
经过 GNN Encoder (这里作者推荐用 GAT [39] 或者 GIN [45], 表达能力强一些) 进行特征提取后得到:
\[H = f_E(A, X); \] -
对 \(H\) 进行 re-mask:
\[\tilde{h}_i = \left \{ \begin{array}{ll} h_{[M]} & v_i \in \tilde{\mathcal{V}} \\ h_i & v_i \not \in \tilde{\mathcal{V}} \\ \end{array} \right . \] -
通过 Decoder 重构
\[Z = f_D(A, \tilde{H}), \]这里作者推荐用单层的 GNN 而不是诸如 MLP 等缺乏表达能力 (没有结合周围点的能力) 的结构;
-
训练的时候采用如下的 scaled cosine error (SCE):
\[\mathcal{L}_{SCE} = \frac{1}{|\mathcal{V}|} \sum_{v_i \in \tilde{\mathcal{V}}} (1 - \frac{x_i^Tz_i}{\|x_i\| \cdot \|z_i\|})^{\gamma}, \]这里 \(\gamma > 1\) 是一个可调节的超参数. 可以看到 \(\gamma\) 的存在会减弱简单结点的影响, 更偏向困难的样本.
代码
[official]