Enhanced Doubly Robust Learning for Debiasing Postclick Conversion Rate Estimation

目录

• 概
• 符号说明
• 动机
• 本文算法
• 代码

Guo S., Zou L., Liu Y., Ye W., Cheng S., Wang S., Chen H., Yin D. and Chang Y. Enhanced doubly robust learning for debiasing post-click conversion rate estimation. In International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR), 2021.

概

先前的不论 EIB 还是 IPS, 抑或是 DR 都面临这 high-variance 的问题. 这篇文章主要是针对此问题进行的一个改进. 虽然这篇文章研究的是 Post-click Conversion Rate Estimation 的问题, 但是完全可以套用在 missing 的问题上, 所以下面就不把 \(p_{ui}\) 解释成用户是否点击, 而是观测到的概率.

符号说明

• \(\mathcal{U} = \{u_1, \ldots, u_N\}\), user;
• \(\mathcal{I} = \{i_1, \ldots, i_M\}\), item;
• \(\mathcal{D} = \mathcal{U} \times \mathcal{I}\);
• \(R \in \{0, 1\}^{N \times M}\), \(r_{u,i} = 1\) 表示 \(u\) 购买 \(i\), 否则表示不会购买;
• \(\hat{R} \in \{0, 1\}^{N \times M}\), predicted 交互矩阵;
• \(O \in \{0, 1\}^{N \times M}\), indicator matrix, \(o_{u,i} = 1\) 若 \(r_{u,i}\) 被观测到;
• \(\mathcal{O} = \{(u, i)| o_{u, i} = 1\}\);
• \(p_{u, i} = P(o_{u, i} = 1)\);
• \(\bm{x}_{u, i}\) 是 user \(u\), item \(i\) 的一些属性.

动机

1. 在有缺失数据的情况下, 一般来讲, 我们会选择最小化如下的损失:

   \[\mathcal{L}_{naive}(\hat{R}) = \frac{1}{|\mathcal{O}|} \sum_{(u, i) \in \mathcal{O}} e_{u, i}, \]

   但是一般来说, 在 MNAR (missing not at random) 的情况下,

   \[\mathbb{E}_{\mathcal{O}} [\mathcal{L}_{naive}(\hat{R})] \not = \frac{1}{|\mathcal{D}|} \sum_{(u, i) \in \mathcal{D}} e_{u, i} \triangleq \mathcal{L}_{ideal}(\hat{R}). \]

   这里

   \[e_{u, i} := \text{BCE}(r_{u,i}, \hat{r}_{u,i}); \]

2. 所以 DR 就提出了一种 low-bias 的估计:

   \[\tag{5} \mathcal{L}_{DR}(\hat{R}) = \frac{1}{|\mathcal{D}|} \sum_{(u, i) \in \mathcal{D}} [\hat{e}_{u, i} + \frac{o_{u, i} (e_{u, i} - \hat{e}_{u,i})}{\hat{p}_{u,i}}], \]

   其中 \(\hat{e}_{u, i}\) 是通过插值模型估计出来的, 而 \(\hat{p}_{u,i}\) 是通过一些别的方法估计出来的;

3. 可以证明 (5) 在 \(\hat{e}_{u, i} = e_{u,i} \: \forall (u, i)\) 或者 \(\hat{p}_{u, i} = p_{u,i}, \: \forall (u, i)\) 之一满足的情况下, 期望等于 \(\mathcal{L}_{ideal}(\hat{R})\), 故而是 low-bias 的;

4. 但是 (5) 的方差为:

   \[\tag{8} \mathbb{V}_{O} [\mathcal{L}_{DR}(\hat{R})] = \frac{1}{|\mathcal{D}|^2} \frac{p_{u,i} (1 - p_{u, i})}{\hat{p}_{u,i}^2} (e_{u, i} - \hat{e}_{u,i})^2. \]

   可见若 \(\hat{p}_{u, i}\) 估计的不好 (\(\hat{p}_{u, i}\) 很小), 会导致整体的方差很大;

5. 更糟糕的, 对于插值模型的拟合, 通常通过

   \[\mathcal{L}_e^{DR} = \sum_{(u, i) \in \mathcal{O}} \frac{(\hat{e}_{u, i} - e_{u, i})^2}{\hat{p}_{u,i}} \]

   来拟合, 但是在 \(\hat{p}_{u,i}\) 估计的不好的情况下, 上式的方差也是很大的.

本文算法

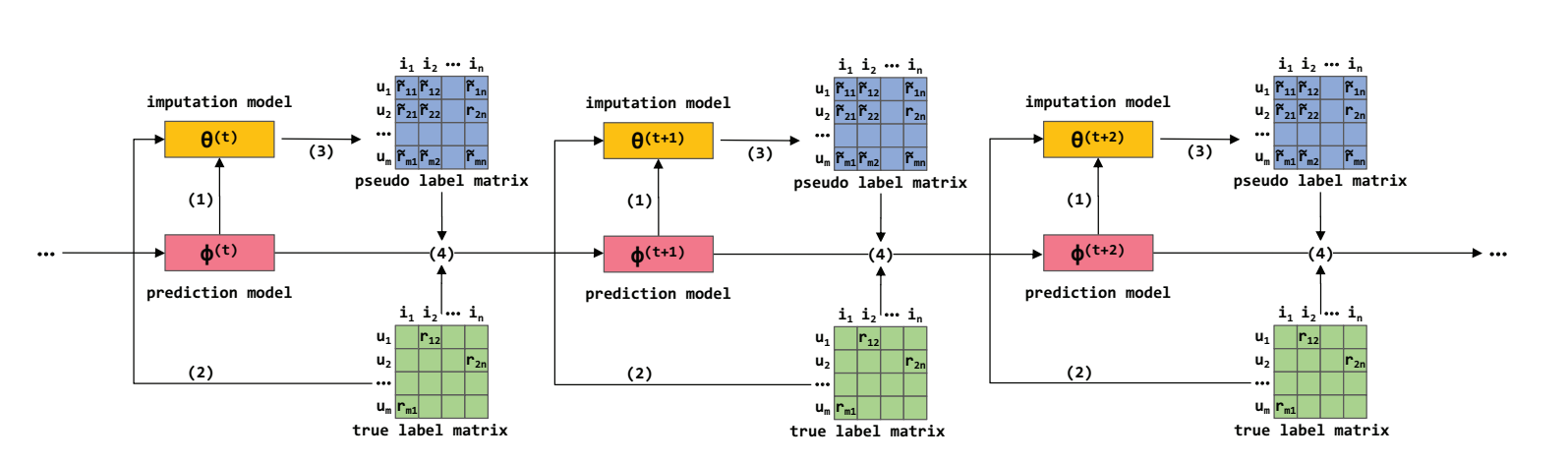
• Input: \(\mathcal{O}\), \(\mathcal{D}\), \(\hat{p}\);
• 利用插值模型 \(g_{\theta}(\bm{x}_{u, i})\) 来估计 \(\hat{e}_{u, i}\), 预测模型 \(g_{\phi}(\bm{x}_{u, i})\) 来预测 \(\hat{r}_{u,i}\), 二者的结构是一样的;
• 直到满足收敛条件:
  1. \(\theta \leftarrow \phi\) 用以校正 \(\theta\);
  2. 通过如下损失优化 \(\theta\) 多次:
     \[\tag{14} \mathcal{L}_e^{MRDR}(\theta) = \sum_{(u, i) \in \mathcal{O}} \frac{1 - \hat{p}_{u, i}}{\hat{p}^2_{u, i}} \cdot \text{BCE}(r_{u, i}, g_{\theta}(\bm{x}_{u, i})) + \lambda \|\theta\|_F^2; \]

  3. 生成伪标签 \(\tilde{r}_{u, i} = g_{\theta}(\bm{x}_{u, i}), \forall (u, i)\), 于是
     \[\hat{e}_{u, i} = \text{BCE}(\tilde{r}_{u, i}, \hat{r}_{u, i}). \]

  4. 利用伪标签训练 \(\phi\) 多次:
     \[\tag{15} \mathcal{L}_{r}^{MRDR}(\phi) =\sum_{(u, i) \in \mathcal{D}} [\hat{e}_{u, i} + \frac{o_{u, i} (e_{u, i} - \hat{e}_{u,i})}{\hat{p}_{u,i}}] + \mu \|\phi\|_F^2. \]

(14), (15) 的设计的思路如下:

1. (15) 就是 (5) 的一个自然延申;

2. 通过上一节的动机我们知道, (5) 的方差其实是挺大的, 在估计量 \(\hat{p}_{u, i}\) 无法改进的前提下, 作者希望拉近在 \(\hat{p}_{u, i}\) 很小的情况下 \(\hat{e}_{u,i}\) 的估计准确度. 故作者希望插值模型所估计的 \(\hat{e}_{u, i}\) 能够直接优化方差. 此时 (8) 和 (14) 的差别就在

   \[\tag{E} (e_{u, i} - \hat{e}_{u, i})^2 \rightarrow \text{BCE}(r_{u, i}, \tilde{r}_{u, i}) \]

   之上了.
   而之前的系数 \(\frac{1 - \hat{p}_{u,i}}{\hat{p}_{u, i}^2}\) 表达了我们对于 \(\hat{p}_{u, i}\) 很小的一个厌恶, 优化此损失会使得 \(g_{\theta}\) 特别照顾 \(\hat{p}_{(u, i)}\) 很小的情况;

3. 显然当 \(\text{BCE}(r_{u, i}, \tilde{r}_{u, i})\) 足够小的时候 \((e_{u, i} - \hat{e}_{u, i})^2 \rightarrow 0\);

4. 上述算法中的步骤 1: \(\theta \leftarrow \phi\), 作者是从 DoubleDQN [28] 中得到的启发.

注: 从消融实验来看, (E) 和 \(\theta \leftarrow \phi\) 校准操作并非必要的, 在有些情况下没有这些操作结果反而会稍微好一点, 不过加了这两个结果要稳定很多.

代码

[official]