Practical Data Poisoning Attack against NextItem Recommendation

目录

• 概
• 主要内容

Zhang H., Li Y., Ding B. and Gao J. Practical data poisoning attack against next-item recommendation. International World Wide Web Conferences (WWW), 2020.

概

设计一种 LOKI 的算法, 其伪造一些用户和行为, 使得用这些样本进行训练的推荐模型会偏向某些特定的物品进行推荐.

主要内容

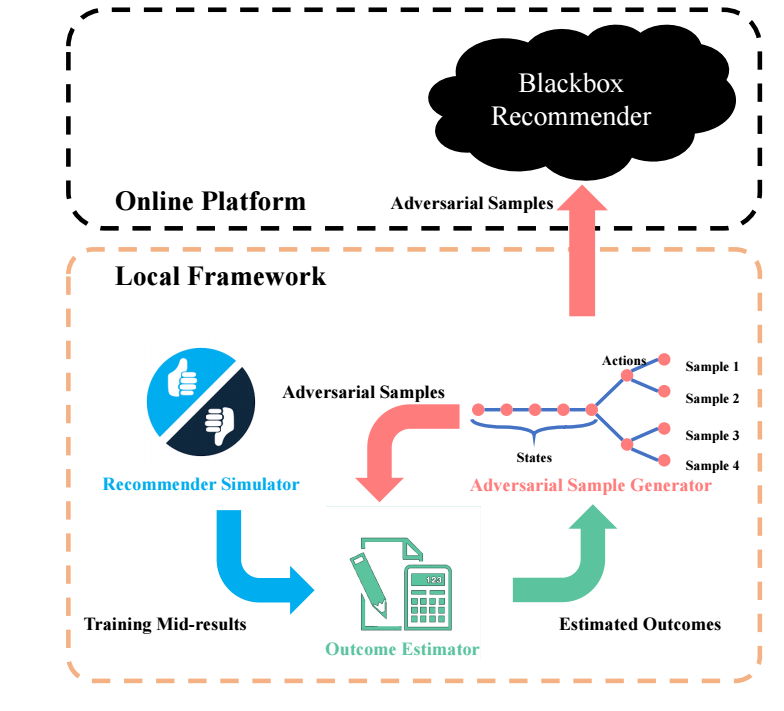
1. 假设所要攻击的推荐系统是个黑盒 (即模型, 参数, 训练方法是未知的); 于是认为地构造一个推荐系统: Recommender Simulator;
2. 利用强化学习 DQN 生成一些伪造的数据;
3. 为了保证这些伪造的数据能够使得模型对某些目标items有偏, 我们需要评估这些数据的影响并作为reward训练DQN;
4. 一种粗劣的方式是每次和原有数据进行一个结合, 然后重新训练 recommender simulator, 显然是非常耗时耗力的;
5. 故我们又引入了 Outcome Estimator 来评估这些伪造的数据的性能. 假设原有数据为 \(\{z_1, \cdots, z_N\}\), 此时最优的参数定义为:

\[\hat{\theta} := \mathop{\arg \min} \limits_{\theta} \frac{1}{N} \sum_{i=1}^N \mathcal{L}(z_i; \theta), \]

此时假设我们引入了一个伪造的数据 \(z_{\delta}\), 则

\[\hat{\theta}_{z_{\delta}}(\epsilon) := \mathop{\arg \min} \limits_{\theta} \frac{1}{N} \sum_{i=1}^N \mathcal{L}(z_i; \theta) + \epsilon \mathcal{L}(z_{\delta}; \theta). \]

自然地, 我们希望考察 \(\hat{\theta}_{z_{\delta}}(\frac{1}{N})\), 以及相应的损失变化量. 通过 here 可知:

\[\frac{d \hat{\theta}_{z_{\delta}}(\epsilon)}{d \epsilon} = -H_{\hat{\theta}}^{-1} \nabla_{\theta} \mathcal{L}(z_{\delta}; \hat{\theta}), \: H_{\hat{\theta}} := \frac{1}{N} \sum_{i=1}^N \nabla_{\theta}^2 \mathcal{L}(z_i; \hat{\theta}), \]

以及

\[\hat{\theta}_{z_{\delta}} (\frac{1}{N}) - \hat{\theta} \approx -\frac{1}{N} H_{\hat{\theta}}^{-1} \nabla_{\theta} \mathcal{L}(z_{\delta}; \hat{\theta}). \\ \]

6. 作者为了进一步判断 \(z_{\delta}\) 对推荐的影响, 定义 prediction score function \(f_{test}\) 用于 DQN 的学习, 则

\[\frac{d f_{test}(z_{u', v'}^{test}; \hat{\theta}_{z_{\delta}})}{d \epsilon} = \frac{d f_{test}(z_{u', v'}^{test}; \hat{\theta})}{d \hat{\theta}_{z_{\delta}}} \cdot \frac{d \hat{\theta}_{z_{\delta}}}{d \epsilon} = - \nabla_{\theta} f_{test} H_{\hat{\theta}}^{-1} \nabla_{\theta} \mathcal{L}(z_{\delta}; \hat{\theta}), \]

其中测试样本 \(z_{u', v'}^{test}\), 我们希望 item \(v'\) 被打高分以推荐给 user \(u'\).

注: 上面只是一个大致的流程,暂时不想了解 DQN, 细节就不讲了.
注: \(H\) 是通过 implicit Hessian-vector products 估计的.