概
对抗训练在 MF 上的一个应用, 区别是考虑的是对参数 \(\theta\) 的扰动. 所以更多的其实是偏泛化性, 而不是鲁棒性.

主要内容
基础
一般的 Matrix Factorization (MF) 方法可以理解构建
\[P = \{\bm{p}_u\}_{u \in \mathcal{U}}, Q = \{\bm{q}_i\}_{i \in \mathcal{I}},
\]
然后通过
\[\hat{y}_{ui} = \bm{p}_u^T \bm{q}_i
\]
进行偏好预测.
对于上述 \(\Theta = \{P, Q\}\) 的构造有不同的方法可以实现, 作者所考虑的是 BPR (Bayesian Personalized Ranking):
\[\tag{1}
\min_{\Theta}\: L_{BPR}(\mathcal{D}|\Theta) = \sum_{(u, i, j) \in \mathcal{D}} - \ln \sigma(\hat{y}_{ui} - \hat{y}_{uj}) + \lambda \|\Theta\|^2.
\]
其中
\[\mathcal{D} := \{(u, i, j)| i \in \mathcal{I}_u^+, j \in \mathcal{I} \setminus \mathcal{I}_u^+ \},
\]
\(\mathcal{I}_u^+\) 表示那些曾经和用户 \(i\) 发生过交互的物品的集合.
当我们把 \(\sigma(\hat{y}_{ui} - \hat{y}_{uj})\) 看成是概率
\[\mathbb{P}(i \succ j | u),
\]
即用户 \(u\) 在物品 \(i, j\) 前选择 \(i\) 而非 \(j\) 的概率, 那么 (1) 自然成为了一个似然损失.
对抗扰动
和普通的在图像上的对抗扰动不同, 作者考虑在参数 \(\Theta\) 上的扰动, 即
\[\Delta_{adv} := \arg \max_{\|\Delta\|_2 \le \epsilon} L_{BPR}(\mathcal{D}|\Theta + \Delta).
\]
一般来说, 当 \(\epsilon\) 比较小的时候, 模型的结果应该相差不大, 但是实际情况是:
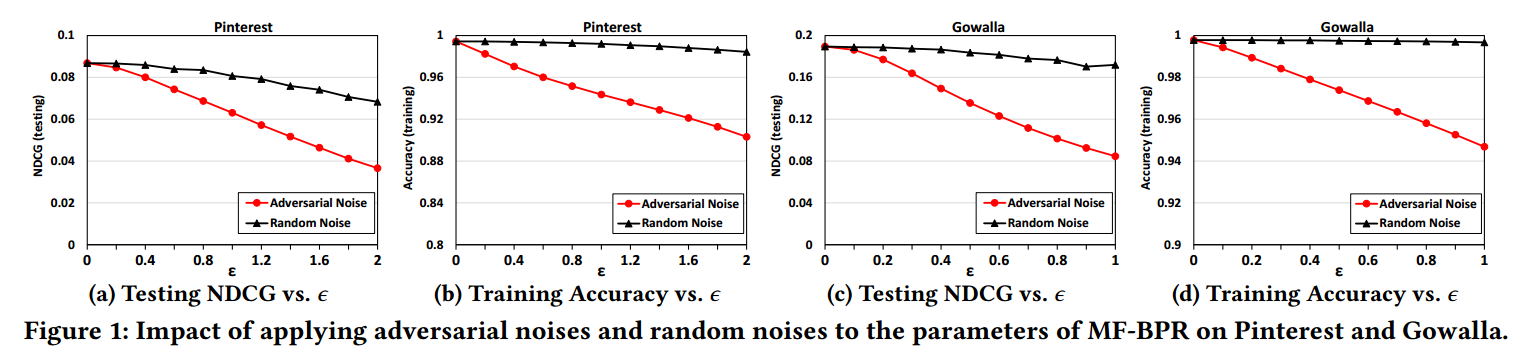
模型在训练集上的确对于扰动不敏感, 但是在测试集, 即没见过的样本上表现相当糟糕. 所以可以认为现有方法所训练出来的模型是非常鲁棒的.
对抗训练
故本文提出以下的对抗训练, 用于增强鲁棒性:
\[L_{APR} (\mathcal{D}|\Theta) = L_{BPR}(\mathcal{D}|\Theta)
+\lambda L_{BPR}(\mathcal{D}|\Theta + \Delta_{adv}) + \lambda_{\Theta} \|\Theta\|_2^2. \\
\]
在实际中, \(\Delta_{adv}\) 是利用 FGSM 估计得到的:
\[\Delta_{adv} = \epsilon \frac{\Gamma}{\|\Gamma\|_2}, \: \Gamma= \frac{\partial L_{adv}}{\partial \Delta}, \\
L_{adv}(\mathcal{D}|\Delta) = \sum_{(u, i, j) \in \mathcal{D}} \ell_{adv} ((u, i, j) | \Delta), \\
\ell_{adv}((u, i, j)|\Delta) := -\lambda \ln (\sigma(\hat{y}_{ui}(\hat{\Theta} + \Delta)- \hat{y}_{uj}(\hat{\Theta} + \Delta) )).
\]
注: 作者训练的时候实际上用的是 mini-batch 的 \(\mathcal{D}'\) 替代 \(\mathcal{D}\).
细节
- 模型用标准训练后的模型进行初始化;
- embedding size: 64; (但实验发现是越大越好, 作者没有探索 \(>64\)的情况)
- optimizer: Adagrad;
- batch size: 512;
- \(\epsilon=0.5, \lambda = 1\).
代码
[official]