Pareto MultiTask Learning

目录

• 概
• 主要内容
  • 多任务的可行下降方向
  • 受限情况下的可行下降方向
    • 初始可行解
    • 可行下降方向
  • 更高效的对偶算法
• 代码

[1] Lin X., Zhen H., Li Z., Zhang Q. and Kwong S. Pareto multi-task learning. In Advances in Neural Information Processing Systems (NIPS), 2019.

[2] Fliege J. and Svaiter B. F. Steepest descent methods for multicriteria optimization. Mathematical Methods of Operations Research, vol. 51, pp. 479–494, 2000.

概

对于 \(m\) 个任务

\[\mathcal{L}_1(\theta), \mathcal{L}_2(\theta), \cdots, \mathcal{L}_m (\theta) \]

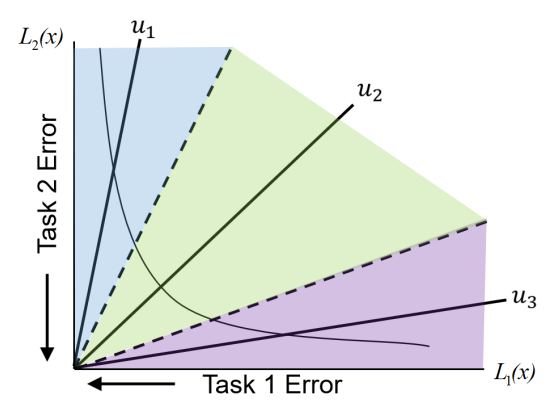
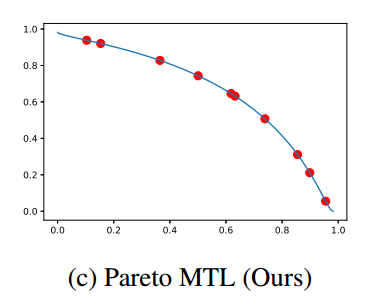
而言, 能够达到 Pareto 最优自然是好的, 但是 Pareto 最优的 \(\theta\) 往往不是唯一的, 那么它们之前又孰优孰劣? 本文尝试预先设定 \(K\) 个方向 \(\bm{u}_1, \bm{u}_2, \cdots, \bm{u}_K \in \mathbb{R}^m\), 然后对于每个方向和区域, 并行地找到各自地 Pareto 最优点, 对这些 Pareto 最优点进行评估, 找到一个更加合适的.

主要内容

正如上述, 我们的目标是找到

\[\min_{\theta} \: \mathcal{L}(\theta) = [\mathcal{L}_1(\theta), \cdots, \mathcal{L}_m (\theta)]^T \]

的一组 Pareto 最优解.

我们的基本策略是采取

\[\theta_{t+1} = \theta_t + \eta d_t \]

的梯度更新方式, 这要求 \(d_t\) 最好对于所有的任务而言都是可行的下降方向, 即

\[d_t^T\nabla_{\theta} \mathcal{L}_i \le 0, \: \forall i. \]

我们先介绍不加 \(\bm{u}\) 下搜寻可行下降方向的策略, 再介绍添加 \(\bm{u}\) 限制的情况.

多任务的可行下降方向

我们可以通过求解

\[\tag{1} \begin{array}{rl} \min_{d, \alpha} & \alpha + \frac{1}{2} \| d \|^2 \\ \mathrm{s.t.} & d^T \nabla \mathcal{L}_i (\theta_t) \le \alpha, \: i=1,2,\cdots, m, \end{array} \]

来寻找 \(d_t\). 有以下性质:

Lemma1:

1. 如果 \(\theta_t\) 是 Pareto critical 的, 则 \(d_t = 0 \in \mathbb{R}^n, \alpha_t = 0\);
2. 否则

\[\alpha_t \le -\frac{1}{2} \|d_t\|^2 < 0 \\ d_t^T \nabla \mathcal{L}_i (\theta_t) \le \alpha_t < 0, \: i=1,2,\cdots, m, \]

此时 \(d_t\) 是一个可行的下降方向.

注: Pareto critical [2] 是指不存在 \(v \in \mathbb{R}^n\)

\[v^T \nabla_{\theta} \mathcal{L}_i (\theta) < 0, \: i=1,2,\cdots, n. \]

---

proof:

case 1: 显然此时 \(\alpha = 0\), 因为 \(d = 0\);
case 2: 由于 $\alpha = 0, d = 0 $ 为一可行解, 故最优解应当满足

\[\alpha + \frac{1}{2} \|d\|^2 < 0. \]

---

受限情况下的可行下降方向

此情况是为了同时找到一组尽量分散的 Pareto 最优解, 这些解分布在预先规划的区域:

\[\Omega_k = \{\bm{v} \in \mathbb{R}_+^m | \bm{u}_j^T \bm{v} \le \bm{u}^T_k \bm{v}, \: \forall j = 1,2,\cdots, K\}. \]

即:

\[\begin{array}{rl} \min_{\theta} & \mathcal{L}(\theta) = [\mathcal{L}_1(\theta), \cdots, \mathcal{L}_m (\theta)]^T \\ \text{s.t.} & \mathcal{L}(\theta) \in \Omega_k \Leftrightarrow \mathcal{G}_j(\theta) := (\bm{u}_j - \bm{u}_k)^T \mathcal{L}(\theta_t) \le 0, \: \forall j = 1,2,\cdots, K. \end{array} \]

将 \(\bm{u}\) 看成是施加给任务的权重, 我们希望最优值损失的分布是按照我们所期望的那样分布的.

初始可行解

注意到, 此时随机参数化得到的参数 \(\theta_r\) 可能不再可行域中, 故首先需要进行一个调整:

\[\min_{\theta_0} \: \|\theta_0 - \theta_r\|^2 \: \text{s.t.} \mathcal{L}(\theta_0) \in \Omega_k. \]

采用类似 (1) 的方式:

\[(d_t, \alpha_t) = \mathop{\text{argmin}} \limits_{d \in \mathbb{R}^n, \alpha} \: \alpha + \frac{1}{2} \|d\|^2, \quad \text{s.t.} \: d^T\nabla \mathcal{G}_j(\theta) \le \alpha, \: j \in I(\theta). \]

其中

\[I(\theta) = \{j | \mathcal{G}_j (\theta) \ge 0, j=1,2,\cdots, K\} \]

代表激活的约束.

可行下降方向

我们可以采用和 (1) 类似的方法找到合适的下降方向:

\[\tag{2} \begin{array}{rl} \min_{d, \alpha} & \alpha + \frac{1}{2} \| d \|^2 \\ \mathrm{s.t.} & d^T \nabla \mathcal{L}_i (\theta_t) \le \alpha, \: i=1,2,\cdots, m \\ & d^T \nabla \mathcal{G}_j (\theta_t) \le \alpha, \: j \in I_{\epsilon} (\theta_t). \end{array} \]

其中

\[I_{\epsilon}(\theta) = \{j | \mathcal{G}_j (\theta) \ge \epsilon, j=1,2,\cdots, K\} \]

显然, 这也有和 Lemma1 类似的结论:

Lemma2:

1. 如果 \(\theta_t\) 是 Pareto critical 的, 则 \(d_t = 0 \in \mathbb{R}^n, \alpha_t = 0\);
2. 否则

\[\alpha_t \le -\frac{1}{2} \|d_t\|^2 < 0 \\ d_t^T \nabla \mathcal{L}_i (\theta_t) \le \alpha_t < 0, \: i=1,2,\cdots, m \\ d_t^T \nabla \mathcal{G}_j (\theta_t) \le \alpha_t < 0, \: j \in I_{\epsilon}(\theta_t), \]

此时 \(d_t\) 是一个可行的下降方向. 证明思路是一样的, 不多赘述了.

更高效的对偶算法

当任务的参数 \(\theta\) 维度比较高的时候, 求解 (1) (2) 都需要求解一个高维的线性规划问题, 这会比较费时且效果可能不是特别好, 所以可以将其转换为对偶问题求解.

用拉格朗日乘子可得(记\(U = [u_1, \cdots, u_m], u_i := \nabla \mathcal{L}_i\), 类似的\(G\) 为\(\mathcal{G}\)所对应的矩阵)

\[L(\lambda, \beta; d, \alpha) = \alpha + \frac{1}{2}\|d\|^2 + \lambda^T(U^T d - \alpha \bm{1}) + \beta^T (G^T d - \alpha \bm{1}). \]

于是

\[\tag{3} \begin{array}{ll} \mathrm{inf}_{d, \alpha} L = \mathrm{inf}_{\alpha} [1 - \sum_i \lambda_i - \sum_j \beta_j ] \alpha +\mathrm{inf}_{d} [\frac{1}{2}\|d\|^2 + \lambda^T U^T d + \beta^T G^T d], \end{array} \]

显然只有在

\[\sum_i \lambda_i + \sum_j \beta_j = 1 \\ d = -U\lambda -G\beta \]

(3) 才有意义 (即 \(> -\infty\)). 故最后对偶问题为:

\[\begin{array}{rl} \max & -\frac{1}{2} \|\sum_i \lambda_{i =1}^m \nabla \mathcal{L}_i (\theta)+ \sum_{j \in I_{\epsilon}(\theta)} \beta_j \mathcal{G}_j (\theta)\|^2 \\ \text{s.t.} & \sum_i \lambda_i + \sum_j \beta_j = 1 \\ & \lambda_i \ge 0 \: \forall i = 1,2,\cdots, K \\ & \beta_j \ge 0 \: \forall j \in I_{\epsilon}(\theta). \end{array} \]

这个结论其实和 MGDA, MGDA-UB 的结果是一样的.

注: 各线性规划问题的求解思路和 MGDA-UB 中的是一样的.

代码

原文代码