概
FM 通过
\[\sum_{j_1=1}^n \sum_{j_2 = j_1 + 1}^n \bm{w}_{j_1}^T \bm{w}_{j_2} x_{j_1}x_{j_2}
\]
来构建特征间的交互关系, 同时避免了数据稀疏的问题. 本文所提出的 FFM 则是在基础上上引入了 field 的概念.
主要内容
| Clicked | Publisher (P) | Advertiser (A) | Gender (G) |
|---|---|---|---|
| Yes | ESPN | Nike | Male |
如上表所示, 对于 FM 而言, 其通过如下方式进行特征交互
\[\bm{w}_{\text{ESPN}}^T \bm{w}_{\text{NIKE}}
+\bm{w}_{\text{ESPN}}^T \bm{w}_{\text{Male}}
+\bm{w}_{\text{NIKE}}^T \bm{w}_{\text{Male}},
\]
作者认为, 令诸如出版社既要和广告商又要和性别特征进行交互, 仅依赖一个特征\(\bm{w}_{\text{ESPN}}\)是不够的, 而是应该:
\[\bm{w}_{\text{ESPN, A}}^T \bm{w}_{\text{NIKE, P}}
+\bm{w}_{\text{ESPN, G}}^T \bm{w}_{\text{Male, P}}
+\bm{w}_{\text{NIKE, G}}^T \bm{w}_{\text{Male, A}}.
\]
一般地, 可以表示为
\[\phi_{\text{FFM}}(\bm{w}, \bm{x}) = \sum_{j_1=1}^n \sum_{j_2 = j_1 + 1}^n \bm{w}_{j_1, f_2}^T \bm{w}_{j_2, f_1} x_{j_1} x_{j_2}.
\]
即两个特征\(x_{j_1}, x_{j_2}\)交互时, 采用特定的域特征.
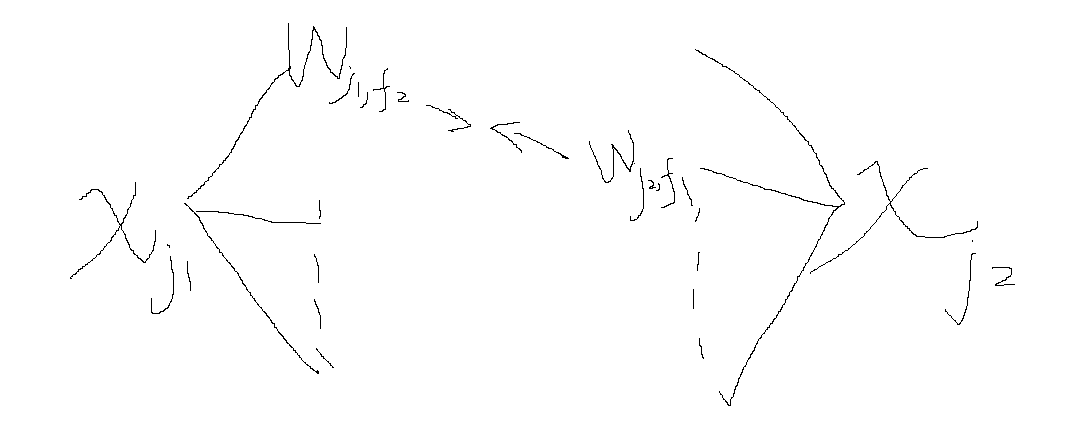
因为分割了很多域, 所以通常\(\bm{w}_{j, f}\)会比 FM 中 \(\bm{w}\)的维度小得多.
最后通过如下损失进行优化:
\[\min_{\bm{w}} \frac{\lambda}{2} \|\bm{w}\|_2^2 + \sum_{i=1}^m \log (1 + \exp (- y_i \phi_{\text{FFM}}(\bm{w}, \bm{x}_i))).
\]
注: 关于如何确定域, 作者讨论了三种情况: 类别, 数值 以及诸如语句这种单一field的类型. 感觉这个域就是一个特征的总称呐.