What Neural Networks Memorize and Why: Discovering the Long Tail via Influence Estimation

目录

• 概
• 主要内容
  • 一种简便的估计方法
  • 被记忆的样本所产生的边际效用
  • 不同网络结构下的实验
  • 最后一次是否足够用于记忆
  • 一些示例

Feldman V. and Zhang C. What neural networks memorize and why: discovering the long tail via influence estimation. In Advances in Neural Information Processing Systems (NIPS), 2020.

概

关于这篇文章中所提及的对于长尾分布中小样本记忆的必要性的实验说明.

主要内容

在之前的工作中, 作者指出, 对于长尾分布中的小样本数据, 算法\(\mathcal{A}\)尝试去记忆这些小样本数据对于提高泛化性是非常重要的.

我们定义在算法\(\mathcal{A}\)和训练集\(S\)中, 删除样本\((x_i, y_i) \in S\)对于样本\(z = (x, y)\)的影响:

\[\mathrm{infl}(\mathcal{A}, S, i, z):= \mathbb{P}_{h \sim \mathcal{A}(S)}[h(x) = y] - \mathbb{P}_{h \sim \mathcal{A}(S\setminus i)}[h(x) = y], \]

这里$S\setminus i \(表示从数据集\)S\(中删除\)(x_i, y_i)\(. 显然上面的值越大, 影响越大, 直观来说, 倘若算法\)\mathcal{A}\(没有在训练的时候见过样本\)(x_i, y_i)\(则所拟合的函数\)h\(很难正确判断\)(x, y)\(. 这种情况往往发生在, 样本\)(x_i, y_i), (x, y)$相近且都是小样本的情况下.

当\((x, y) = (x_i, y_i)\)的时候, 可以理解为拟合该样本是否需要'记忆'它, 其值为

\[\mathrm{mem}(\mathcal{A}, S, i) = \mathrm{infl}(\mathcal{A},S, i, (x_i, y_i)). \]

一种简便的估计方法

想要对每一对样本都估计出上述的值是非常耗时的, 因为这意味这为了每一个值我们要反复运行算法多次以保证结果的方差不会太大.
文中作者给出了一个较为快速的估计方式:

\[\tag{1} \mathrm{infl}(\mathcal{A}, S, i, z) := \mathbb{E}_{I \sim P([n]\setminus \{i\}, m - 1)} [\mathrm{infl}(\mathcal{A}, S_{I \cup \{i\} } , i, z)]. \]

这里:

\[[n] = \{1, 2,\cdots, n\} \\ S_I = (x_i, y_i)_{i \in I}, \]

对于任意的\(J \subset [n]\), \(P(J, m)\)表示从\(J\)中等可能地不放回地抽取\(m\)次过程的分布.

有如下引理来衡量该方法的估计的方差:

如果光看公式(1)可能还是觉得超级超级麻烦的, 但是实际的算法是从证明过程中启发得到的, 实际的算法如下:

1. 从\([n]\)中采样大小为\(m\)的子集\(t\)次: \(I_1, I_2, \cdots, I_t\).
2. 各自在\(S_{I_k}\)上训练得到拟合的函数\(h_k, k=1,2,\cdots, t\).

接下来, 对于任意的\(i\), 将上述子集分割成\(A_i, B_i\):

\[A_i = \{k: i \in I_k\}, \\ B_i = \{k: i \not \in I_k\}. \]

则

\[\mathrm{infl}_m(\mathcal{A}, S, i, z) := \frac{|\{k \in A_i: h_k(x) = y\}|}{|A_i|} - \frac{|\{k \in B_i: h_k(x) = y\}|}{|B_i|}. \]

显然, 该算法只要求我们估计模型共\(t\)次, 虽然文中采取的\(t=2000\)也是相当耗时的.

如果通过原文的证明可以发现, \(\frac{|\{k \in A_i: h_k(x) = y\}|}{|A_i|}\)和 \(\frac{|\{k \in B_i: h_k(x) = y\}|}{|B_i|}\)分别是

\[\mathbb{E}_{I \sim P([n]\setminus \{i\}, m - 1)} [\mathbb{P}_{h \sim \mathcal{A}(S_{I\cup \{i\}})}[h(x) = y]] \]

和

\[\mathbb{E}_{I \sim P([n]\setminus \{i\}, m - 1)} [\mathbb{P}_{h \sim \mathcal{A}(S_{I})}[h(x) = y]] \]

的估计.

注: 对于任意\(|A_i|\)或者\(|B_i\)为0的, 对应的估计取为\(\frac{1}{2}\).

被记忆的样本所产生的边际效用

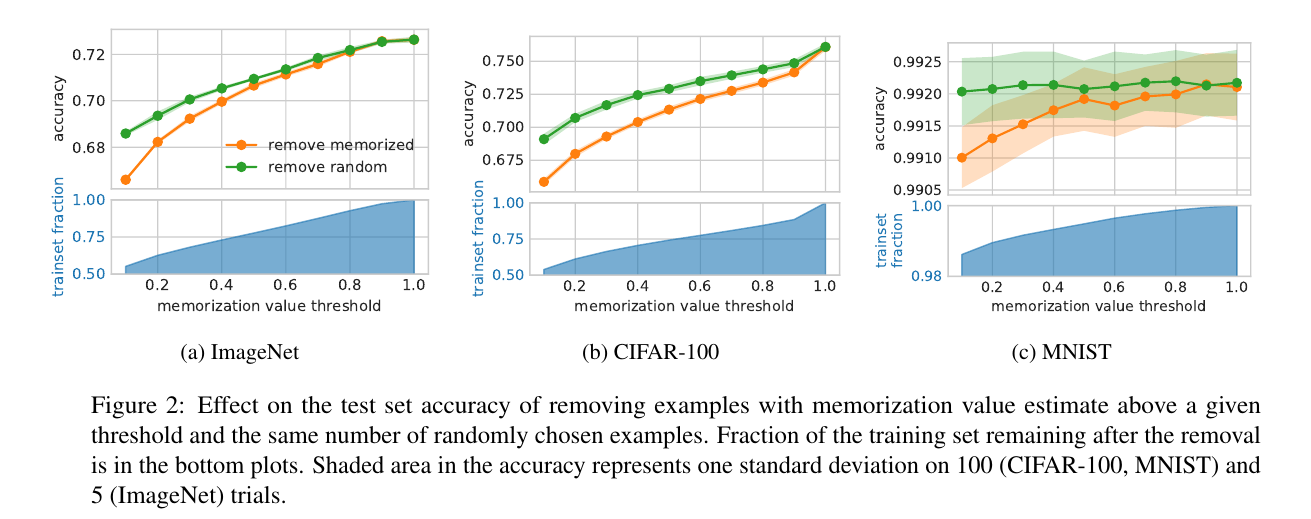
如果这些小样本非常重要, 那么如果我们在拟合的时候不去记忆它们应当会产生严重的后果.

1. 橙色的线就是舍去那些\(\mathrm{mem}\)值大于一定值后的测试精度;
2. 蓝色线表示从整个训练集中随机舍去相同数量的样本后的测试精度.
   显然这些小样本非常重要.

注: 蓝色部分表示舍弃这些样本后训练集中还剩下样本的比例, 可以发现大部分样本都是普通的(特别是对于MNIST这种简单的数据集而言).

不同网络结构下的实验

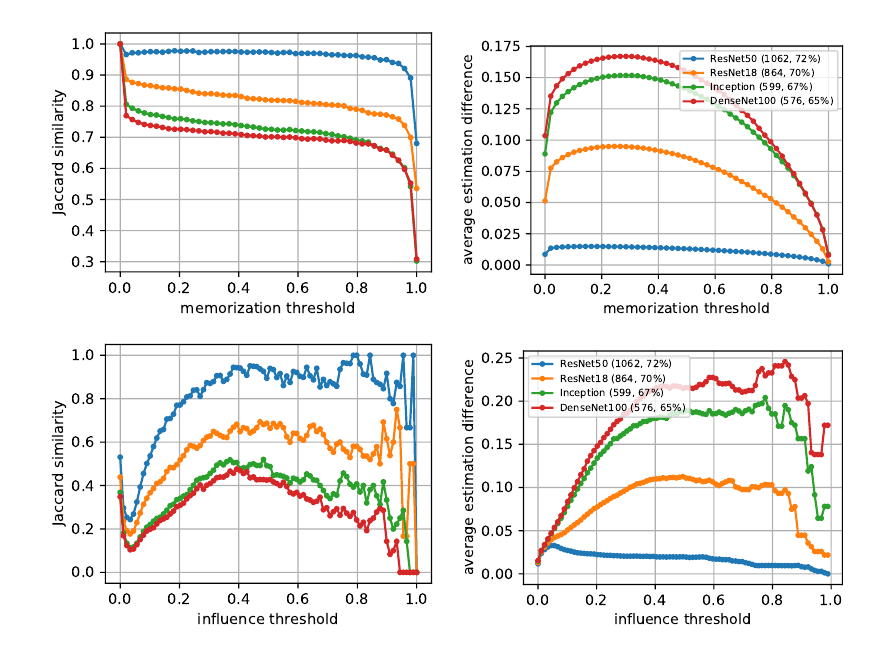
一个很有意思的问题是: 不同的网络结构(随机因素)对于小样本的记忆功能是否是一致的呢?
文中用了两个指标去衡量不同值的差别, 越大说明越温和.

需要注意的是, 图中的线条都是各网络 vs ResNet50, 另外 ResNet50 vs ResNet50 表示两个不同的初始化.
可以发现, 不同的网络结构的确具有不同的记忆特性, 这些差别主要集中在高\(\mathrm{infl}\)上, 即那些特别的小样本上. 可以这样理解, 由于这些样本不是通过语义特征来区分的, 所以不同的结构和随机因素便会倾向于不同的记忆方式.

最后一次是否足够用于记忆

很多预训练模型都是将最后一层前作为特征提取器, 之后的作为分类器. 那么问题是, 固定前面的编码器,
仅凭后面的分类器能否记忆这些特殊的小样本呢, 实验给出的答案是不能.

一些示例