Avoiding False Local Minima by Proper Initialization of Connections

目录

• 概
• 主要内容
  • 输入层-隐藏层
  • 隐藏层-输出层

Wessels L. F. A. and Barnard E. Avoiding False local minima by proper initialization of connections. In IEEE Transactions on Neural Networks, 1992.

概

避免局部最优的一种初始化方法, 文中给出的‘合适的'初始化方法的准则还挺有道理.

主要内容

本文主要考虑单隐层的情形, 即

\[f(x) = \sum_{j=1}^H v_j h(\sum_{i=1}^n w_{ij}x_i + w_{0jj}) + v_0. \]

其中\(h(\cdot)\)表激活函数.

下面将分别讨论输入层-隐藏层以及隐藏层-输出层的权重初始化的一些准则.

输入层-隐藏层

对于隐藏层的某个结点而言,

\[\tag{1} y = w_0 + w_1x_1 + \cdots + w_nx_n. \]

我们希望这些结点避免以下情况的发生:

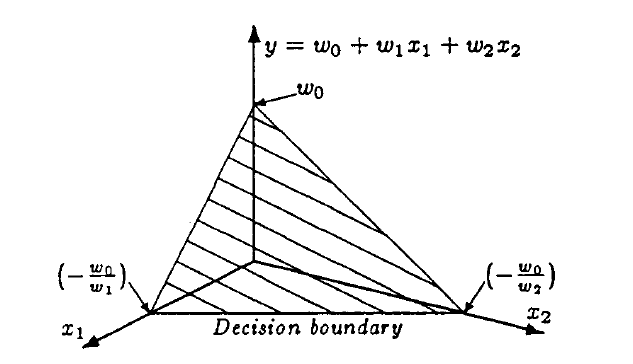
1. 离群的结点: 即大部分样本点距离分类平面(边界) \(y(x) = w^T x + w_0\) 都很远,
   这会导致这些样本点对应的\(y(x)\)要么是很大要么是非常小.
   前者会导致弱化其它结点的影响, 后者会导致这个结点意义不大;
2. 重复的结点: 如果两个结点的分类平面非常接近, 容易产生冗余的结果;
3. 结点存在死区(即落入该区域的所有结点都是inactive的).

我们要遵循以下原则来避免上述的几点问题:

1. 决策平面应当在样本空间中合理划分;
2. 决策平面的朝向(\(w\))应当尽可能有所变换;
3. 样本空间的每个区域都应该有至少一个结点是active的.

注: 因为以前的论文大都使用sigmoidal类的激活函数, 所以一般来说 \(y > 0\)被认为是active的, 反之是inactive的.

对于1, 2, 作者希望权重向量 \(\bm{w}_i, i = 1,2,\cdots, H\)之间在空间中是均匀分布的(注意该向量包括偏执\(w_0\)), 比如在二维空间中, 极坐标系下, \(\bm{w}_i = (r_i\cos \theta_i, r_i\sin\theta_i)\),

\[\theta_i = \left \{ \begin{array}{ll} \frac{\pi}{H} \cdot i & i \: \text{odd} \\ \frac{\pi}{H} \cdot i + \pi & \: i \: \text{even}. \end{array} \right . \]

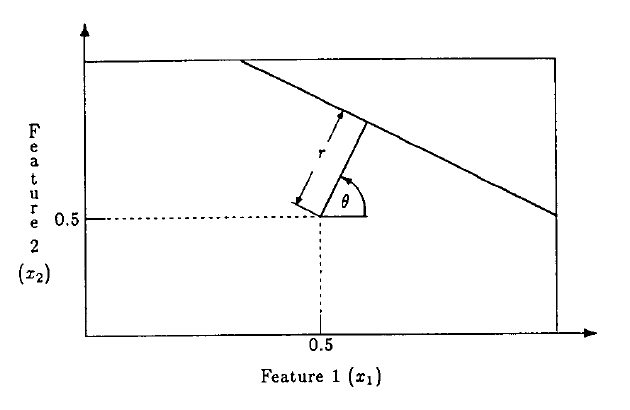
注: 文中实际上选择的是 \(\bm{w}_i = (r\cos \theta_i + 0.5, r\sin\theta_i + 0.5)\), 因为其假设 \(x_i \in [0, 1]\).

为了进一步完善第一点(说是为了最大化方差但是这个不是那么直观), 向量的模长\(r_i\)为

\[r_i = \frac{1}{i}r_1, \: r_1 = 0.5. \]

为了保证第三点, 对于\(\bm{w}_i\)的朝向问题进行一个限制, 其需要保证 \(y(0) > 0\), 实际上就是需要满足\(w_0>0\).

隐藏层-输出层

作者没有明确给出构造方法, 只是说太大或者太小都不太好.
且建议\(v_i\)大小一致以保证对各结点没有偏见.