概
本文介绍AUGMIX算法——对现有的的一些augmentation方法进行混用, 并构建了一个新的损失函数.
主要内容


其中(mathrm{Dirichlet})为狄利克雷分布.
通过实验指出, Augmentation的混用(增加样本的多样性)以及损失函数的设计都是有利于稳定性以及不确定度的.
[mathbf{JS}(p_{orig};p_{augmix1};p_{augmix2}) = frac{1}{3} (mathbf{KL}[p_{orig}|M]+mathbf{KL}[p_{augmix_1}| M] + mathbf{KL}[p_{augmix_2}| M]),
]
其中(M:= (p_{orig} + p_{augmix1}+p_{augmix2})/3).
实验的指标
Clean Error: 指在干净样本上的错误率;
(E_{c,s}): 指在困难等级(1 le s le 5), 污染(摄动, corruption) (c)下的错误率;
(CE_c = sum_{s=1}^5E_{c,s}/ sum_{s=1}^5 E_{c,s}^{mathrm{Alexnet}});
(mCE): (mathrm{mean}_{c} : CE_{c});
flip probability (FP): 微小摄动下, 样本预测类改变的概率; 如何估计?
(mFP): the mean flip probability (对于所有的(c)); -衡量鲁棒性;
(mFR): (mFP) 比上 Alexnet 的(mFP) ;
不确定估计:
[sqrt{mathbb{E}_C [mathbb{P}(Y = hat{Y} | C=c)-c)^2]},
]
其中(C)为预测(hat{Y})正确的(confidence)(如果输出是一个概率向量, 那么就应当是对应类别的概率), 采用如下方式估计:
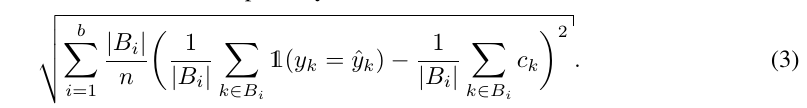
其中(B_i), 是我们按照confidence的序来将测试样本分割为((B_1, B_2, ldots, B_b)).