题意:给定平面上两类同样多的点,要求输出一种方案使得所有匹配的点的连线两两不相交。
解法:考虑到下面的一般情况:
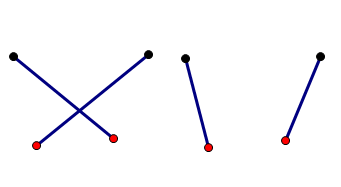
可以很容易的证明两条交叉边的距离和一定大于两条不交叉的距离和,因此问题转化为只要原图中存在交叉边,那么就可以找到更小的匹配的方式使得总距离更小。使用KM算法求出最小权值匹配输出匹配方案即可。
代码如下:
#include <cstdlib> #include <cstring> #include <cstdio> #include <algorithm> #include <iostream> #include <cmath> using namespace std; int N; double w[105][105]; int sx[105], sy[105]; double lx[105], ly[105]; double slack[105]; int match[105]; struct Node { int x, y; }c[105], t[105]; double dist(const Node &a, const Node &b) { return sqrt((a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y)); } void build() { for (int i = 1; i <= N; ++i) { for (int j = 1; j <= N; ++j) { w[i][j] = -dist(c[i], t[j]); } } } int path(int u) { sx[u] = 1; for (int i = 1; i <= N; ++i) { if (sy[i]) continue; double t = lx[u] + ly[i] - w[u][i]; if (fabs(t) < 1e-6) { // 如果这个值等于0 sy[i] = 1; if (!match[i] || path(match[i])) { match[i] = u; return true; } } else { slack[i] = min(slack[i], t); } } return false; } void KM() { memset(match, 0, sizeof (match)); fill(ly, ly+105, 0); fill(lx, lx+105, 0); for (int i = 1; i <= N; ++i) { for (int j = 1; j <= N; ++j) { // 为i选择一个最大的权值 lx[i] = max(lx[i], w[i][j]); } } for (int i = 1; i <= N; ++i) { // 每一次都要为i找到一条增广路 fill(slack, slack+105, 1e30); while (1) { memset(sx, 0, sizeof (sx)); memset(sy, 0, sizeof (sy)); if (path(i)) break; double d = 1e30; for (int j = 1; j <= N; ++j) { if (!sy[j]) d = min(d, slack[j]); } for (int j = 1; j <= N; ++j) { if (sx[j]) lx[j] -= d; if (sy[j]) ly[j] += d; else slack[j] -= d; } } } for (int i = 1; i <= N; ++i) { for (int j = 1; j <= N; ++j) { if (match[j] == i) { printf("%d\n", j); break; } } } } int main() { while (scanf("%d", &N) != EOF) { for (int i = 1; i <= N; ++i) { scanf("%d %d", &c[i].x, &c[i].y); } for (int i = 1; i <= N; ++i) { scanf("%d %d", &t[i].x, &t[i].y); } build(); KM(); } return 0; }