转自:https://github.com/SmirkCao/Lihang
最近又捡起了李航老师的《统计学习方法》开始啃,之前因为干货太多一看就困索性放弃(捂脸~),突然在知乎上看到有大神的总结,希望大神能带我飞哈哈。
[TOC]
- GitHub的markdown公式支持一般, 推荐使用Chrome插件TeX All the Things来渲染TeX公式, 本地Markdown编辑器推荐Typora.
- math_markdown.pdf为math_markdown.md的导出版本, 方便查看使用, markdown版本为最新版本, 基本覆盖了书中用到的数学公式的LaTeX表达方式。
前言
这部分内容并不对应<统计学习方法>中的前言, 书中的前言写的也很好, 引用如下:
1. 在内容选取上, 侧重介绍那些最重要, 最常用的方法, 特别是关于分类与标注问题的方法.
2. 力图用统一框架来论述所有方法, 使全书整体不失系统性.
3. 适用于信息检索及自然语言处理等专业大学生, 研究生.
另外还有一点要注意作者的工作背景
作者一直从事利用统计学习方法对文本数据进行各种智能性处理的研究, 包括自然语言处理、信息检索、文本数据挖掘。
- 每个人都有适合自己的理解方式, 对同样的内容, 会有不同的理解
- 书如数据, 学如训练, 人即模型.
如果用我这个模型来实现相似度查找, 和李老师这本书神似的就是<半导体光电器件>了, 只可惜昔时年少, 未曾反复研读.
希望在反复研读的过程中, 将整个这本书看厚, 变薄. 这个系列的所有的文档, 以及代码, 没有特殊说明的情况下"书中"这个描述指代的都是李航老师的<统计学习方法>. 其他参考文献中的内容如果引用会给出链接.
在Refs中列出了部分参考文献, 有些参考文献对于理解书中的内容是非常有帮助的, 关于这些文件的描述和解释会在参考部分对应的Refs/README.md 中补充.
另外, 李航老师的这本书, 真的很薄, 但是几乎每句话都会带出很多点, 值得反复研读.
书中在目录之后有个符号表, 解释了符号定义, 所以如果有不理解的符号可以过来查表. 另外, 每个算法,示例结束之后会有一个◼️, 表示这个算法或者例子到此结束.
关于对数底数
读书的时候经常会有关于对数底数是多少的问题, 有些比较重要的, 书中都有强调. 有些没有强调的, 通过上下文可以理解. 另外, 因为有换底公式, 所以, 底具体是什么关系不是太大, 差异在于一个常系数. 但是选用不同的底会有物理意义和处理问题方面的考虑, 关于这个问题的分析, 可以看PRML 1.6中关于熵的讨论去体会.
另外关于公式中常系数的问题, 如果用迭代求解的方式, 有时对公式做一定的简化, 可能会改善收敛速度. 个中细节可以实践中慢慢体会.
关于篇幅
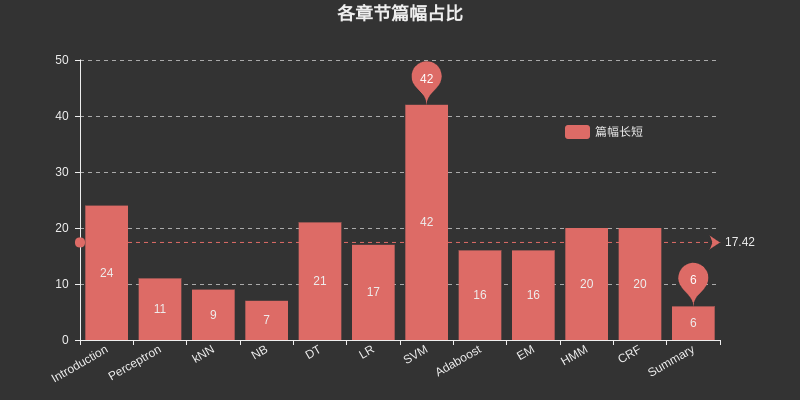
这里插入个图表,列举了各个章节所占篇幅,其中SVM是大部头,占了很大的篇幅,另外DT,HMM,CRF也占了相对较大的篇幅。
章节之间彼此又有联系,比如NB和LR,DT和AdaBoost,Perceptron和SVM,HMM和CRF等等,如果有大章节遇到困难,可以回顾前面章节的内容,或查看具体章节的参考,一般都给出了更详细的参考文献。
CH01 统计学习方法概论
Introduction
统计学习方法三要素:
- 模型
- 策略
- 算法
CH02 感知机
Perception
- 感知机是二类分类的线性分类模型
- 感知机对应于特征空间中将实例划分为正负两类的分离超平面.
CH03 k近邻法
KNN
- kNN是一种基本的分类与回归方法
- k值的选择, 距离度量及分类决策规则是kNN的三个基本要素
CH04 朴素贝叶斯法
NB
- 朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法.
- $IID ightarrow$输入输出的联合概率分布
- $Bayes ightarrow$后验概率最大的输出
- x的某种组合在先验中没有出现的情况, 会出现概率为0的情况, 对应平滑处理方案 $$P_lambda(X^{(j)}=a_{jl}|Y=c_k)=frac{sum_{i=1}^{N}{I(x_i^{(j)}=a_{jl}, y_i=c_k)}+lambda}{sum_{i=1}^{N}{I(y_i=c_k)+S_jlambda}}$$
- $lambda = 0$ 对应极大似然估计
- $lambda = 1$ 对应拉普拉斯平滑
- 朴素贝叶斯法实际上学习到生成数据的机制, 所以属于生成模型.
CH05 决策树
DT
- 决策树是一种基本的分类与回归方法
CH06 逻辑斯谛回归与最大熵模型
LR
- 逻辑斯谛回归是统计学中的经典分类方法
- 最大熵是概率模型学习的一个准则, 将其推广到分类问题得到最大熵模型
关于最大熵的学习,推荐阅读该章节的参考文献1,Berger, 1996, 有益于书中例子的理解以及最大熵原理的把握。
那么, 为什么LR和Maxent要放在一章?
-
都属于对数线性模型
-
都可用于二分类和多分类
-
两种模型的学习方法一般采用极大似然估计, 或正则化的极大似然估计. 可以形式化为无约束最优化问题, 求解方法有IIS, GD, BFGS等
-
在Logistic regression中有如下描述,
Logistic regression, despite its name, is a linear model for classification rather than regression. Logistic regression is also known in the literature as logit regression, maximum-entropy classification (MaxEnt) or the log-linear classifier. In this model, the probabilities describing the possible outcomes of a single trial are modeled using a logistic function.
还有这样的描述
Logistic regression is a special case of maximum entropy with two labels +1 and −1.
CH07 支持向量机
SVM
- 支持向量机是一种二分类模型.
- 基本模型是定义在特征空间上的间隔最大化的线性分类器, 间隔最大使他有别于感知机
CH08 提升方法
Boosting
- 提升方法是一种常用的统计学习方法, 应用广泛且有效.
————分割线————
姑且在这里分一下, 因为后面HMM和CRF通常会引出概率图模型的介绍, 在<机器学习,周志华>里面更是用了一个单独的概率图模型章节来包含HMM,MRF, CRF等内容. 另外从HMM到CRF本身也有很多相关的点.
CH09 EM算法及其推广
EM
-
EM算法是一种迭代算法, 用于含有隐变量的概率模型参数极大似然估计, 或者极大后验概率估计. (这里的极大似然估计和极大后验概率估计是学习策略)
-
如果概率模型的变量都是观测变量, 那么给定数据, 可以直接用极大似然估计法, 或贝叶斯估计法估计模型参数.
注意书上这个描述如果不理解,参考CH04中朴素贝叶斯法的参数估计部分。
-
这部分代码实现了BMM和GMM, 值得看下
-
关于EM, 这个章节写的不多, EM是十大算法之一, EM和Hinton关系紧密, Hinton在2018年ICLR上发表了Capsule Network的第二篇文章
CH10 隐马尔可夫模型
HMM
- 隐马尔可夫模型是可用于标注问题的统计学习模型, 描述由隐藏的马尔可夫链随机生成观测序列的过程, 属于生成模型.
- 隐马尔可夫模型是关于时序的概率模型, 描述由一个隐藏的马尔可夫链随机生成不可观测的状态的序列, 再由各个状态速记生成一个观测而产生观测的序列的过程.
- 可用于标注(Tagging)问题, 状态对应标记.
- 三个基本问题: 概率计算问题, 学习问题, 预测问题.
CH11 条件随机场
CRF
- 条件随机场是给定一组输入随机变量条件下另一组输出随机变量的条件概率分布模型, 其特点是假设输出随机变量构成马尔可夫随机场.
- 概率无向图模型, 又称为马尔可夫随机场, 是一个可以由无向图表示的联合概率分布.
- 三个基本问题: 概率计算问题, 学习问题, 预测问题
CH12 统计学习方法总结
Summary
这章就简单的几页, 可以考虑如下阅读套路
- 和第一章一起看
- 在前面的学习中遇到不清楚的问题的时候, 过一遍这个章节.
- 将这一章看厚, 从这一章展开到其他十个章节. 李老师这本书真的是每次刷都会有新的收获.
后记
整个这本书里面各章节也不是完全独立的, 这部分希望整理章节之间的联系以及适用的数据集. 算法到底实现到什么程度, 能跑什么数据集也是一房面.