RNN(Recurrent Neural Networks,循环神经网络)是一种具有短期记忆能力的神经网络模型,可以处理任意长度的序列,在自然语言处理中的应用非常广泛,比如机器翻译、文本生成、问答系统、文本分类等。
但由于梯度爆炸或梯度消失,RNN存在长期依赖问题,难以建立长距离的依赖关系,于是引入了门控机制来控制信息的累积速度,包括有选择地加入新信息,并有选择地遗忘之前积累的信息。比较经典的基于门控的RNN有LSTM(长短期记忆网络)和GRU(门控循环单元网络)。
有关RNN,LSTM和GRU的相关理论知识可以看我以前的笔记:《深度学习之循环神经网络(RNN)》 、《循环神经网络之LSTM和GRU》
这篇博客整理用TensorFlow构建RNN的内容,主要包括两方面,一是分别用RNN、LSTM和GRU作为记忆细胞,构建一个单向堆叠的循环神经网络,也就是有多个循环网络层(单向);二是构建双向RNN模型,这在自然语言处理中比较常见,比如Bi-LSTM+CRF做命名实体识别。
一、堆叠RNN、LSTM和GRU
1、堆叠RNN的结构和特性
RNN的一般性内容就不介绍了,如果不熟悉请看以上列出的笔记。我们先来看看堆叠RNN的结构。
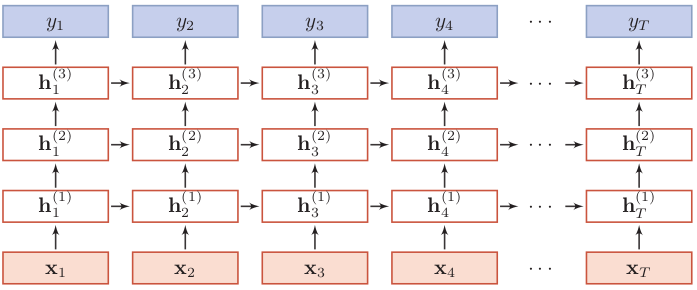
以上是按时间展开的堆叠循环神经网络。一般的,我们定义 ht(l)为在时刻 t 时第 l 层的隐状态,则它是由时刻t-1第l层的隐状态与时刻t第l-1层的隐状态共同决定:
![]()
其中U(l)、W(l)是权重矩阵,b(l)是偏置,ht(0) = xt 。
我们可以看到,如果一共有T步,那么会有T个输出:y1,y2,...,yT。但一般只取最后一个输出yT,相应的隐状态也取最后时刻最后一个循环层的隐状态,比如上面就是取hT(3),这是代码中需要注意的地方。
2、RNN、LSTM和GRU的区别
RNN、LSTM与GRU这三中循环神经网络结构,在构建时的区别有两个:
一是在t时刻,RNN最后一个循环层只有一个隐状态,就用这个隐状态来计算输出;LSTM在最后一个循环层有两个隐状态,一个是长期状态Ct,一个是短期状态ht,长期状态由Tanh函数激活,然后通过输出门过滤后得到短期状态,而用来输入到全连接层计算模型输出的是短期状态。于是在下图中可以看到,ht一方面往上传递去计算当前时刻的模型输出,另一方面顺时间传递去计算下一个隐状态ht-1
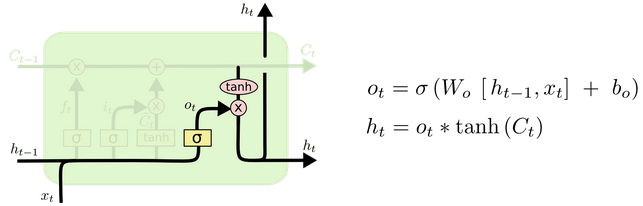
GRU在最后一个循环层也只有一个隐状态,因为没有引入额外的内部状态C,而直接在当前状态ht和历史状态ht-1之间引入线性依赖关系。从下图可以看到,隐状态ht由前一时刻的隐状态ht-1和候选状态决定。

二是在TensorFlow中,要指定RNN中记忆细胞的激活函数,一般为ReLU函数,而LSTM和GRU中的激活函数已经确定为Sigmoid函数和Tanh函数了。
3、LSTM的参数初始化
还有一点要说明,一般在深度网络参数学习时,参数初始化的值一般都比较小,在训练 LSTM 网络时,过小的参数值会使得遗忘门的值比较小。这意味着前一时刻的信息大部分都丢失了,这样网络很难捕捉到长距离的依赖信息。因此遗忘门的参数初始值一般都设得比较大,其偏置向量 bf 设为 1 或 2。而TensorFlow将bf初始化为1的向量。
![]()
4、TensorFlow核心代码
按照上一步所说的,RNN、LSTM和GRU的不同点在于隐状态和激活函数,这也体现在了TensorFlow的代码中。堆叠三个循环层,每层神经元的个数均为100,这三种记忆细胞的定义代码如下,构建的模型除了这部分不同以外,其他都是一样的。
def cell_selected(cell):
if cell == "RNN": # 指定激活函数为ReLU函数,然后构造三个RNN细胞状态 # 构建堆叠的RNN模型 # 每个时刻都有一个输出和一个隐状态(或多个隐状态),我们只取最后一个输出和隐状态 # 但是TensofFlow中不知道为啥取了最后时刻的三个隐状态,用于计算最终输出。 rnn_cells = [tf.nn.rnn_cell.BasicRNNCell(num_units=n_neurons,activation=tf.nn.relu) for layer in range(n_layers)] multi_layer_cell = tf.nn.rnn_cell.MultiRNNCell(rnn_cells) outputs, states = tf.nn.dynamic_rnn(multi_layer_cell, X, dtype=tf.float32) return tf.concat(axis=1, values=states) elif cell == "LSTM": # 构造三个LSTM记忆细胞,不用管激活函数 # states[-1]中包含了长期状态和短期状态,这里取最后一个循环层的短期状态 lstm_cells = [tf.nn.rnn_cell.LSTMCell(num_units=n_neurons) for layer in range(n_layers)] multi_cell = tf.nn.rnn_cell.MultiRNNCell(lstm_cells) outputs, states = tf.nn.dynamic_rnn(multi_cell, X, dtype=tf.float32) return states[-1][1] elif cell == "GRU": # GRU和LSTM大致相同,但是states[-1]中只包含了短期状态。 gru_cells = [tf.nn.rnn_cell.GRUCell(num_units=n_neurons) for layer in range(n_layers)] multi_cell = tf.nn.rnn_cell.MultiRNNCell(gru_cells) outputs, states = tf.nn.dynamic_rnn(multi_cell, X, dtype=tf.float32) return states[-1]
取记忆细胞的隐状态这一步需要好好理解。我们一一来看,这三个细胞状态在最后一时刻的隐状态和经过处理用来求模型输出的隐状态是什么样的。
(1)在RNN中,用tf.concat()来处理RNN记忆细胞的隐状态。未处理之前的states是三个tuple元素,是三个循环层最后一步的隐状态,维度是[batch-size, n_neurons],100是神经元的个数。
(<tf.Tensor 'rnn/rnn/while/Exit_3:0' shape=(?, 100) dtype=float32>, <tf.Tensor 'rnn/rnn/while/Exit_4:0' shape=(?, 100) dtype=float32>, <tf.Tensor 'rnn/rnn/while/Exit_5:0' shape=(?, 100) dtype=float32>)
用tf.cncat()按第1个维度拼接后如下。可见是将最后时刻三个循环层的隐状态的值拼接在了一起。这是TensorFlow在堆叠RNN中想要的格式,我不太明白,按道理只要取三个中的最后一个就可以了啊。
<tf.Tensor 'concat:0' shape=(?, 300) dtype=float32>
(2)在LSTM中,得到的states包含三个tuple元素,而每个tuple中又有两个元素,第一个是长期状态,第二个是短期状态。显然我们要取的是最后一层中的短期状态,用此用states[-1][1]取到。
(LSTMStateTuple(c=<tf.Tensor 'rnn/while/Exit_3:0' shape=(?, 100) dtype=float32>, h=<tf.Tensor 'rnn/while/Exit_4:0' shape=(?, 100) dtype=float32>), LSTMStateTuple(c=<tf.Tensor 'rnn/while/Exit_5:0' shape=(?, 100) dtype=float32>, h=<tf.Tensor 'rnn/while/Exit_6:0' shape=(?, 100) dtype=float32>), LSTMStateTuple(c=<tf.Tensor 'rnn/while/Exit_7:0' shape=(?, 100) dtype=float32>, h=<tf.Tensor 'rnn/while/Exit_8:0' shape=(?, 100) dtype=float32>))
(3)在GRU中,得到的states包含三个元素,就是最后一步隐状态的值,因此只要用states[-1]取到最后一层的隐状态即可。
(<tf.Tensor 'rnn/while/Exit_3:0' shape=(?, 100) dtype=float32>, <tf.Tensor 'rnn/while/Exit_4:0' shape=(?, 100) dtype=float32>, <tf.Tensor 'rnn/while/Exit_5:0' shape=(?, 100) dtype=float32>)
5、完整代码
为了方便在三种记忆细胞之间进行切换,我定义了以上选择记忆细胞的函数。基于MINIST数据集,构建了一个具有三个循环层的单向RNN网络,每个循环层的神经元个数为100,记忆细胞分别选择RNN、LSTM和GRU。
import tensorflow as tf import numpy as np import time from datetime import timedelta # 记录训练花费的时间 def get_time_dif(start_time): end_time = time.time() time_dif = end_time - start_time return timedelta(seconds=int(round(time_dif))) (X_train, y_train), (X_test, y_test) = tf.keras.datasets.mnist.load_data() # 这里和卷积神经网络那不同,RNN中的输入维度是(batch-size,28,28),而不是(batch-size,784) X_train = X_train.astype(np.float32)/ 255.0 X_test = X_test.astype(np.float32)/ 255.0 y_train = y_train.astype(np.int32) y_test = y_test.astype(np.int32) X_valid, X_train = X_train[:5000], X_train[5000:] y_valid, y_train = y_train[:5000], y_train[5000:] def shuffle_batch(X, y, batch_size): rnd_idx = np.random.permutation(len(X)) n_batches = len(X) // batch_size for batch_idx in np.array_split(rnd_idx, n_batches): X_batch, y_batch = X[batch_idx], y[batch_idx] yield X_batch, y_batch n_steps = 28 n_inputs = 28 n_neurons = 100 n_outputs = 10 n_layers = 3 learning_rate = 0.001 X = tf.placeholder(tf.float32, [None, n_steps, n_inputs]) y = tf.placeholder(tf.int32, [None]) # 选择记忆细胞 def cell_selected(cell): if cell == "RNN": # 指定激活函数为ReLU函数,然后构造三个RNN细胞状态 # 构建堆叠的RNN模型 # 每个时刻都有一个输出和一个隐状态(或多个隐状态),我们只取最后一个输出和隐状态 # 但是TensofFlow中不知道为啥取了最后时刻的三个隐状态,用于计算最终输出。 rnn_cells = [tf.nn.rnn_cell.BasicRNNCell(num_units=n_neurons,activation=tf.nn.relu) for layer in range(n_layers)] multi_layer_cell = tf.nn.rnn_cell.MultiRNNCell(rnn_cells) outputs, states = tf.nn.dynamic_rnn(multi_layer_cell, X, dtype=tf.float32) return tf.concat(axis=1, values=states) elif cell == "LSTM": # 构造三个LSTM记忆细胞,不用管激活函数 # states[-1]中包含了长期状态和短期状态,这里取最后一个循环层的短期状态 gru_cells = [tf.nn.rnn_cell.LSTMCell(num_units=n_neurons) for layer in range(n_layers)] multi_cell = tf.nn.rnn_cell.MultiRNNCell(gru_cells) outputs, states = tf.nn.dynamic_rnn(multi_cell, X, dtype=tf.float32) return states[-1][1] elif cell == "GRU": # GRU和LSTM大致相同,但是states[-1]中只包含了短期状态。 gru_cells = [tf.nn.rnn_cell.GRUCell(num_units=n_neurons) for layer in range(n_layers)] multi_cell = tf.nn.rnn_cell.MultiRNNCell(gru_cells) outputs, states = tf.nn.dynamic_rnn(multi_cell, X, dtype=tf.float32) return states[-1] def build_and_train(): # 调用上面定义的选择记忆细胞的函数,定义损失函数 logits = tf.layers.dense(cell_selected(cell), n_outputs, name="softmax") xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits) loss = tf.reduce_mean(xentropy, name="loss") optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate) training_op = optimizer.minimize(loss) correct = tf.nn.in_top_k(logits, y, 1) accuracy = tf.reduce_mean(tf.cast(correct, tf.float32)) init = tf.global_variables_initializer() saver = tf.train.Saver() n_epochs = 50 batch_size = 100 with tf.Session() as sess: init.run() start_time = time.time() # 记录总迭代步数,一个batch算一步 # 记录最好的验证精度 # 记录上一次验证结果提升时是第几步。 # 如果迭代2000步后结果还没有提升就中止训练。 total_batch = 0 best_acc_val = 0.0 last_improved = 0 require_improvement = 2000 flag = False for epoch in range(n_epochs): for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size): sess.run(training_op, feed_dict={X: X_batch, y: y_batch}) # 每次迭代10步就验证一次 # # 如果验证精度提升了,就替换为最好的结果,并保存模型 if total_batch % 10 == 0: acc_batch = accuracy.eval(feed_dict={X: X_batch, y: y_batch}) acc_val = accuracy.eval(feed_dict={X: X_valid, y: y_valid}) if acc_val > best_acc_val: best_acc_val = acc_val last_improved = total_batch save_path = saver.save(sess, "./my_model_Cell_Selected.ckpt") improved_str = 'improved!' else: improved_str = '' time_dif = get_time_dif(start_time) msg = 'Epoch:{0:>4}, Iter: {1:>6}, Acc_Train: {2:>7.2%}, Acc_Val: {3:>7.2%}, Time: {4} {5}' print(msg.format(epoch, total_batch, acc_batch, acc_val, time_dif, improved_str)) # 记录总迭代步数 total_batch += 1 # 如果2000步以后还没提升,就中止训练。 if total_batch - last_improved > require_improvement: print("Early stopping in ",total_batch," step! And the best validation accuracy is ",best_acc_val, '.') flag = True break if flag: break with tf.Session() as sess: saver.restore(sess, "./my_model_Cell_Selected.ckpt") acc_test= accuracy.eval(feed_dict={X: X_test, y: y_test}) print(" Test_accuracy:{0:>7.2%}".format(acc_test)) if __name__ == "__main__": cell = "LSTM" # RNN/LSTM/GRU,在这里选择记忆细胞 build_and_train()
分别选择记忆细胞为RNN、LSTM和GRU,得到的结果为:
RNN 耗时3分3秒 最好验证精度98.72% 测试精度98.41% LSTM 耗时6分35秒 最好验证精度99.22% 测试精度98.81% GRU 耗时6分9秒 最好验证精度99.26% 测试精度98.97%
二、双向LSTM模型
1、双向LSTM的结构
双向LSTM(Bidirectional Long-Short Term Memorry,Bi-LSTM)不仅能利用到过去的信息,还能捕捉到后续的信息,比如在词性标注问题中,一个词的词性由上下文的词所决定,那么用双向LSTM就可以利用好上下文的信息。
双向LSTM由两个信息传递相反的LSTM循环层构成,其中第一层按时间顺序传递信息,第二层按时间逆序传递信息。
没有去找双向LSTM的图了,就看这个双向RNN的结构来学习吧,理解了双向RNN,那么把循环层的记忆细胞换成LSTM就行。
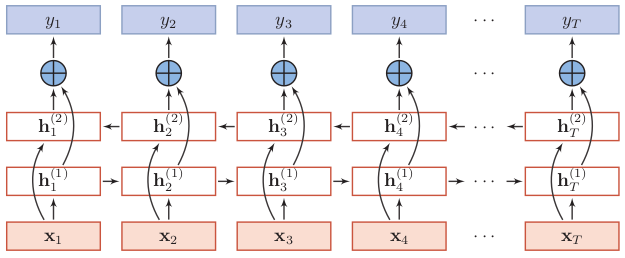
2、双向LSTM隐状态的计算
关键在于隐状态如何计算。为了简单,还是按照双向RNN的公式进行理解,我们看隐状态如何计算。可以看到t时刻第一层(顺时间循环层)的隐状态ht(1)取决于前一时刻的隐状态ht-1(1)和输入值xt,这一点非常容易理解。
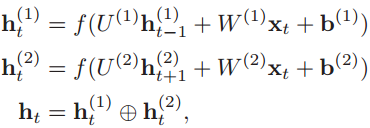
而要注意的是第二层(逆时间循环层)的隐状态则依然取决于前一时刻的隐状态和输入值x,这与堆叠的LSTM不同,堆叠的LSTM其l层的隐状态不由输入值x直接输入得到,而是取决于该层前一时刻的隐状态和当前时刻下一层的隐状态。如下的公式就是堆叠的循环网络层中隐状态的计算过程。
![]()
双向LSTM和堆叠的LSTM可以结合使用,在顺时间循环层我们可以构造堆叠多层的LSTM,同样,在逆时间循环层可以堆叠多个。
而双向LSTM的一个循环层中有两个隐状态,长期状态C用于内部传递信息,不抛头露面,而短期状态h则作为该循环层的输出,用于其他循环层或全连接层的计算。因此在对得的双向LSTM的最后一步,会有超过4个隐状态存在。
这次构建的双向LSTM模型,在顺时间循环层和逆时间循环层都分别堆叠了两层LSTM,每层神经元个数都为100,因此循环网络层总共有4层,最后一步的隐状态有8个。
def bi_lstm(): # 顺时间循环层的记忆细胞,堆叠了两层 lstm_fw1 = tf.nn.rnn_cell.LSTMCell(num_units=n_neurons) lstm_fw2 = tf.nn.rnn_cell.LSTMCell(num_units=n_neurons) lstm_forward = tf.nn.rnn_cell.MultiRNNCell(cells=[lstm_fw1,lstm_fw2]) # 逆时间循环层的记忆细胞,堆叠了两层 lstm_bc1 = tf.nn.rnn_cell.LSTMCell(num_units=n_neurons) lstm_bc2 = tf.nn.rnn_cell.LSTMCell(num_units=n_neurons) lstm_backward = tf.nn.rnn_cell.MultiRNNCell(cells=[lstm_bc1,lstm_bc2]) # 计算输出和隐状态 outputs,states=tf.nn.bidirectional_dynamic_rnn(cell_fw=lstm_forward, cell_bw=lstm_backward,inputs=X,dtype=tf.float32) # 取到顺时间循环层和拟时间循环层的最后一个隐状态 state_forward = states[0][-1][-1] state_backward = states[1][-1][-1] # 把两个隐状态拼接起来。 return state_forward+state_backward
下面是隐状态states的情况,第一个元素是顺时间循环层的隐状态,其中短期状态有两个,我们选择最后一个堆叠层的短期状态:states[0][-1][-1]。同理,第二个元素是逆时间循环层的隐状态,我们用states[1][-1][-1]来取到最后一个堆叠层的短期状态。
((LSTMStateTuple(c=<tf.Tensor 'bidirectional_rnn/fw/fw/while/Exit_3:0' shape=(?, 100) dtype=float32>, h=<tf.Tensor 'bidirectional_rnn/fw/fw/while/Exit_4:0' shape=(?, 100) dtype=float32>), LSTMStateTuple(c=<tf.Tensor 'bidirectional_rnn/fw/fw/while/Exit_5:0' shape=(?, 100) dtype=float32>, h=<tf.Tensor 'bidirectional_rnn/fw/fw/while/Exit_6:0' shape=(?, 100) dtype=float32>)), (LSTMStateTuple(c=<tf.Tensor 'bidirectional_rnn/bw/bw/while/Exit_3:0' shape=(?, 100) dtype=float32>, h=<tf.Tensor 'bidirectional_rnn/bw/bw/while/Exit_4:0' shape=(?, 100) dtype=float32>), LSTMStateTuple(c=<tf.Tensor 'bidirectional_rnn/bw/bw/while/Exit_5:0' shape=(?, 100) dtype=float32>, h=<tf.Tensor 'bidirectional_rnn/bw/bw/while/Exit_6:0' shape=(?, 100) dtype=float32>)))
取到两个循环层的两个短期状态之后,通过简单的拼接,就可以输入到全连接层了,即states[0][-1][-1]+states[1][-1][-1]。
3、完整代码
对MINIST数据集构建双向LSTM分类器,训练耗时12分38秒,最佳验证精度为99.16%,测试精度为98.83%
#-*- coding: utf-8 -*- from __future__ import division, print_function, unicode_literals import tensorflow as tf import numpy as np import time from datetime import timedelta # 记录训练花费的时间 def get_time_dif(start_time): end_time = time.time() time_dif = end_time - start_time return timedelta(seconds=int(round(time_dif))) (X_train, y_train), (X_test, y_test) = tf.keras.datasets.mnist.load_data() # 这里和卷积神经网络那不同,RNN中的输入维度是(batch-size,28,28),而不是(batch-size,784) X_train = X_train.astype(np.float32)/ 255.0 X_test = X_test.astype(np.float32)/ 255.0 y_train = y_train.astype(np.int32) y_test = y_test.astype(np.int32) X_valid, X_train = X_train[:5000], X_train[5000:] y_valid, y_train = y_train[:5000], y_train[5000:] def shuffle_batch(X, y, batch_size): rnd_idx = np.random.permutation(len(X)) n_batches = len(X) // batch_size for batch_idx in np.array_split(rnd_idx, n_batches): X_batch, y_batch = X[batch_idx], y[batch_idx] yield X_batch, y_batch n_steps = 28 n_inputs = 28 n_neurons = 100 n_outputs = 10 learning_rate = 0.001 X = tf.placeholder(tf.float32, [None, n_steps, n_inputs]) y = tf.placeholder(tf.int32, [None]) def bi_lstm(): # 顺时间循环层的记忆细胞,堆叠了两层 lstm_fw1 = tf.nn.rnn_cell.LSTMCell(num_units=n_neurons) lstm_fw2 = tf.nn.rnn_cell.LSTMCell(num_units=n_neurons) lstm_forward = tf.nn.rnn_cell.MultiRNNCell(cells=[lstm_fw1,lstm_fw2]) # 拟时间循环层的记忆细胞,堆叠了两层 lstm_bc1 = tf.nn.rnn_cell.LSTMCell(num_units=n_neurons) lstm_bc2 = tf.nn.rnn_cell.LSTMCell(num_units=n_neurons) lstm_backward = tf.nn.rnn_cell.MultiRNNCell(cells=[lstm_bc1,lstm_bc2]) # 计算输出和隐状态 outputs,states=tf.nn.bidirectional_dynamic_rnn(cell_fw=lstm_forward, cell_bw=lstm_backward,inputs=X,dtype=tf.float32) # 取到顺时间循环层和拟时间循环层的最后一个隐状态 state_forward = states[0][-1][-1] state_backward = states[1][-1][-1] # 把两个隐状态拼接起来。 return state_forward+state_backward def build_and_train(): # 调用上面的定义双向LSTM的函数,定义损失函数 logits = tf.layers.dense(bi_lstm(), n_outputs, name="softmax") xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits) loss = tf.reduce_mean(xentropy, name="loss") optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate) training_op = optimizer.minimize(loss) correct = tf.nn.in_top_k(logits, y, 1) accuracy = tf.reduce_mean(tf.cast(correct, tf.float32)) init = tf.global_variables_initializer() saver = tf.train.Saver() n_epochs = 50 batch_size = 100 with tf.Session() as sess: init.run() start_time = time.time() # 记录总迭代步数,一个batch算一步 # 记录最好的验证精度 # 记录上一次验证结果提升时是第几步。 # 如果迭代2000步后结果还没有提升就中止训练。 total_batch = 0 best_acc_val = 0.0 last_improved = 0 require_improvement = 2000 flag = False for epoch in range(n_epochs): for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size): sess.run(training_op, feed_dict={X: X_batch, y: y_batch}) # 每次迭代10步就验证一次 # # 如果验证精度提升了,就替换为最好的结果,并保存模型 if total_batch % 10 == 0: acc_batch = accuracy.eval(feed_dict={X: X_batch, y: y_batch}) acc_val = accuracy.eval(feed_dict={X: X_valid, y: y_valid}) if acc_val > best_acc_val: best_acc_val = acc_val last_improved = total_batch save_path = saver.save(sess, "./my_model_Bi_LSTM.ckpt") improved_str = 'improved!' else: improved_str = '' time_dif = get_time_dif(start_time) msg = 'Epoch:{0:>4}, Iter: {1:>6}, Acc_Train: {2:>7.2%}, Acc_Val: {3:>7.2%}, Time: {4} {5}' print(msg.format(epoch, total_batch, acc_batch, acc_val, time_dif, improved_str)) # 记录总迭代步数 total_batch += 1 # 如果2000步以后还没提升,就中止训练。 if total_batch - last_improved > require_improvement: print("Early stopping in ",total_batch," step! And the best validation accuracy is ",best_acc_val, '.') flag = True break if flag: break with tf.Session() as sess: saver.restore(sess, "./my_model_Bi_LSTM.ckpt") acc_test= accuracy.eval(feed_dict={X: X_test, y: y_test}) print(" Test_accuracy:{0:>7.2%}".format(acc_test)) if __name__ == "__main__": build_and_train()
参考资料:
1、《Hands on Machine Learning with Scikit-Learn and TensorFlow》
2、https://blog.csdn.net/luoganttcc/article/details/83384823