标题名字乱取的,吐槽一下《初等数论初步》的命名。
1 网络流的概念
1.1 引入
“分配”是生产生活中一类常见的问题。如何分配才最好,是一个有技术含量的问题。
对于“分配最优”的问题,动态规划是一种有效的解决方法。但是,有些分配无法描述出一个准确的“决策”“状态”“阶段”轮廓。我们来看下面这样一个简单的问题:
一个研究性学习小组收到了一个含有25个任务的课题,组内一共有甲,乙,丙,丁,戊五个同学。他们工作的效率和工作的态度(最多愿意做多少任务)各不相同,具体如下:
姓名 任务数上限 单个任务耗时 甲 4 42min 乙 5 56min 丙 6 71min 丁 7 108min 戊 8 121min
假设任务不能同时做,求完成所有任务所需的最小时间。
这个问题似乎不太好用动态规划。以前(i)个人的顺序划分阶段?似乎不太合适。这里人与人之间的关联似乎不大。
这个问题可以用多维的线性规划来做,也可以考虑用网络流来解决。这是图论中一个重要的算法。
为方便描述,现选定一个组长。我们来看这个简单的流程图:
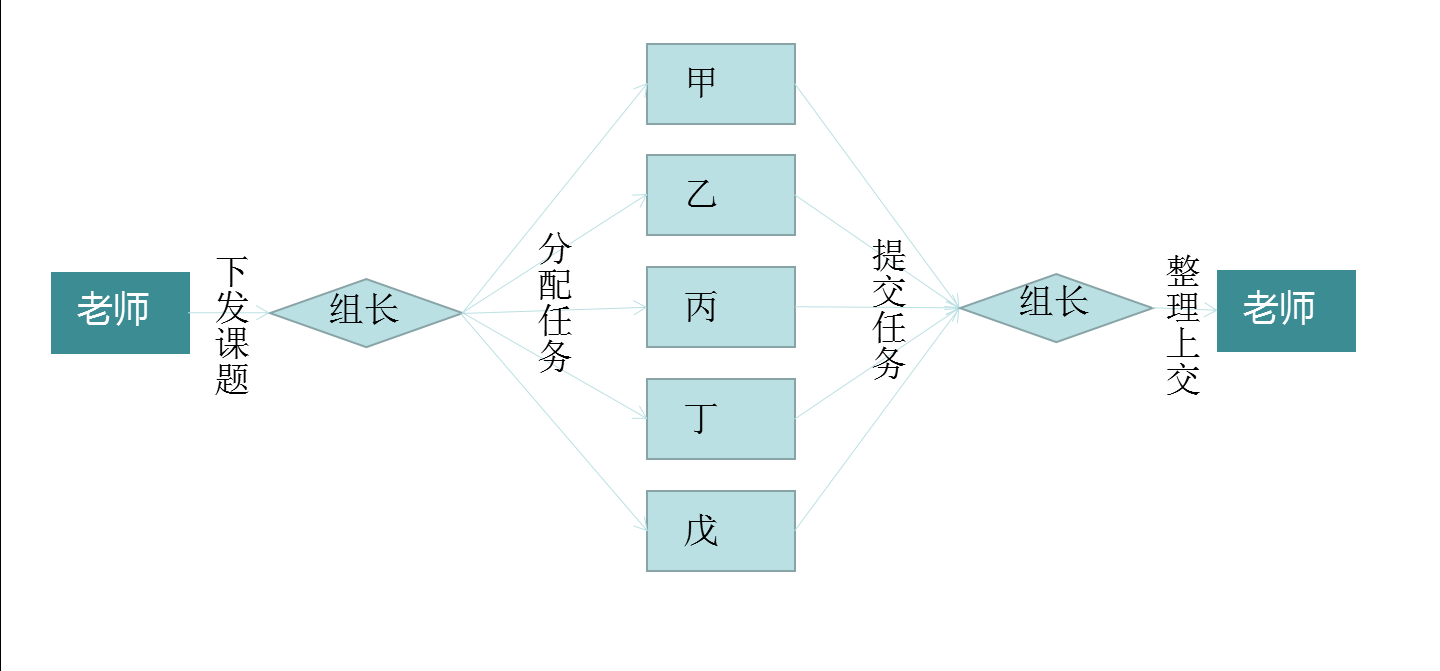
这个流程图就像一个一个生产线,25个任务从老师那里出来,最后又回到老师那里去了。当然,回去的是完成的任务。
可以对任务作出如下分配:
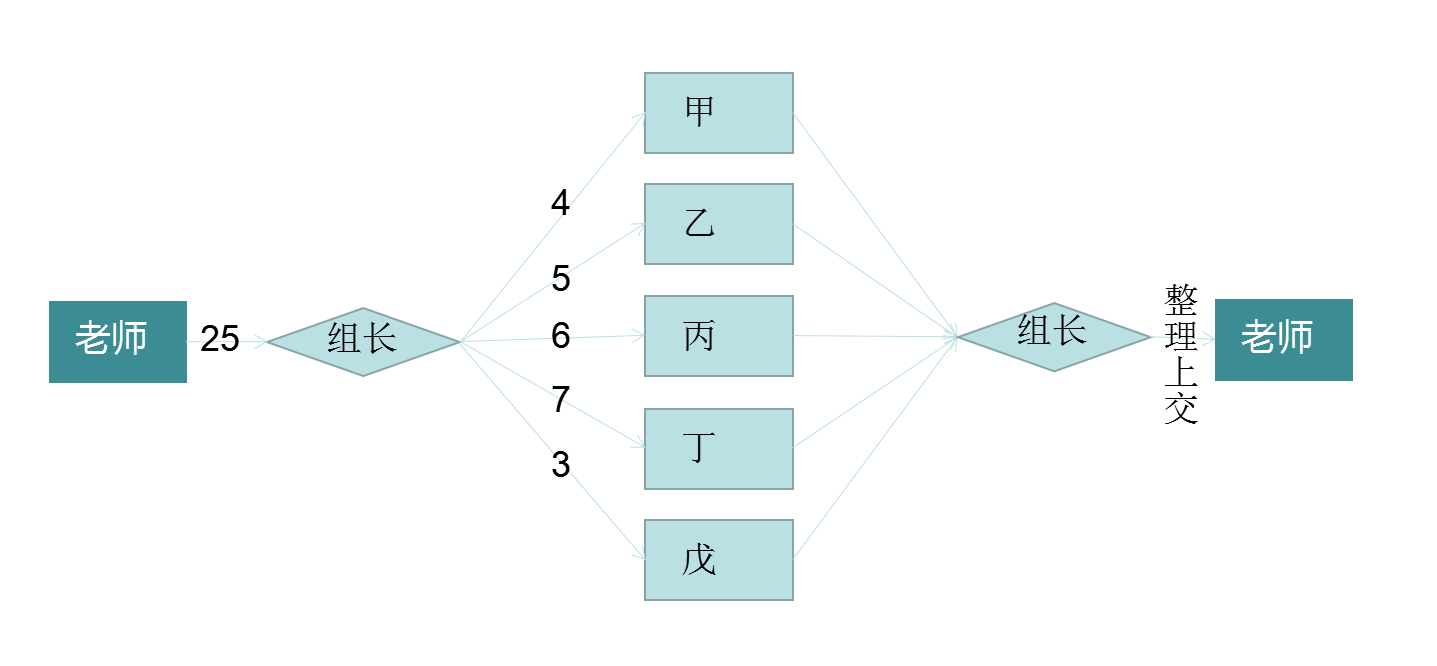
如图,每一个箭头上都标上了每个人分配的任务,总共耗时33小时13分钟。
可以看到,如果把每个人看成一个节点,那么人只负责“加工”任务,不会“储存”任务。这是一个非常重要的特征。更进一步的,我们可以提炼出其中的数学模型。
1.2 定义
一个网络(G)是一个有向图,其每一条边((x,y))可以用一个非负数(c(x,y))表示这条边的“容量”(capacity)。规定如果((x,y))不是这个图中的边,则(c(x,y)=0)。有些时候,网络中的边又叫做弧。
每一个这样的网络中都有两个特殊的节点:源点(S)和汇点(T)。
设函数(f(u,v))是作用在边((u,v))上的函数,满足:
1.(f(u,v) leq c(u,v))
2.(f(u,v) = -f(v,u))
3.(forall x
eq S, x
eq T, sum f(u,x) = sum f(x,v))
那么称(f)是网络(G)的一个流函数。对于一个边((u,v)),(f(u,v))就是它的流量。
以上这三个性质分别称为容量限制,斜对称,流量守恒。请结合“水流”和“河道”的关系加强理解:水流不会超过河道,且不可压缩。
容量限制还有非常棒的一点:它省去了我写(sum)下标的麻烦,因为不在边上的流量一定是(0)。(当然,这样做未必标准规范。)
在上面的任务分配中,从“组长”到“甲”的流量为(4),从“组长”到“乙”的流量为(5),以此类推。
源点(S)和汇点(T)比较特殊,它们可以“发送”和“储存”流量。源点向整个网络运输的流量就是整个网络的流量,大小为(sum f(S,v))。
网络流还有一个有趣的性质:选取一个不含源点、汇点的点集,这个点集也满足流量平衡!这个性质可以看做是高斯定理的“离散版本”,在之后的网络流建模中会有所体现。
网络流的思想非常巧妙;正因如此,用网络流解题不像其他数据结构,是需要花费一点心思的。如何构建网络?如何转换问题?这些都是需要考虑的。
2 有关算法
2.1 最大流算法
网络中的最大流量就叫最大流。一个网络的流函数有很多;但幸运的是,我们可以避免直接对流函数操作,采用一种巧妙的方法。
2.1.1 Edmonds-Karp增广路算法
我们关注源点发送的其中一股流量。这股流量通过一条路径,最终流向了汇点。这样的路径叫做增广路。不难想到,路上的流量(f)等于路上容量的最小值(min c)。
仔细一想,是不是源点发送的流量都会经过若干条增广路,然后全部流向汇点?我们只要尽可能地找出增广路,就可以求出最大流了!
这就是Edmonds-Karp算法的雏形了。通过BFS,我们可以找到一条增广路,并求出这条路上的流量。如何再找出一条增广路呢?再做一次BFS会返回同样的路径,而直接维护边上的信息又不太方便。
我们考虑直接修改增广路上的容量:求出流量(f)后,对路上的每一条边((x,y)),都执行(c(x,y)=c(x,y)-f),防止新的增广路超过容量。请注意,在原来流量(f)的基础上,我们还可能构造一个“逆流”(f'),使得某个(f(x,y))直接与(f'(x,y))抵消了。这样做是可行的,需要考虑。
通过执行(c(x,y)-=f),(c(y,x)+=f)后,得到的新网络叫做残量网络。在这个网络上添加的流量,一定不会超过原来的容量。
综上,通过BFS探测+构造残量网络的形式,我们可以分别求得若干个可行的流量(f,f',f'',cdots);相加就得到了整个网络的最大流。
首先是搜索增广路的部分:
inline bool find_argumenting_path()
{
memset(visit, 0, sizeof(visit));//标记
queue<int> q; q.push(S); inq[S] = Inf; visit[S] = true;
while(!q.empty())
{
int cur = q.front(); q.pop();
for(rg int e = head[cur]; e; e = edge[e].next)
{
if(edge[e].capacity <= 0)
continue;
int to = edge[e].to;
if(visit[to] == true)
continue;
inq[to] = min(inq[cur], edge[e].capacity);
pre_edge[to] = e;//标记边,方便记录路径
q.push(to); visit[to] = true;
if(to == T)
return true;
}
}
return false;
}
注意到这里我们用到了一个inq数组,它表示“某个节点的剩余流量”。可以这样理解:我们在源点处注入足够多的水,当水沿着边流动时,其一定要收到边容量的限制。最终到达汇点的水量就是我们本次需要增加的流量。因此,对于边((x,y)),一定有inq[y]=min(inq[x], edge[e].capacity)。
一旦找到了增广路,我们就将本次流量加入到答案中,并更新残量网络:
inline void update()
{
int cur = T;
while(cur != S)
{
int e = pre_edge[cur];
edge[e].capacity -= inq[T];
edge[e^1].capacity += inq[T];
cur = edge[e].front;
}
max_flow += inq[T];
}
根据之前的pre标记,我们可以还原一条从T到S的路径,并调整路径上的边的容量。
最后在主程序中代码如下:
while(find_argumenting_path() == true)
update();