棋盘游戏
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 3328 Accepted Submission(s): 1965
Problem Description
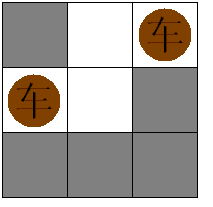
小希和Gardon在玩一个游戏:对一个N*M的棋盘,在格子里放尽量多的一些国际象棋里面的“车”,并且使得他们不能互相攻击,这当然很简单,但是Gardon限制了只有某些格子才可以放,小希还是很轻松的解决了这个问题(见下图)注意不能放车的地方不影响车的互相攻击。
所以现在Gardon想让小希来解决一个更难的问题,在保证尽量多的“车”的前提下,棋盘里有些格子是可以避开的,也就是说,不在这些格子上放车,也可以保证尽量多的“车”被放下。但是某些格子若不放子,就无法保证放尽量多的“车”,这样的格子被称做重要点。Gardon想让小希算出有多少个这样的重要点,你能解决这个问题么?
所以现在Gardon想让小希来解决一个更难的问题,在保证尽量多的“车”的前提下,棋盘里有些格子是可以避开的,也就是说,不在这些格子上放车,也可以保证尽量多的“车”被放下。但是某些格子若不放子,就无法保证放尽量多的“车”,这样的格子被称做重要点。Gardon想让小希算出有多少个这样的重要点,你能解决这个问题么?

Input
输入包含多组数据,
第一行有三个数N、M、K(1<N,M<=100 1<K<=N*M),表示了棋盘的高、宽,以及可以放“车”的格子数目。接下来的K行描述了所有格子的信息:每行两个数X和Y,表示了这个格子在棋盘中的位置。
第一行有三个数N、M、K(1<N,M<=100 1<K<=N*M),表示了棋盘的高、宽,以及可以放“车”的格子数目。接下来的K行描述了所有格子的信息:每行两个数X和Y,表示了这个格子在棋盘中的位置。
Output
对输入的每组数据,按照如下格式输出:
Board T have C important blanks for L chessmen.
Board T have C important blanks for L chessmen.
Sample Input
3 3 4
1 2
1 3
2 1
2 2
3 3 4
1 2
1 3
2 1
3 2
Sample Output
Board 1 have 0 important blanks for 2 chessmen.
Board 2 have 3 important blanks for 3 chessmen.
Author
Gardon
Source
建好图后,边数总共k条,枚举当前最大匹配中的边删除求最大匹配数是否减少。复杂度是O(n*n*k)=10^8

/* ID: LinKArftc PROG: 1281.cpp LANG: C++ */ #include <map> #include <set> #include <cmath> #include <stack> #include <queue> #include <vector> #include <cstdio> #include <string> #include <utility> #include <cstdlib> #include <cstring> #include <iostream> #include <algorithm> using namespace std; #define eps 1e-8 #define randin srand((unsigned int)time(NULL)) #define input freopen("input.txt","r",stdin) #define debug(s) cout << "s = " << s << endl; #define outstars cout << "*************" << endl; const double PI = acos(-1.0); const double e = exp(1.0); const int inf = 0x3f3f3f3f; const int INF = 0x7fffffff; typedef long long ll; const int maxn = 110; int uN, vN, k; int linker[maxn]; bool vis[maxn]; int mp[maxn][maxn]; bool dfs(int u) { for (int i = 1; i <= vN; i ++) { if (!vis[i] && mp[u][i]) { vis[i] = true; if (linker[i] == -1 || dfs(linker[i])) { linker[i] = u; return true; } } } return false; } int hungry() { memset(linker, -1, sizeof(linker)); int ret = 0; for (int i = 1; i <= uN; i ++) { memset(vis, 0, sizeof(vis)); if (dfs(i)) ret ++; } return ret; } int tmp[maxn]; int main() { //input; int u, v; int _t = 1; while (~scanf("%d %d %d", &uN, &vN, &k)) { memset(mp, 0, sizeof(mp)); for (int i = 1; i <= k; i ++) { scanf("%d %d", &u, &v); mp[u][v] = 1; } int ans = hungry(); for (int i = 1; i <= vN; i ++) tmp[i] = linker[i]; int cnt = 0; for (int i = 1; i <= vN; i ++) { int u = tmp[i]; if (u == -1) continue; mp[u][i] = 0; if (ans > hungry()) cnt ++; mp[u][i] = 1; } printf("Board %d have %d important blanks for %d chessmen. ", _t ++, cnt, ans); } return 0; }
找到最大匹配后,假设(x->y)是最大匹配中的一条,我们先删除这条边,使y失联,并将原图中(x->y)这条边删掉,再为x找增广路,如果能找到则说明(x->y)不是必须边,但是由于每次找增广路后都要还原原图,所以复杂度并不会降低。
