串
串的定义
串,即字符串(String)是由两个或多个字符组成的有序序列。一般记为 (S='a_1a_2cdot cdot cdot a_n')
其中,S是串名,单引号括起来的字符序列是串的值;(a_i)可以是字符、数字或其他字符;
串中字符的个数n称为串的长度。(n=0)时的串称为空串(用(varnothing)表示)
子串:串中任意个连续的字符组成的子序列
主串:包含子串的串
字符在主串的位置:字符在串中的序号
子串在主串的位置:子串的第一个字符在主串的位置
串是一种特殊的线性表,数据对象限定为字符集。基本操作以子串为操作对象
串的存储结构
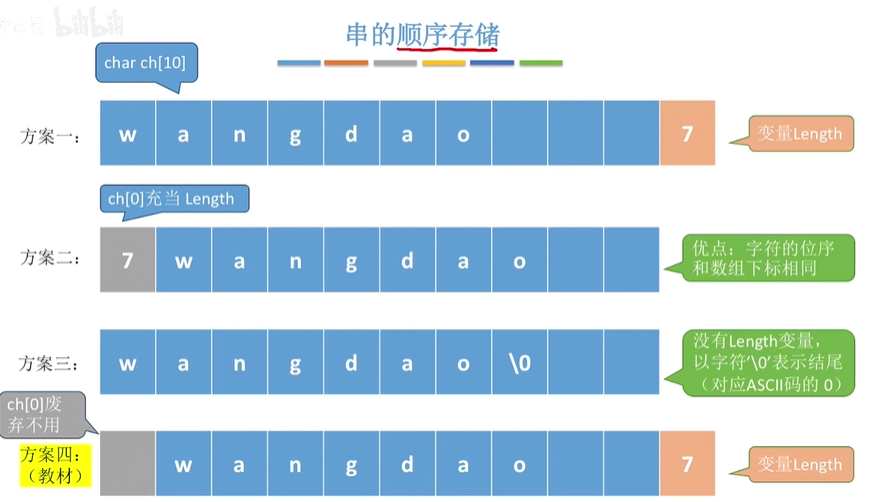
定长顺序存储表示
//定长数组
#define MAXLEN 255 //预定义最大串长为255
typedef struct{
char ch[MAXLEN]; //每个分量存储一个字符
int length; //串的实际长度
}SString;
堆分配存储表示
//动态分配
typedef struct{
char ch*; //按串长分配存储区,ch指向串的基地址
int length; //串的长度
}HString;
块链存储表示
typedef struct StringNode{
char ch; //每个结点存一个字符
struct StringNode* next;
}StringNode,*String;
//比较推荐
typedef struct StringNode{
char ch[4]; //每个结点存多个字符
struct StringNode* next;
}String;
串的基本操作
StrAssign(&T,chars); //赋值操作,把串T赋值为chars
StrCopy(&T,S); //复制操作,由串S复制得到串T
StrEmpty(S); //判空操作,若S为空串,则返回TRUE,否则返回FALSE
StrLength(S); //求串长,返回串S的元素个数
ClearString(&S); //清空操作,将S清为空串
DestoryString(&S); //销毁串。将串S销毁(回收存储空间)
Concat(&T,S1,S2); //串联接。用T返回由S1和S2联接而成的新串
SubString(&Sub,S,pos,len); //求子串。用Sub返回串S的第pos个字符起长度为len的子串
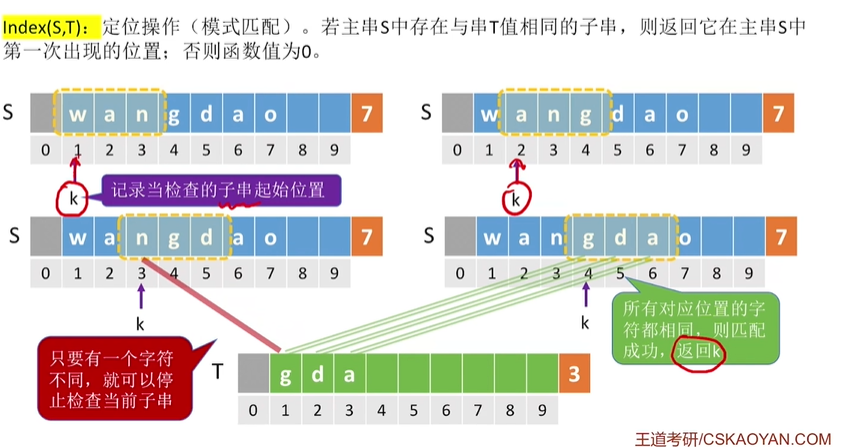
Index(S,T); //定位操作。若主串S存在与串T值相同的子串,则返回他在主串S第 //一次出现的位置
StrCompare(S,T); //比较操作。若S>T,则返回值>0;若S=T,则返回值=0;
//若S<T,则返回值<0
//从第一个字符开始往后依次对比,先出现更大字符的串就更大
//长串的前缀与短串相同时,长串更大
求子串
bool SubString(SSting &Sub,SSting S,int pos,int len)
{
//子串范围越界
if(pos+len-1>S.length)
return false;
for(int i=pos;i<pos+len;i++)
Sub.ch[i-pos+1]=S.ch[i];
Sub.length=len;
return false;
}
比较操作
int StrCompare(SSting S,SSting T)
{
for(int i=1;i<=S.length&&i<=T.length;i++)
{
if(S.ch[i]!=T.ch[i])
return S.ch[i]-T.ch[i];
}
//扫描过的所有字符都相同,则长度长的串更大
return S.length-T.length;
}
定位操作
int Index(SString S,SSting T)
{
int i=1,n=StrLength(S),m=StrLength(T);
SString sub;
while(i<=n-m+1)
{
SubString(sub,s,i,m);
if(StrCompare(sub,T)!=0)
++i;
else
return i; //返回子串在主串中的位置
}
return 0; //S中不存在与T相等的子串
}
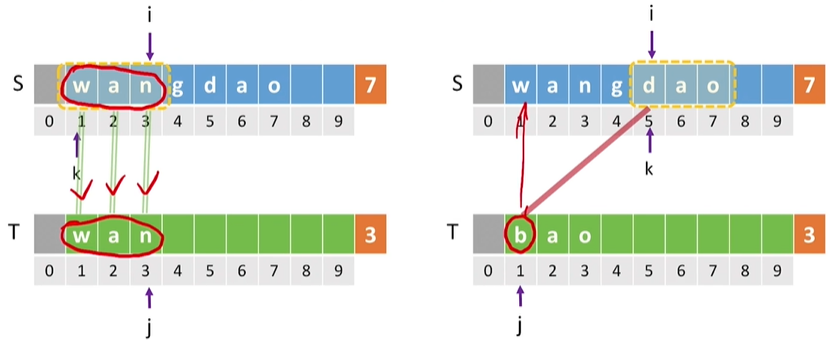
模式匹配算法
串的模式匹配:在主串中找到与模式串相同的子串,并返回其所在位置。
朴素模式匹配算法
int Index(SStromh S,SString T)
{
int i=1,j=1;
while(i<=S.length&&j<=T.length)
{
if(S.ch[i]==T.ch[i])
{
++i;++j;
}
else
{
i=i-j+2;
j=1; //指针后退重新开始匹配
}
}
if(j>T.length)
return i-T.length;
else
return 0;
}
性能分析
较好情况:每个子串第一个字符就与模式串不匹配
若模式串长度为m,主串长度为n,则
匹配成功的最好时间复杂度:(O(m))
匹配失败的最好时间复杂度:(O(n-m+1)=O(n-m)=O(n))
较坏情况:
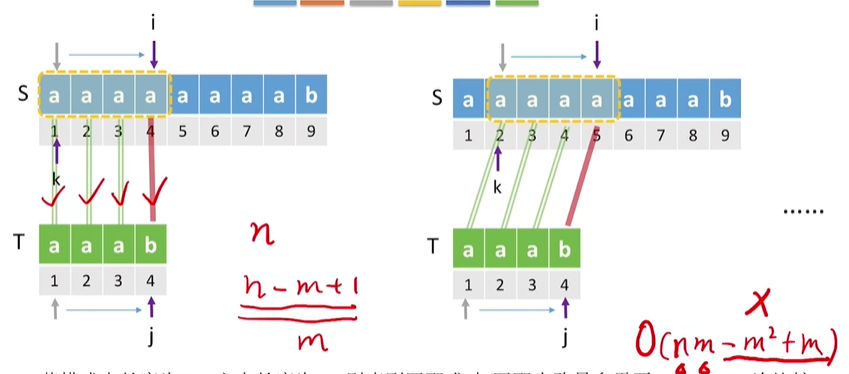
若模式串长度为m,主串长度为n,则直到匹配成功/匹配失败最多需要((n-m+1)*m)次比较
最坏时间复杂度:(O(nm))
KMP算法
朴素模式匹配算法的缺点:当某些子串与模式串部分匹配时,主串的扫描指针(i)经常回溯,导致时间开销增加。
改进思路:主串指针不回溯,只有模式串指针回溯。
如果(j=k)时才发现匹配识别,说明(1到k-1)都匹配成功

int Index_KMP(SString s,SString T,int next[])
{
int i=1;j=1;
while(i<=S.length&&j<=T.length)
{
if(j==0||S.ch[i]==T.ch[j])
{
++i;
++j; //继续比较后继字符
}
else
{
j=next[j];
}
}
if(j>T.length)
return i-T.length;
else
return 0;
}
next数组:当模式串的第(j)个字符匹配失败时,令模式串跳到(next[j])再继续匹配
串的前缀:包含第一个字符,且不包含最后一个字符的子串
串的后缀:包含最后一个字符,且不包含第一个字符的子串
当第(j)个字符匹配失败,由前(1到j-1)个字符组成的串记为(S),则:(next[j]=s)的最长相等前后缀长度+1
特别的,(next[1]=0)

//求next数组
void get_next(SString T,int next[])
{
int i=1,j=0;
next[1]=0;
while(i<T.length)
{
if(j==0||T.ch[i]==T.ch[j])
{
++i;++j;
//若pi=pj,则next[j+1]=next[j]+1;
next[i]=j;
}
else
{
//否则令j=next[j],循环继续
j=next[j];
}
}
}
KMP算法性能分析:当子串和模式串不匹配时,主串指针i不回溯,模式串指针(j=next[j])算法平均时间复杂度:(O(m+n))
KMP算法优化

当子串和模式串不匹配时(j=nextval[j])(减少对比)
//计算next数组修正值
void get_nextval(SString T,int nextval[])
{
int i=1,j=0;
nextval[1]=0;
while(i<T.length)
{
if(j==0||T.ch[i]==T.ch[j])
{
++i;++j;
if(T.ch[i]!=T.ch[j])
{
nextval[i]=j;
}
else
{
nextval[i]=nextval[j];
}
}
else
{
j=nextval[j];
}
}
}