Unity3D_向量（Vector3）数学基础

来源：https://blog.csdn.net/bobo553443/article/details/79481881

向量（Vector3）

在虚拟的游戏世界中，3D数学决定了游戏，如何计算和模拟出开发者以及玩家看到的每一帧画面。学习基础的3D数学知识可以帮主用户对游戏引擎产生更深刻的了解。 
向量定义：既有大小又有方向的量叫做向量。在空间中，向量用一段有方向的线段来表示。应用十分广泛，可用于描述具有大小和方向两个属性的物理量，例如物体运动的速度、加速度、摄像机观察方向、刚体受到的力等都是向量。因此向量是物理、动画、三维图形的基础。 
与向量相对的量成为标量:即只有大小没有方向的量。例如物体移动中的平均速率、路程。 
模：向量的长度标准化（Normalizing）：保持方向不变，将向量的长度变为1. 
单位向量：长度为1的向量。 
零向量：各分量均为0的向量 
向量运算——加减：向量的加法（减法）为各个分量分别相加（相减）。在物理上可以用来计算两个里的合力，或者几个速度份量的叠加。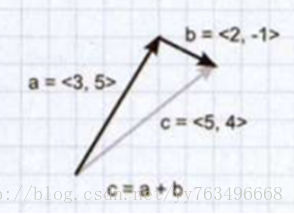 
 
向量运算——数乘：向量与一个标量相乘称为数乘。数乘可以对向量的长度进行缩放，如果标量大于0，那么向量的方向不变，若标量小于0，则向量的方向会变为反方向。 
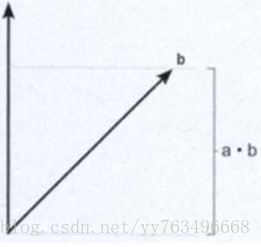
向量运算——点乘：两个向量点乘得到一个标量，数值等于两个向量长度相乘再乘以两者夹角的余弦值。如果两个向量a,b均为单位向量，那么a.b等于向量b在向量a方向上的投影的长度（或者说向量a在向量b方向上的投影）。 

把词语拆成字逐个分析。
“弦”代表长，也就是斜边，从“勾三股四弦五”中迁移过来。
“正”就是正对，表示直角三角形中角的对边。
“余”代表相邻，表示直角三角形中与角相邻的直角边。
“切”有垂直之意，在圆的切线中有体现。
这样一来，正弦就是对边比斜边，余弦就是邻边比斜边，正切就是对边比（与对边垂直的）邻边。
我们常说切割，在数学里，切和割是相差很远的，比如切线和割线。所以在三角函数里，切割相反。

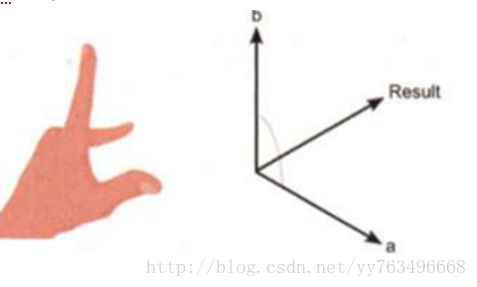
叉乘：两个向量的叉乘得到一个新的向量，新向量垂直与原来的两个向量，并且长度等于原来向量长度相乘后夹角的正弦值

注意：叉乘不满足交换律 即a×b 不等于 b×a。 

• 属性

  forward Vector3(0, 0, 1)的简码,也就是向z轴。 
  right Vector3(1, 0, 0)的简码,也就是向x轴。 
  up Vector3(0, 1, 0)的简码,也就是向y轴。 
  zero Vector3(0, 0, 0)的简码。 
  one 是 Vector3(1, 1, 1)的简码。 
  Vector3.sqrMagnitude 长度平方（只读的） 
  【注】计算长度的平方而不是magnitude是非常快的。如果你是比较两个向量的长度差，你可以比较他们的平方长度。 
  向量的长度是用勾股定理计算出来，计算机计算两次方和开根的运算量比加减法要费时的多。所以如果是想比较两个向量的长度，用sqrMagnitude可以快出很多。

• 向量运算

  向量加法 
  向量加法就是两个向量对应的x，y，z轴坐标进行加法运算 
  例如以下的代码

1.  
   Vector3 v1 = new Vector3(1, 2, 3);
2.  
   Vector3 v2 = new Vector3(4, 2, 1);
3.  
   Vector3 v3 = v1 + v2; //v3的结果 (5.0, 4.0, 4.0)
4.  
   Debug.Log(v3);

• 如果v1和v2都表示一个点的话，那么v3的方向是从v1开始指向v2的一个带有箭头的射线 此时v3就是一个向量 

如果v1和v2都表示一个向量的话，那么v3是一个从v1的尾部指向v2的头部的一个带有方向箭头的一条射线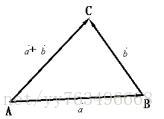 
 
向量减法 
向量加法就是两个向量对应的x，y，z轴坐标进行减法运算 
例如以下的代码

1.  
   Vector3 v1 = new Vector3(1, 2, 3);
2.  
   Vector3 v2 = new Vector3(4, 2, 1);
3.  
   Vector3 v3 = v2 - v1; //v3的结果 (3.0, 0.0, -2.0)
4.  
   Debug.Log(v3);

• 其实就是从向量b头部指向向量a头部的一个向量 

 
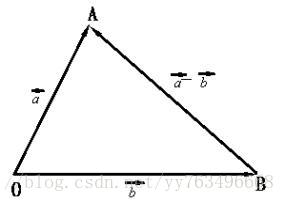
向量数乘 
实数和向量相乘的过程就是数乘 
如果实数大于0 那么数乘后的向量的方向和原始向量的方向一致，如果实数小于0 那么数乘后的向量的方向和原始向量的方向相反  
数乘的几何意义：就是沿着原始变量的方向或者变量的相反方向放大或者缩小

• 方法

  Vector3.Dot 点乘 （又称”点积”,”数量积”,”内积”）（Dot Product, 用＊） 
  定义：a·b=|a|·|b|cos< a,b> 【注：粗体小写字母表示向量，< a,b>表示向量a,b的夹角，取值范围为[0，180]】 
  几何意义：是一条边向另一条边的投影乘以另一条边的长度. 
  v1和v2向量的点乘运算：相应元素的乘积的和：v1( x1, y1，z1) v2(x2, y2,z2) = x1x2 + y1y2+z1z2; 
  注意 : 结果不是一个向量，而是一个标量。 
  性质1： ab = |a||b|Cos(θ) ，θ是向量a 和向量 b之间的夹角。 
  性质2： ab = b*a 满足乘法交换律 
  Unity项目应用： 
  1.根据点乘计算两个向量的夹角。< a,b>= arccos(a·b / (|a|·|b|)) 
  2.根据点乘的正负值，得到夹角大小范围，【大于>0，则夹角（0,90）】，【 小于<0,则夹角（90,180）】，可以利用这点判断一个多边形是面向摄像机还是背向摄像机。 
  3.根据点乘的大小，得到向量的投影长度，反应了向量的长度关系。 
  4.在生产生活中，点积同样应用广泛。利用点积可判断一个多边形是否面向摄像机还是背向摄像机。向量的点积与它们夹角的余弦成正比，因此在聚光灯的效果计算中，可以根据点积来得到光照效果，如果点积越大，说明夹角越小，则物理离光照的轴线越近，光照越强。物理中，点积可以用来计算合力和功。若b为单位矢量，则点积即为a在方向b的投影，即给出了力在这个方向上的分解。功即是力和位移的点积。计算机图形学常用来进行方向性判断，如两矢量点积大于0，则它们的方向朝向相近；如果小于0，则方向相反。矢量内积是人工智能领域中的神经网络技术的数学基础之一，此方法还被用于动画渲染（Animation-Rendering）。

  Vector3.Cross 叉乘 （又称”叉积”,”向量积”,”外积”）（cross product，用x） 
  定义：c = a x b，其中a b c均为向量 
  几何意义是：得到一个与这两个向量都垂直的向量，这个向量的模是以两个向量为边的平行四边形的面积 
  v1和v2向量的叉乘运算：相应元素的乘积的和：v1( x1, y1，z1) x v2(x2, y2, z2) = (y1z2 - y2z1)i+(x2z1 - x1z2)j+(x1y2-x2y1)k; 
  利用三阶行列式计算 
  |i j k| 
  |x1 y1 z1| 
  |x2 y2 z2| 
  性质1：c⊥a，c⊥b，即向量c与向量a，b所在平面垂直 
  性质2：模长|c| = |a||b| sin< a,b> 
  性质3：(数学上)满足右手法则, a x b = -b x a，所以我们可以使用叉乘的正负值来判断

  Unity当中叉乘的左手法则 
  Unity项目应用： 
  1.根据叉乘得到a，b向量的相对位置，和顺时针或逆时针方位。 
  简单的说: 点乘判断角度，叉乘判断方向。 
  形象的说: 当一个敌人在你身后的时候，叉乘可以判断你是往左转还是往右转更好的转向敌人，点乘得到你当前的面朝向的方向和你到敌人的方向的所成的角度大小。 
  2.得到a，b夹角的正弦值，计算向量的夹角（0,90），可以配合点乘和Angle方法计算出含正负的方向。 
  3.根据叉乘大小，得到a，b向量所形成的平行四边形的面积大小，根据面积大小得到向量的相对大小。

  Vector3.Distance 距离

  1.  
     void Test()
  2.  
     {
  3.  
     Vector3 v1 = new Vector3(0, 0, 2);
  4.  
     Vector3 v2 = new Vector3(2, 0, 0);
  5.  
     //求两个点之间的距离
  6.  
     Debug.Log(Vector3.Distance(v1,v2));
  7.  
      
  8.  
     }
  • Vector3.Lerp 插值 

  obj1的位置是上一帧的位置加上（目标位置-上一帧的位置）*0.1

obj1.transform.position = Vector3.Lerp(obj1.transform.position, obj2.transform.position, 0.1f);

• 1

Vector3.Normalize 规范化 
使向量编程长度为1的单位向量 
- Vector2和Vector4

Vector2 二维向量 
这个结构用于在一些地方表示2D的位置和向量（例如：网格中的纹理坐标，或者材质中的纹理偏移）。在其他情况下大多数使用Vector3。其操作基本可Vector3差不多 
静态变量 
one 
Vector2(1, 1)的简写。 
right 
Vector2(1, 0)的简写。 
up 
Vector2(0, 1)的简写。 
zero 
Vector2(0, 0)的简写。

Vector4 二维向量 
表示四维向量。 
这个结构在一些地方用来表示四维向量（例如：网格切线，着色器的参数）。在其他情况下大多数使用Vector3。 
其他操作和Vector3雷同

---

---

参考代码

点乘

1.  
   using System.Collections;
2.  
   using System.Collections.Generic;
3.  
   using UnityEngine;
4.  
    
5.  
   public class Vector3Test : MonoBehaviour {
6.  
    
7.  
   // Use this for initialization
8.  
   void Start () {
9.  
   Vector3 v1 = new Vector3(1, 0, 0);
10.  
    Vector3 v2 = new Vector3(1, 0, 1);
11.  
    TestDot(v1, v2);
12.  
    }
13.  
     
14.  
    // Update is called once per frame
15.  
    void Update () {
16.  
     
17.  
    }
18.  
     
19.  
    private void TestDot(Vector3 a,Vector3 b)
20.  
    {
21.  
    //计算两个向量点乘的结果 得到的是一个数值
22.  
    //求得的是向量b在向量a方向上的投影
23.  
    float result = Vector3.Dot(a,b);
24.  
    Debug.Log("Result = "+result);
25.  
    //计算两个向量的夹角，该方法得到的是一个角度 计算出来的夹角的范围是0-180度
26.  
    float angle = Vector3.Angle(a,b);
27.  
    Debug.Log("angle = " + angle);
28.  
    //向量b方向上的单位向量在向量a方向单位向量的投影
29.  
    //计算 a、b 单位向量的点积,得到夹角余弦值,|a.normalized|*|b.normalized|=1;
30.  
    result = Vector3.Dot(a.normalized,b.normalized);
31.  
    Debug.Log("result = " + result);
32.  
    // 通过反余弦函数获取 向量 a、b 夹角（默认为 弧度）
33.  
    float radians = Mathf.Acos(result);
34.  
    angle = radians * Mathf.Rad2Deg;
35.  
    Debug.Log(angle);
36.  
    }
37.  
     
38.  
    }

• 叉乘