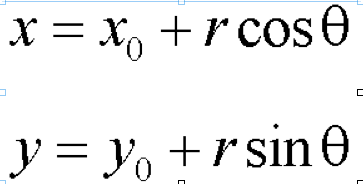霍夫曼圆变换

转自：

https://www.cnblogs.com/zkwarrior/p/4990477.html

https://blog.csdn.net/jia20003/article/details/17252807

首先是研究线变换。直线在笛卡尔坐标系里面是y = k * x + b。

在笛卡尔坐标系中作图

可得：

化简可得：

则对于给定点（x0,y0)不同的r和θ代表经过该点的不同的直线，当(x0,y0)确定则r与θ成正弦函数图像。当在坐标系中画出不同的（x,y）对应的正弦函数图像时，交点则代表经过不同的点的同一条直线，则可以通过对应于某一点（θ，r）相交的正弦曲线的数量，来表示此直线通过图像中多少个点，通过设定点数量的阈值来判定是否是一条直线。

同理对于圆来说                  

圆可以表示为如上形式

对于存在在图形上的像素点，已知r则以该点为圆心转360°，对于经过的每一个点叠加，达到阈值的则认为该点为圆心此处附上源码

    /**
     * 霍夫变换处理 - 检测半径大小符合的圆的个数
     * 1. 将图像像素从2D空间坐标转换到极坐标空间
     * 2. 在极坐标空间中归一化各个点强度，使之在0〜255之间
     * 3. 根据极坐标的R值与输入参数(圆的半径)相等，寻找2D空间的像素点
     * 4. 对找出的空间像素点赋予结果颜色(红色)
     * 5. 返回结果2D空间像素集合
     * @return int []
     */
    public int[] process() {

        // 对于圆的极坐标变换来说，我们需要360度的空间梯度叠加值
        acc = new int[width * height];
        for (int y = 0; y < height; y++) {
            for (int x = 0; x < width; x++) {
                acc[y * width + x] = 0;
            }
        }
        int x0, y0;
        double t;
        for (int x = 0; x < width; x++) {
            for (int y = 0; y < height; y++) {

                if ((input[y * width + x] & 0xff) == 255) {//估计是判断是否存在

                    for (int theta = 0; theta < 360; theta++) {
                        t = (theta * 3.14159265) / 180; // 角度值0 ~ 2*PI
                        x0 = (int) Math.round(x - r * Math.cos(t));
                        y0 = (int) Math.round(y - r * Math.sin(t));
                        if (x0 < width && x0 > 0 && y0 < height && y0 > 0) {
                            acc[x0 + (y0 * width)] += 1;
                        }
                    }
                }
            }
        }

        // now normalise to 255 and put in format for a pixel array
        int max = 0;

        // Find max acc value
        for (int x = 0; x < width; x++) {
            for (int y = 0; y < height; y++) {

                if (acc[x + (y * width)] > max) {
                    max = acc[x + (y * width)];
                }
            }
        }

        // 根据最大值，实现极坐标空间的灰度值归一化处理
        int value;
        for (int x = 0; x < width; x++) {
            for (int y = 0; y < height; y++) {
                value = (int) (((double) acc[x + (y * width)] / (double) max) * 255.0);
                acc[x + (y * width)] = 0xff000000 | (value << 16 | value << 8 | value);
            }
        }
        
        // 绘制发现的圆
        findMaxima();
        System.out.println("done");
        return output;
    }

package com.gloomyfish.image.transform.hough;
/***
 * 
 * 传入的图像为二值图像，背景为黑色，目标前景颜色为为白色
 * @author gloomyfish
 * 
 */
public class CircleHough {

    private int[] input;
    private int[] output;
    private int width;
    private int height;
    private int[] acc;//（记录每个像素点灰度值）
    private int accSize = 1;
    private int[] results;
    private int r; // 圆周的半径大小

    public CircleHough() {
        System.out.println("Hough Circle Detection...");
    }

    public void init(int[] inputIn, int widthIn, int heightIn, int radius) {
        r = radius;
        width = widthIn;
        height = heightIn;
        input = new int[width * height];
        output = new int[width * height];
        input = inputIn;
        for (int y = 0; y < height; y++) {
            for (int x = 0; x < width; x++) {
                output[x + (width * y)] = 0xff000000; //默认图像背景颜色为黑色
            }
        }
    }

    public void setCircles(int circles) {
        accSize = circles; // 需要检测的圆的个数
    }
    
    /**
     * 霍夫变换处理 - 检测半径大小符合的圆的个数
     * 1. 将图像像素从2D空间坐标转换到极坐标空间
     * 2. 在极坐标空间中归一化各个点强度，使之在0〜255之间
     * 3. 根据极坐标的R值与输入参数(圆的半径)相等，寻找2D空间的像素点
     * 4. 对找出的空间像素点赋予结果颜色(红色)
     * 5. 返回结果2D空间像素集合
     * @return int []
     */
    public int[] process() {

        // 对于圆的极坐标变换来说，我们需要360度的空间梯度叠加值
        acc = new int[width * height];
        for (int y = 0; y < height; y++) {
            for (int x = 0; x < width; x++) {
                acc[y * width + x] = 0;
            }
        }
        int x0, y0;
        double t;
        for (int x = 0; x < width; x++) {
            for (int y = 0; y < height; y++) {

                if ((input[y * width + x] & 0xff) == 255) {

                    for (int theta = 0; theta < 360; theta++) {
                        t = (theta * 3.14159265) / 180; // 角度值0 ~ 2*PI
                        x0 = (int) Math.round(x - r * Math.cos(t));
                        y0 = (int) Math.round(y - r * Math.sin(t));
                        if (x0 < width && x0 > 0 && y0 < height && y0 > 0) {
                            acc[x0 + (y0 * width)] += 1;
                        }
                    }
                }
            }
        }

        // now normalise to 255 and put in format for a pixel array
        int max = 0;

        // Find max acc value
        for (int x = 0; x < width; x++) {
            for (int y = 0; y < height; y++) {

                if (acc[x + (y * width)] > max) {
                    max = acc[x + (y * width)];
                }
            }
        }

        // 根据最大值，实现极坐标空间的灰度值归一化处理
        int value;
        for (int x = 0; x < width; x++) {
            for (int y = 0; y < height; y++) {
                value = (int) (((double) acc[x + (y * width)] / (double) max) * 255.0);
                acc[x + (y * width)] = 0xff000000 | (value << 16 | value << 8 | value);
            }
        }
        
        // 绘制发现的圆
        findMaxima();
        System.out.println("done");
        return output;
    }

    private int[] findMaxima() {
        results = new int[accSize * 3];
        int[] output = new int[width * height];
        
        // 获取最大的前accSize个值
        for (int x = 0; x < width; x++) {
            for (int y = 0; y < height; y++) {
                int value = (acc[x + (y * width)] & 0xff);

                // if its higher than lowest value add it and then sort
                if (value > results[(accSize - 1) * 3]) {

                    // add to bottom of array
                    results[(accSize - 1) * 3] = value; //像素值
                    results[(accSize - 1) * 3 + 1] = x; // 坐标X
                    results[(accSize - 1) * 3 + 2] = y; // 坐标Y

                    // shift up until its in right place
                    int i = (accSize - 2) * 3;
                    while ((i >= 0) && (results[i + 3] > results[i])) {
                        for (int j = 0; j < 3; j++) {
                            int temp = results[i + j];
                            results[i + j] = results[i + 3 + j];
                            results[i + 3 + j] = temp;
                        }
                        i = i - 3;
                        if (i < 0)
                            break;
                    }
                }
            }
        }

        // 根据找到的半径R，中心点像素坐标p(x, y)，绘制圆在原图像上
        System.out.println("top " + accSize + " matches:");
        for (int i = accSize - 1; i >= 0; i--) {
            drawCircle(results[i * 3], results[i * 3 + 1], results[i * 3 + 2]);
        }
        return output;
    }

    private void setPixel(int value, int xPos, int yPos) {
        /// output[(yPos * width) + xPos] = 0xff000000 | (value << 16 | value << 8 | value);
        output[(yPos * width) + xPos] = 0xffff0000;
    }

    // draw circle at x y
    private void drawCircle(int pix, int xCenter, int yCenter) {
        pix = 250; // 颜色值，默认为白色

        int x, y, r2;
        int radius = r;
        r2 = r * r;
        
        // 绘制圆的上下左右四个点
        setPixel(pix, xCenter, yCenter + radius);
        setPixel(pix, xCenter, yCenter - radius);
        setPixel(pix, xCenter + radius, yCenter);
        setPixel(pix, xCenter - radius, yCenter);

        y = radius;
        x = 1;
        y = (int) (Math.sqrt(r2 - 1) + 0.5);
        
        // 边缘填充算法， 其实可以直接对循环所有像素，计算到做中心点距离来做，大概是x左右移时用勾股定理加上图像处理只能在像素点上
        // 这个方法是别人写的，发现超赞，超好！
        while (x < y) {
            setPixel(pix, xCenter + x, yCenter + y);
            setPixel(pix, xCenter + x, yCenter - y);
            setPixel(pix, xCenter - x, yCenter + y);
            setPixel(pix, xCenter - x, yCenter - y);
            setPixel(pix, xCenter + y, yCenter + x);
            setPixel(pix, xCenter + y, yCenter - x);
            setPixel(pix, xCenter - y, yCenter + x);
            setPixel(pix, xCenter - y, yCenter - x);
            x += 1;
            y = (int) (Math.sqrt(r2 - x * x) + 0.5);
        }
        if (x == y) {
            setPixel(pix, xCenter + x, yCenter + y);
            setPixel(pix, xCenter + x, yCenter - y);
            setPixel(pix, xCenter - x, yCenter + y);
            setPixel(pix, xCenter - x, yCenter - y);
        }
    }

    public int[] getAcc() {
        return acc;
    }

}