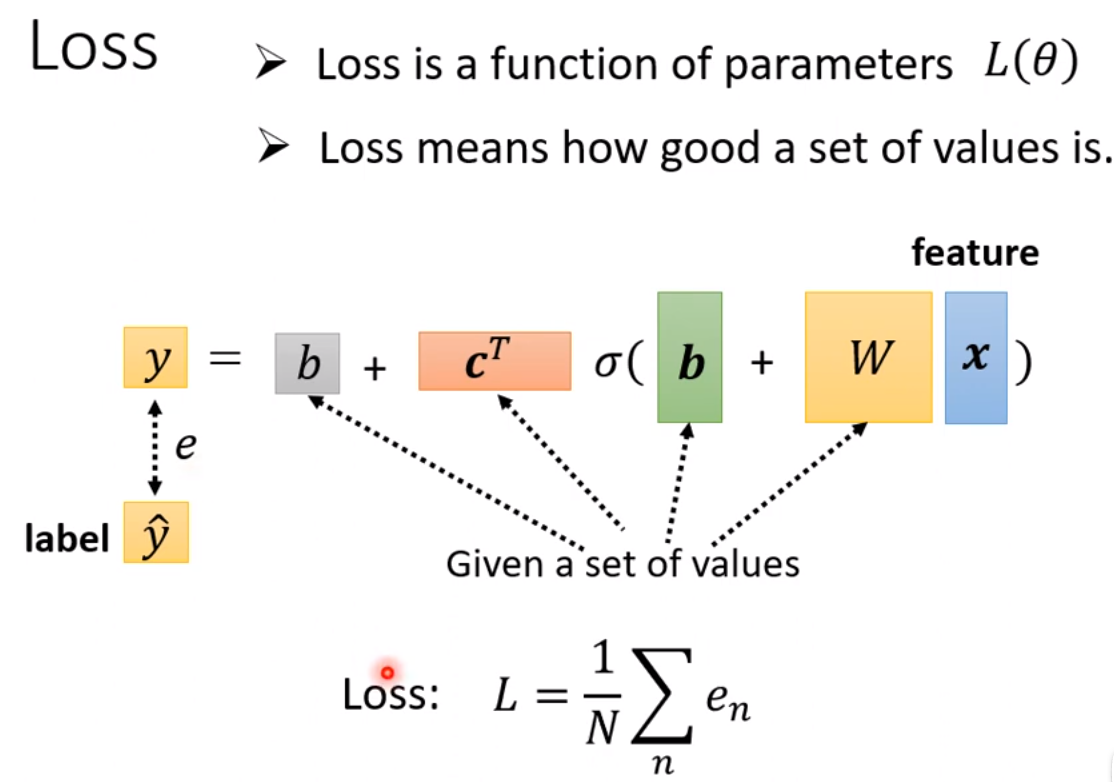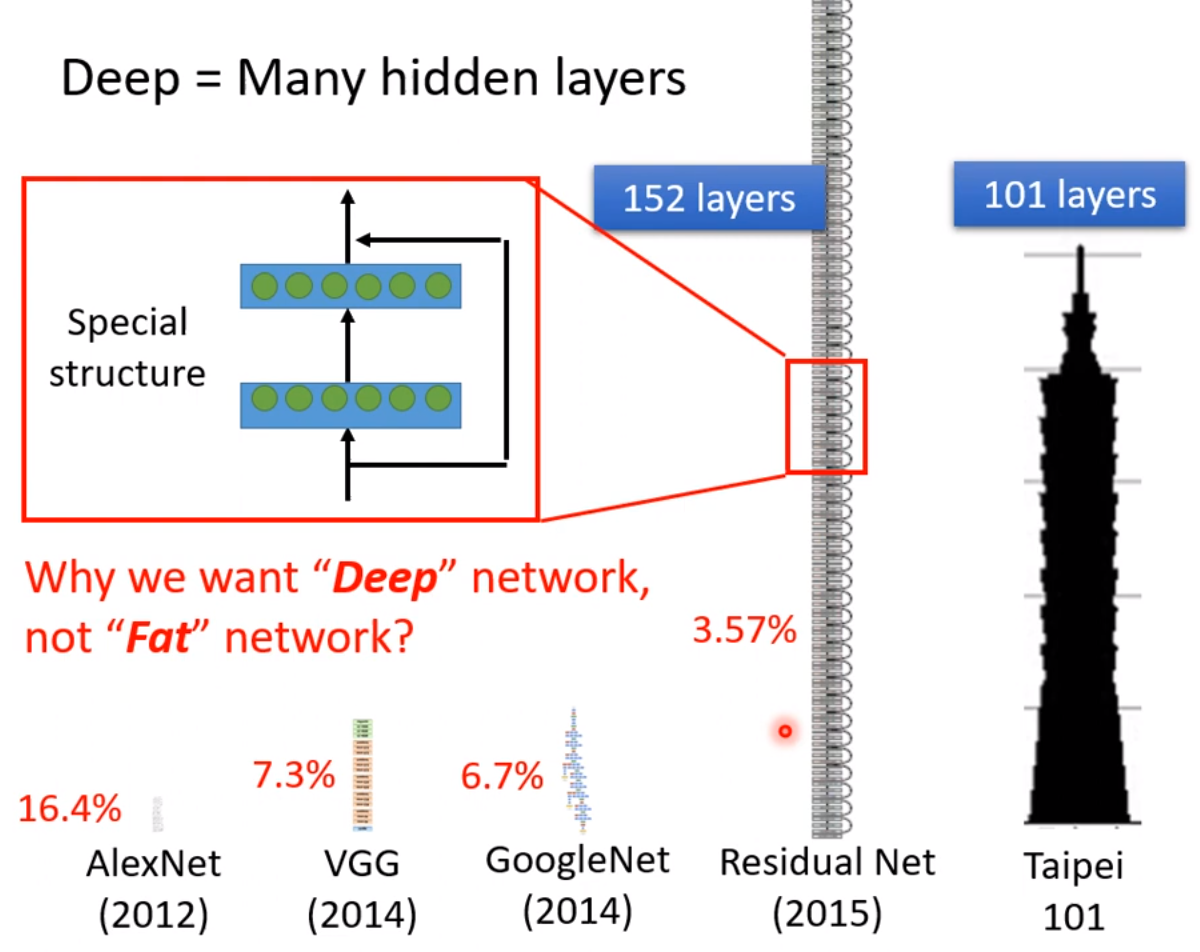






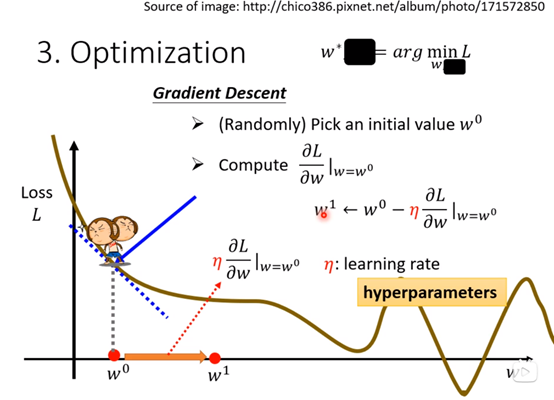
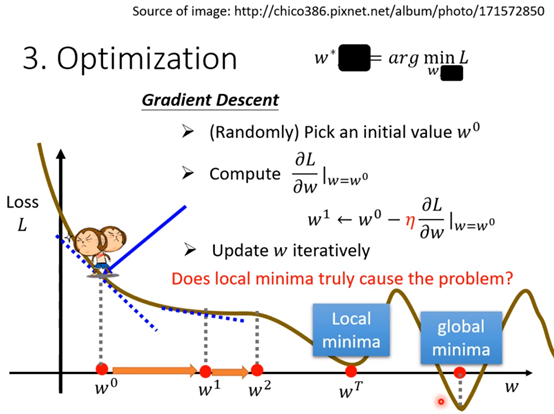

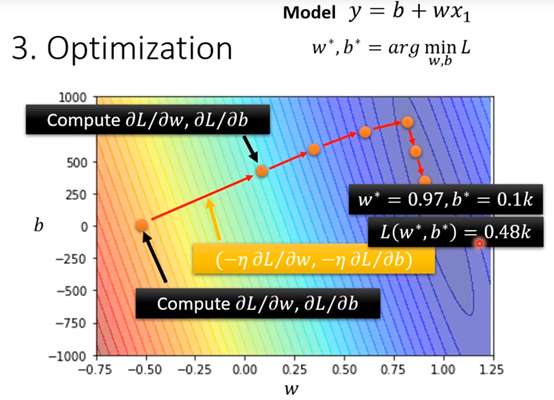
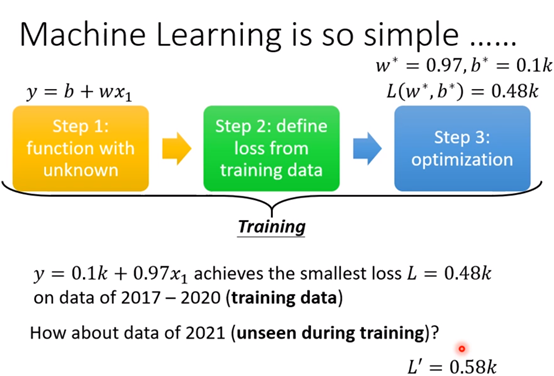

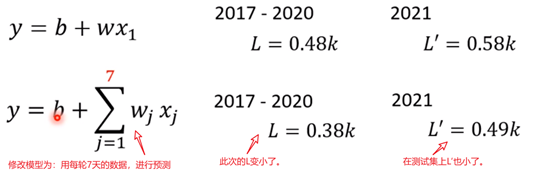


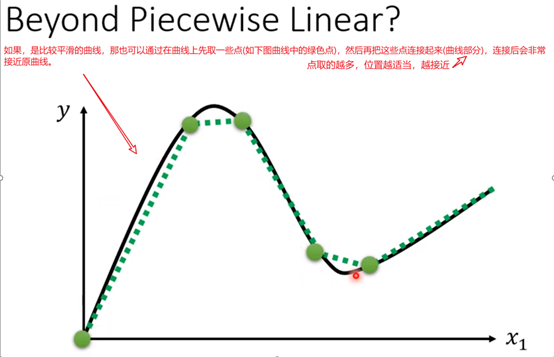



上图中通过三个参数单独的改变,sigmoid函数的图形也在不断的变化,改变w-->斜率,改变b-->图像平移(可能是上下左右),改变c-->改变了图形的高度。
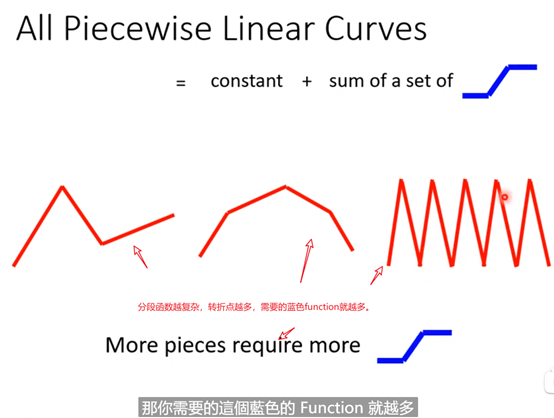
所以,只要有不同的w,b,c就可以生成不同的sigmoid function叠起来后,就可以逼近各种不同的piecewise linear的function,然后Piecewise linear function可以拿来近似
各种不同continuous的function。
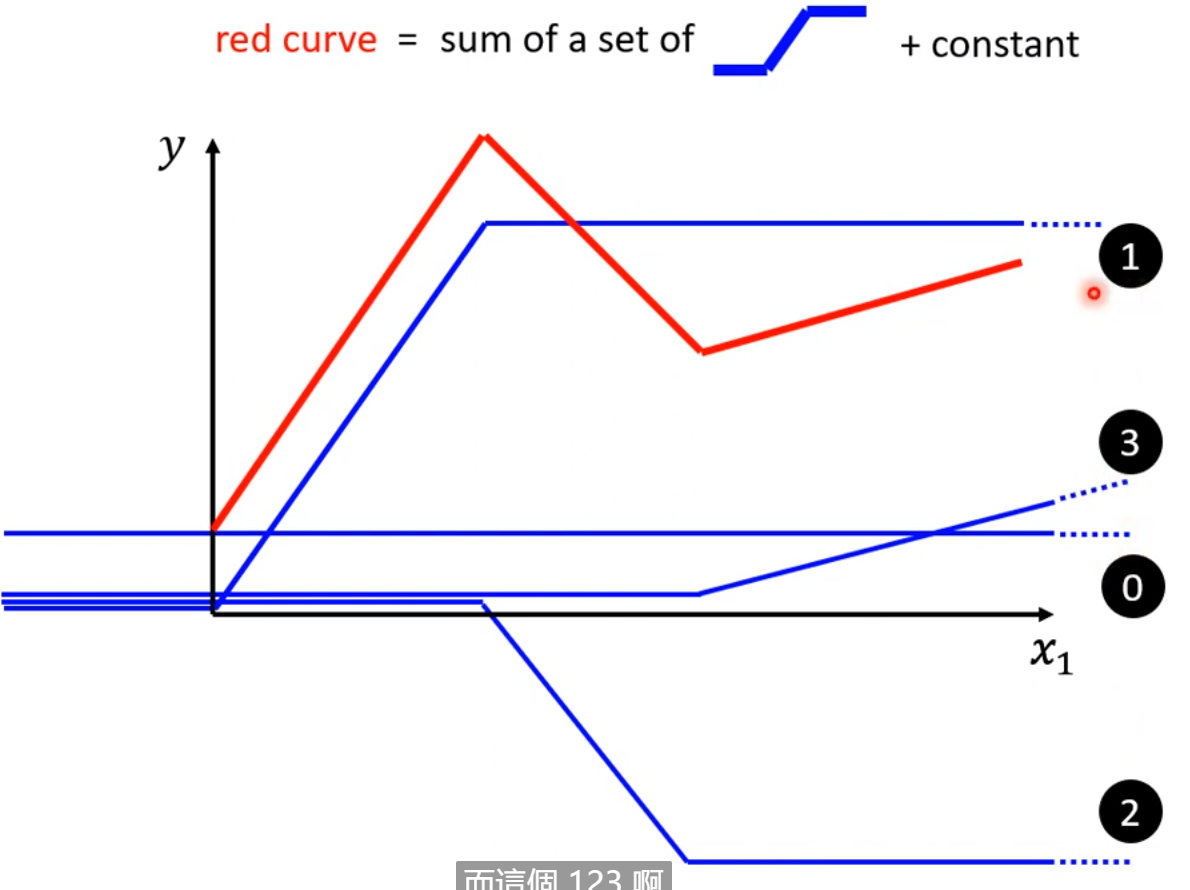
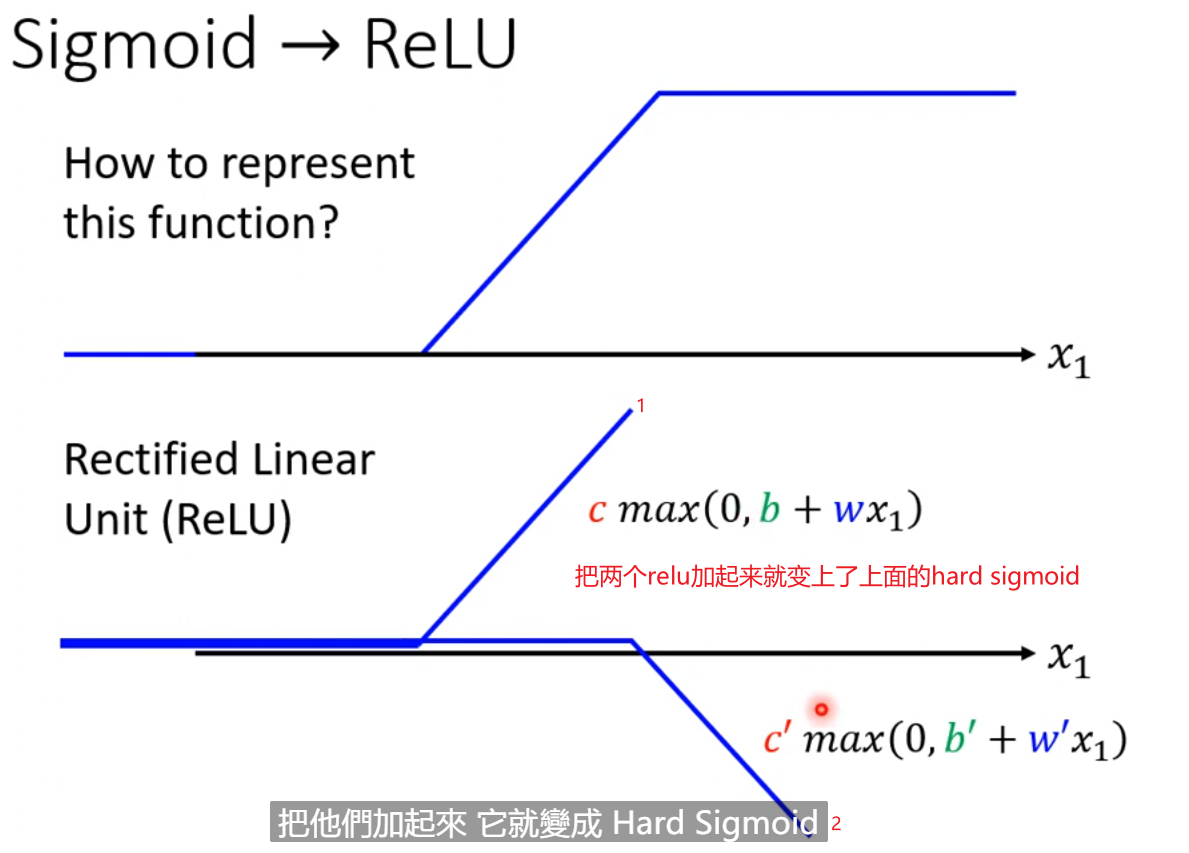
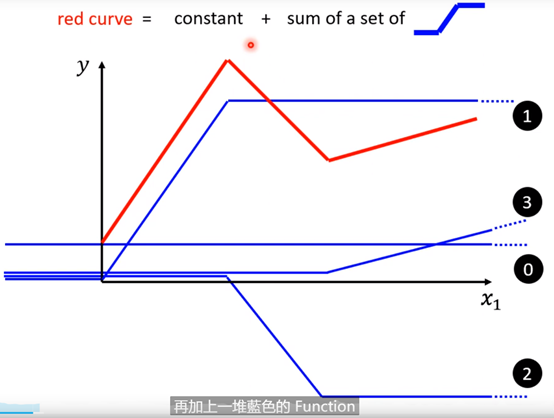
上图中红色的线,可以表示成0+1+2+3号线,而0,1,2,3号线它们都是蓝色的function,它们都有一个固定的样子,它们都写作C*Sigmoid(b+w*x),只不过它们的
w和b不一样而已。如下图示:
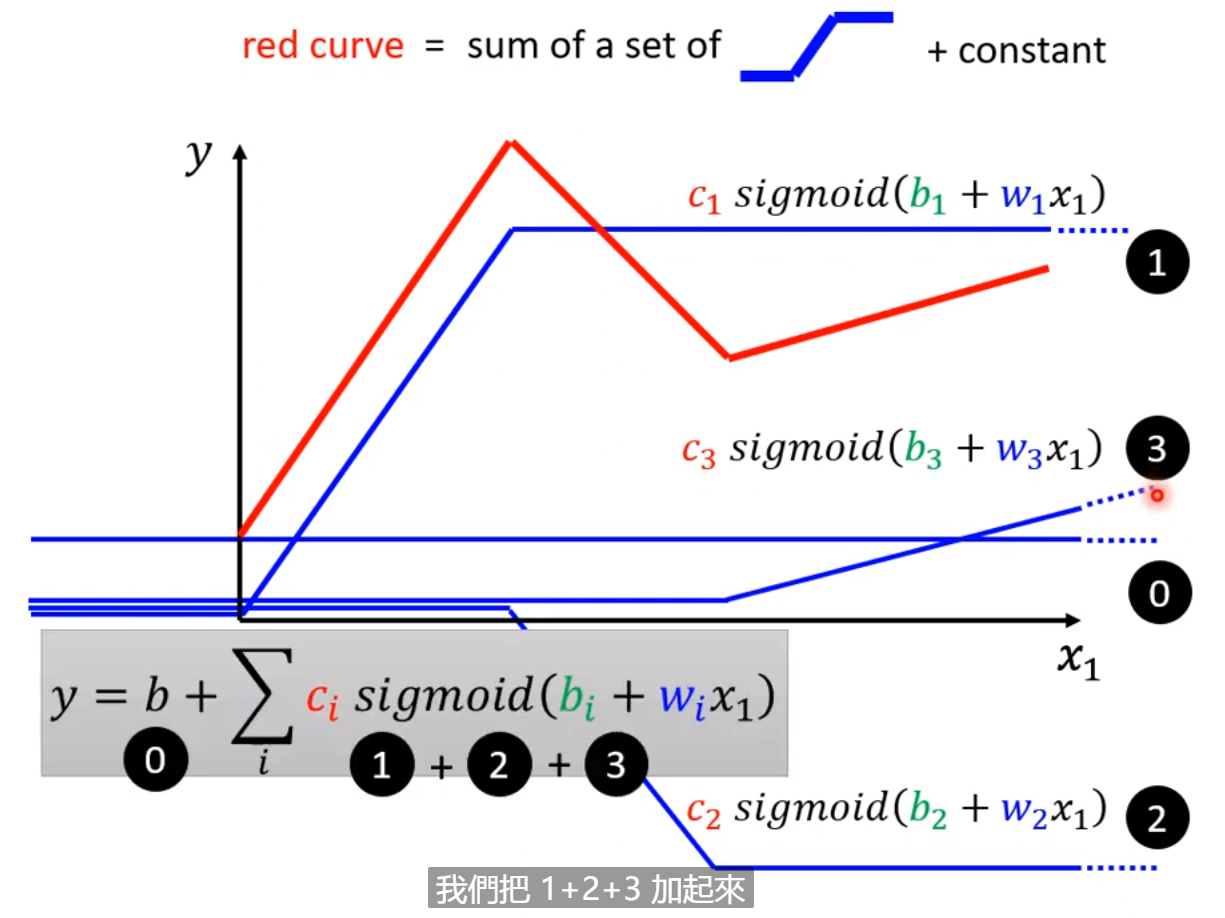
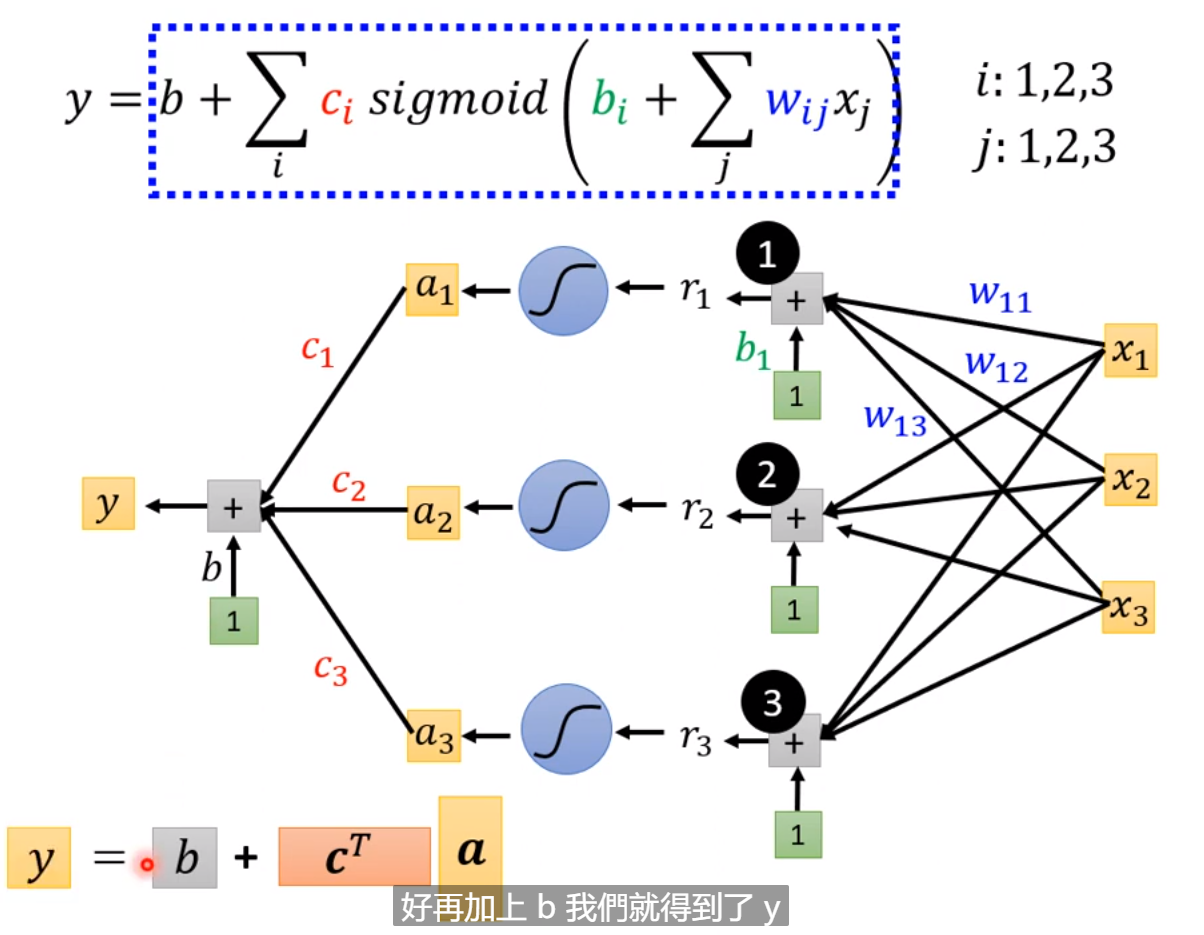
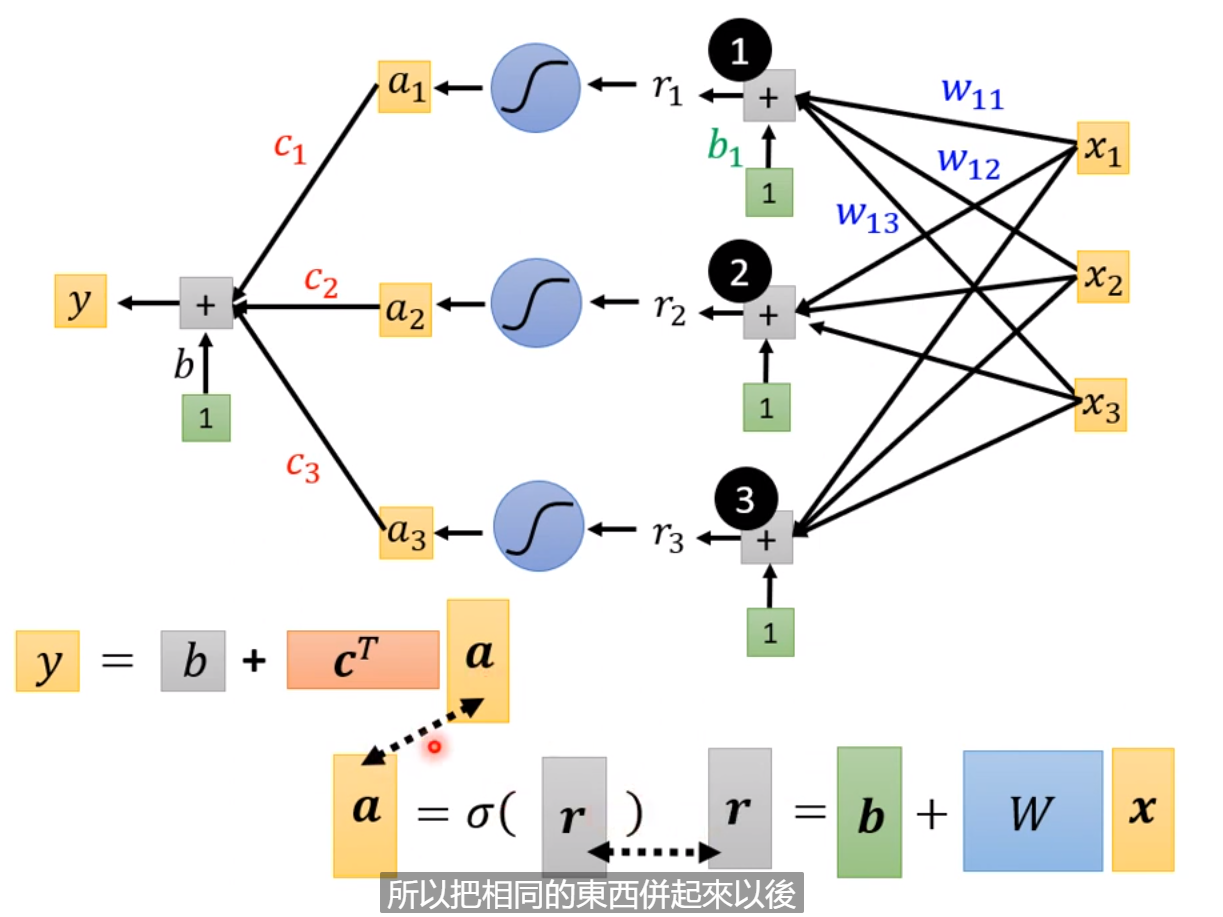
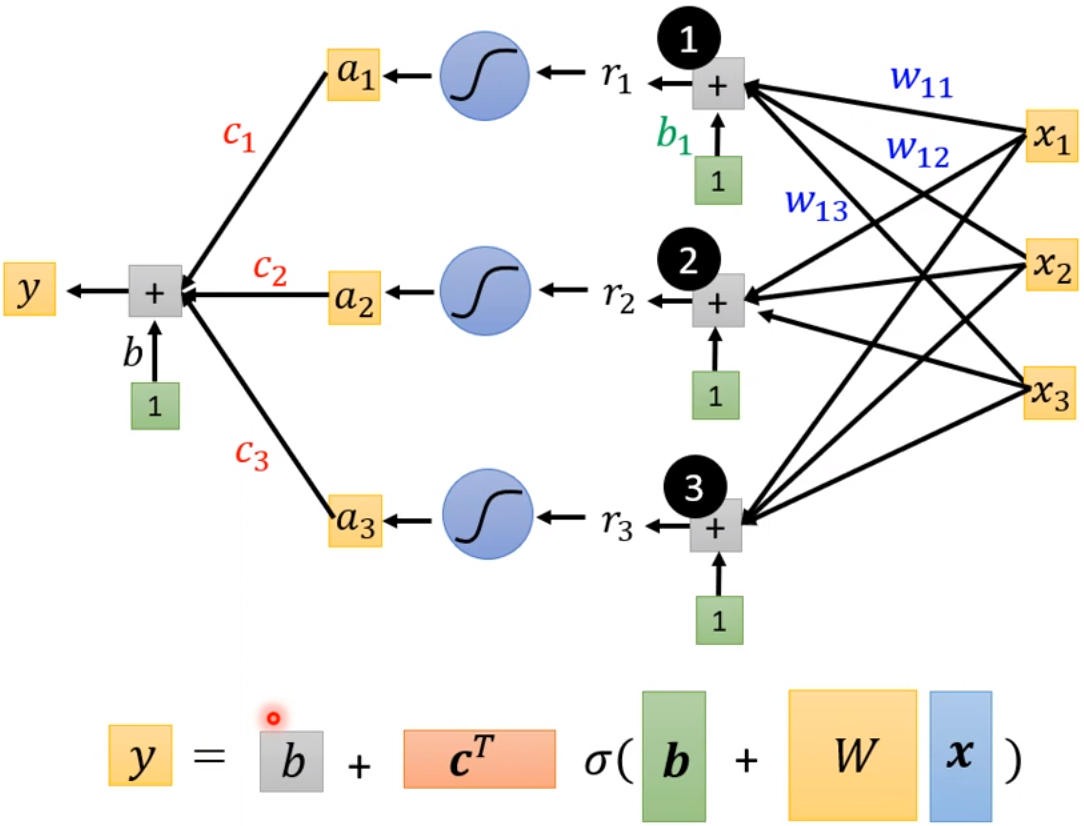
设定上图中的不同的bi,ci,wi就可以生成不同的蓝色function,不同的蓝色function叠起来以后就可以制造出红色的Curves,不同的红色Curves又可以制造出不同的Piecewise Linear的Curves,进而用不同的Piecewise Linear Curves逼近各种各样不同的Continuous的function。也即其实我们可以有办法写出非常有弹性有未知参数的function,即上图中所示的y=b+sigma(ci*sigmoid(bi+wi*x1)).
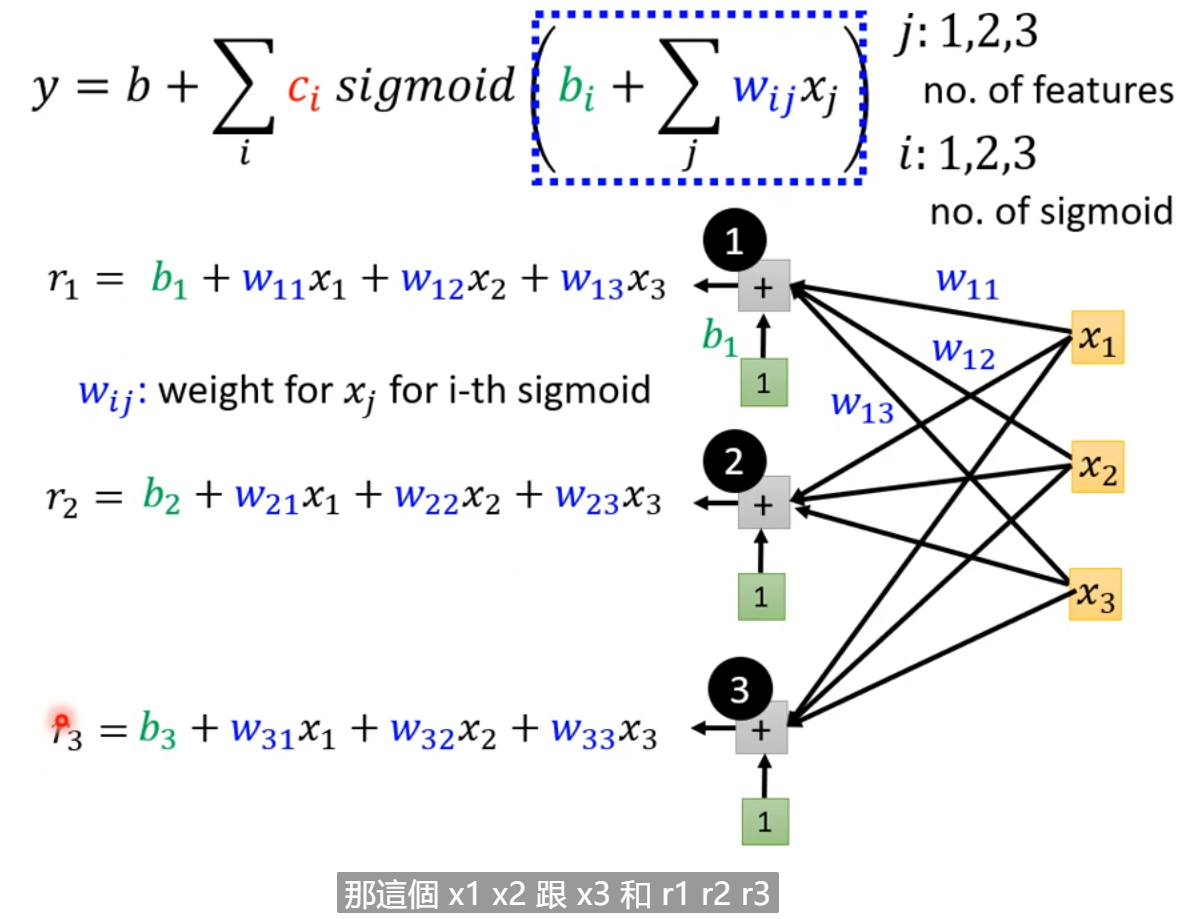
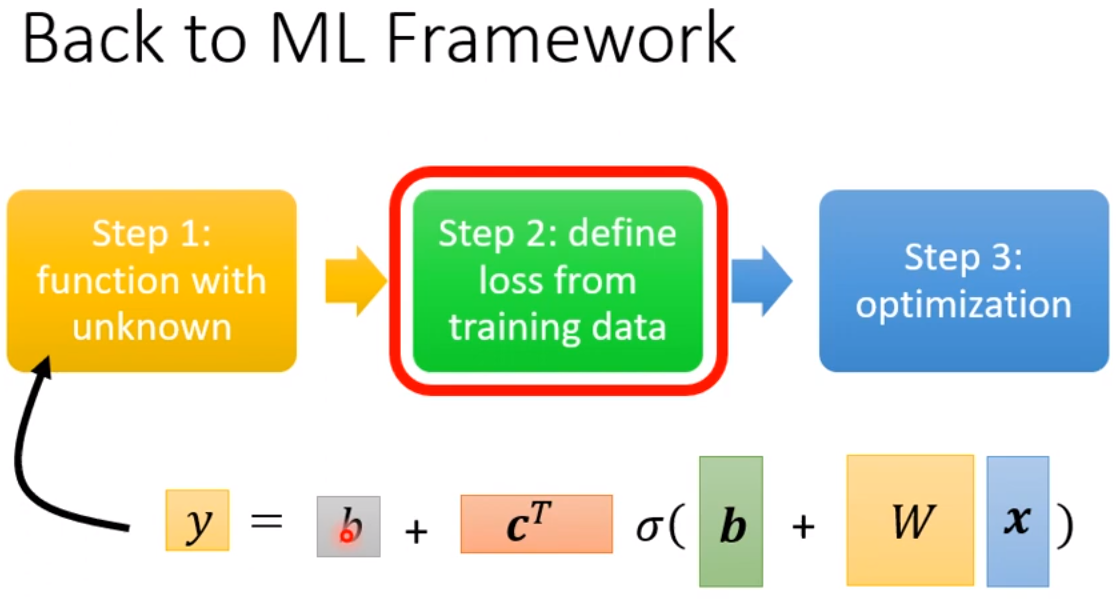
所以,本来的线性模型y=b+w*x,它有非常的限制,这个限制就叫做model的bias,可以写成下图的更有弹性、有未知参数的式子。
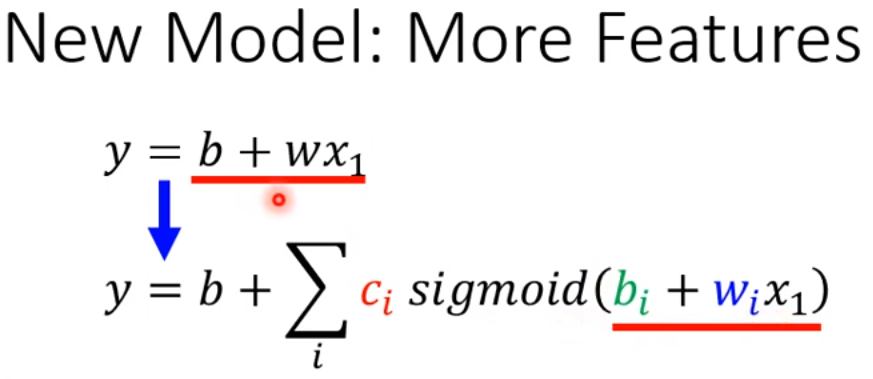
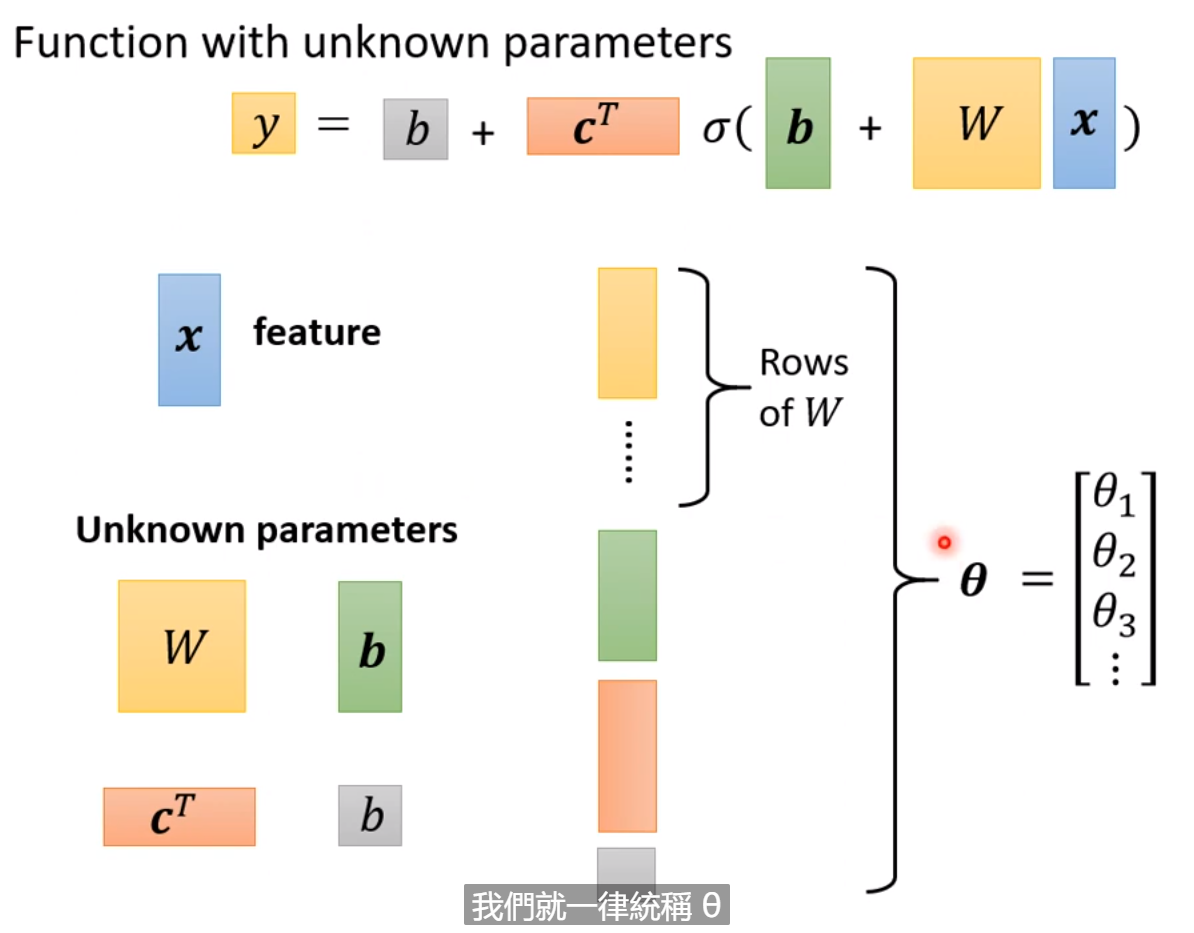
上式,只要带入不同的bi,xi,wi就可以组合成不同的function,
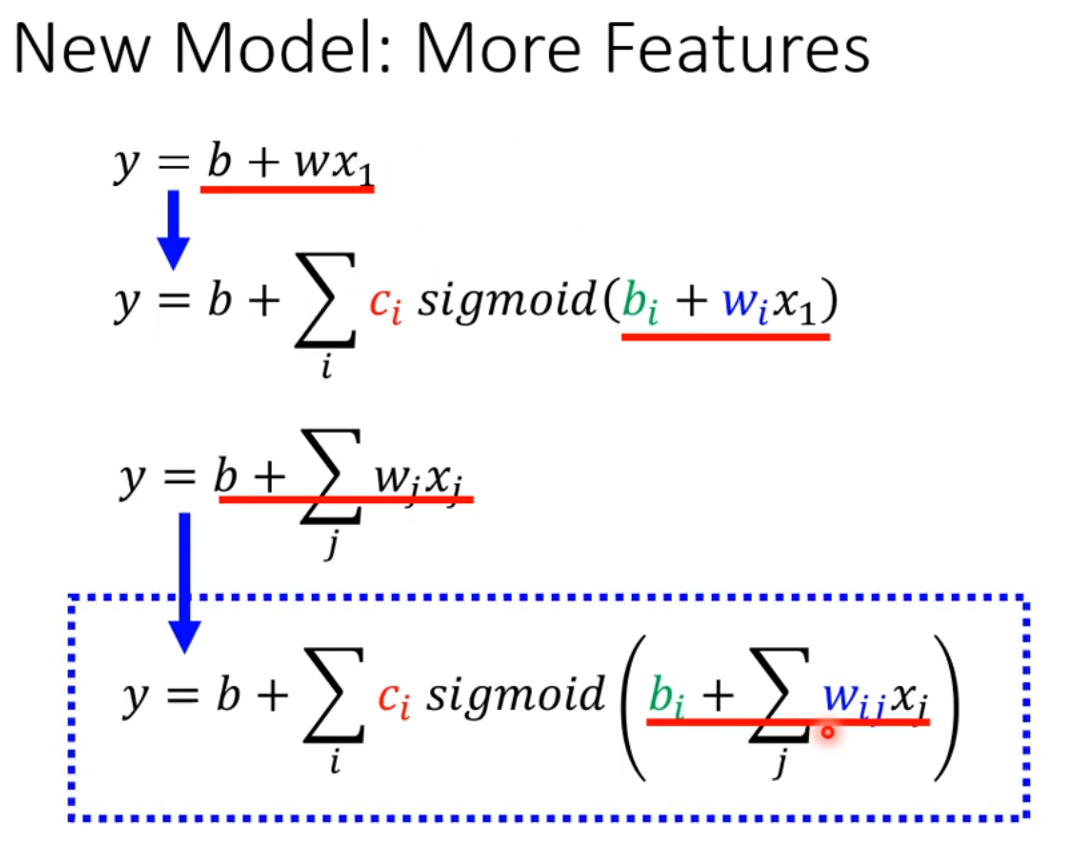
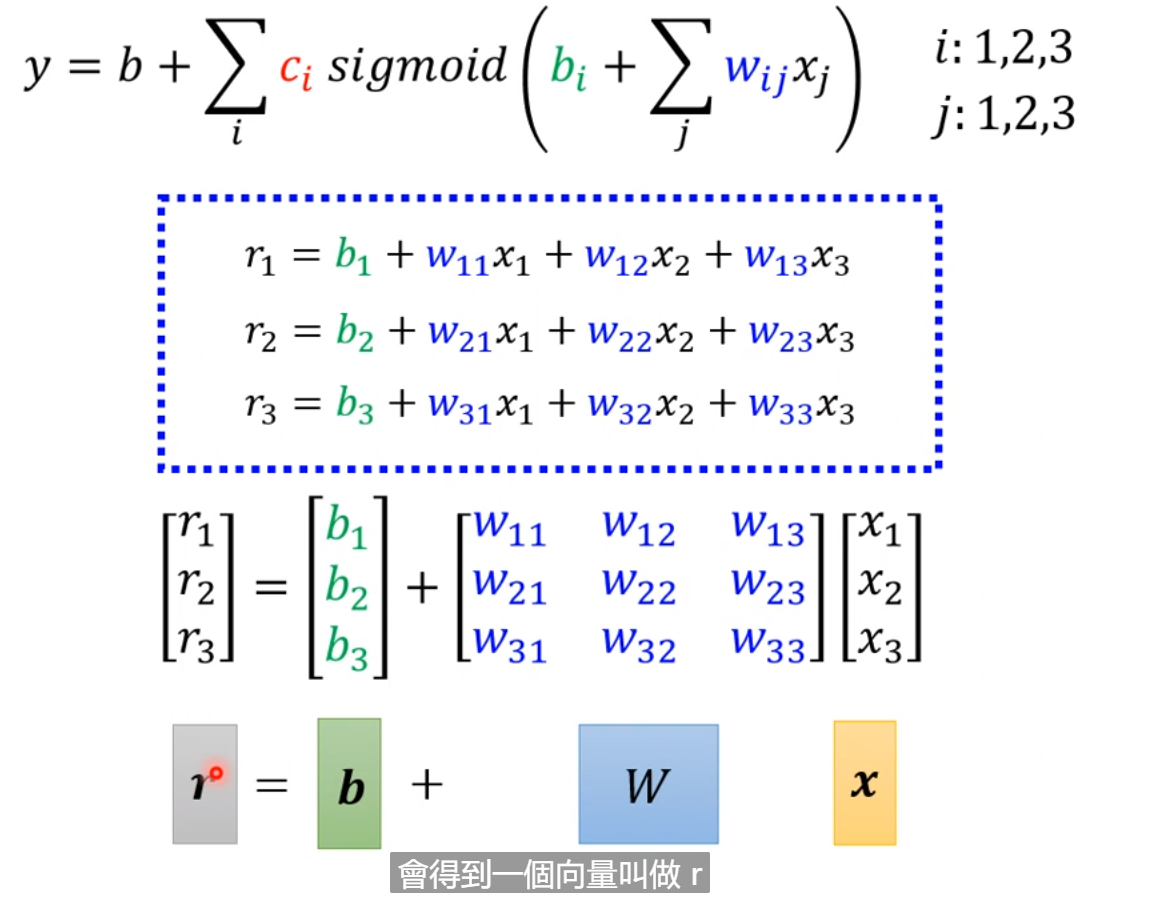
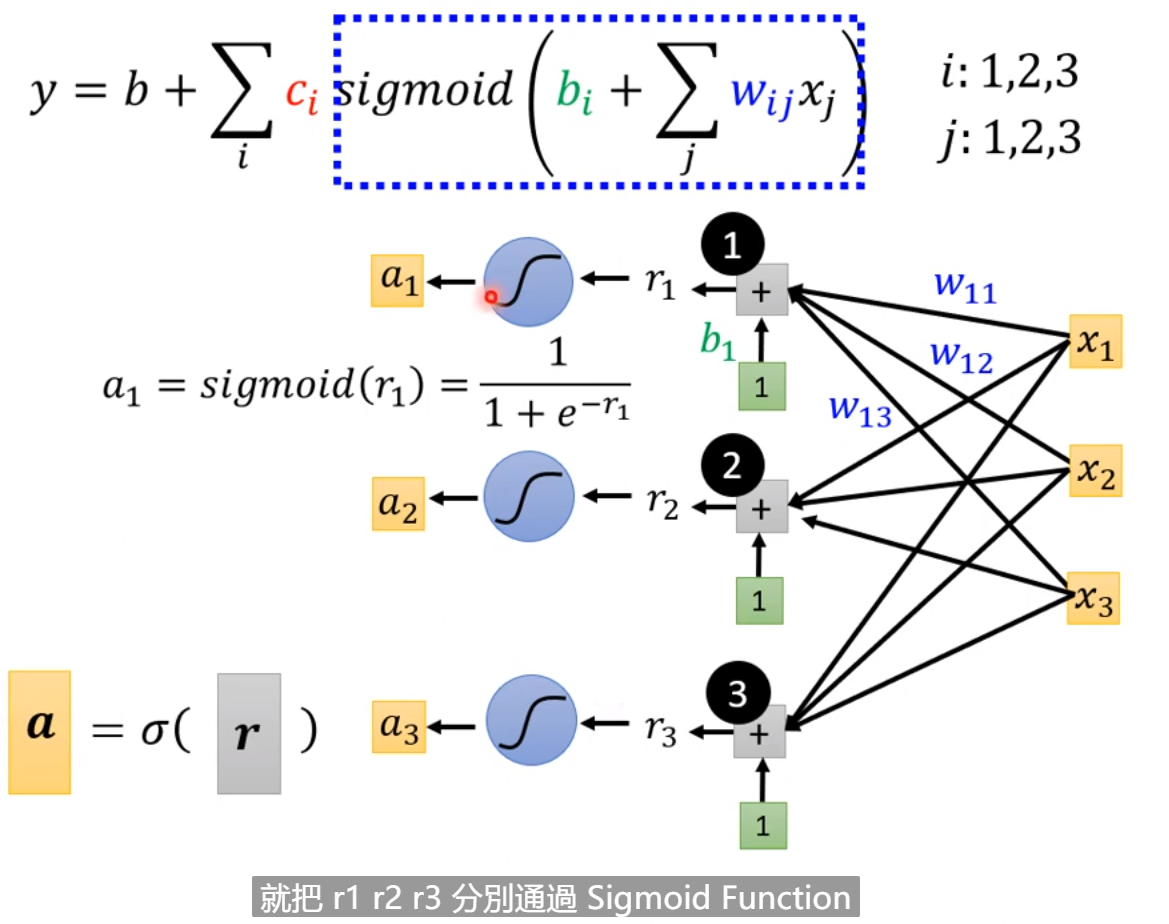
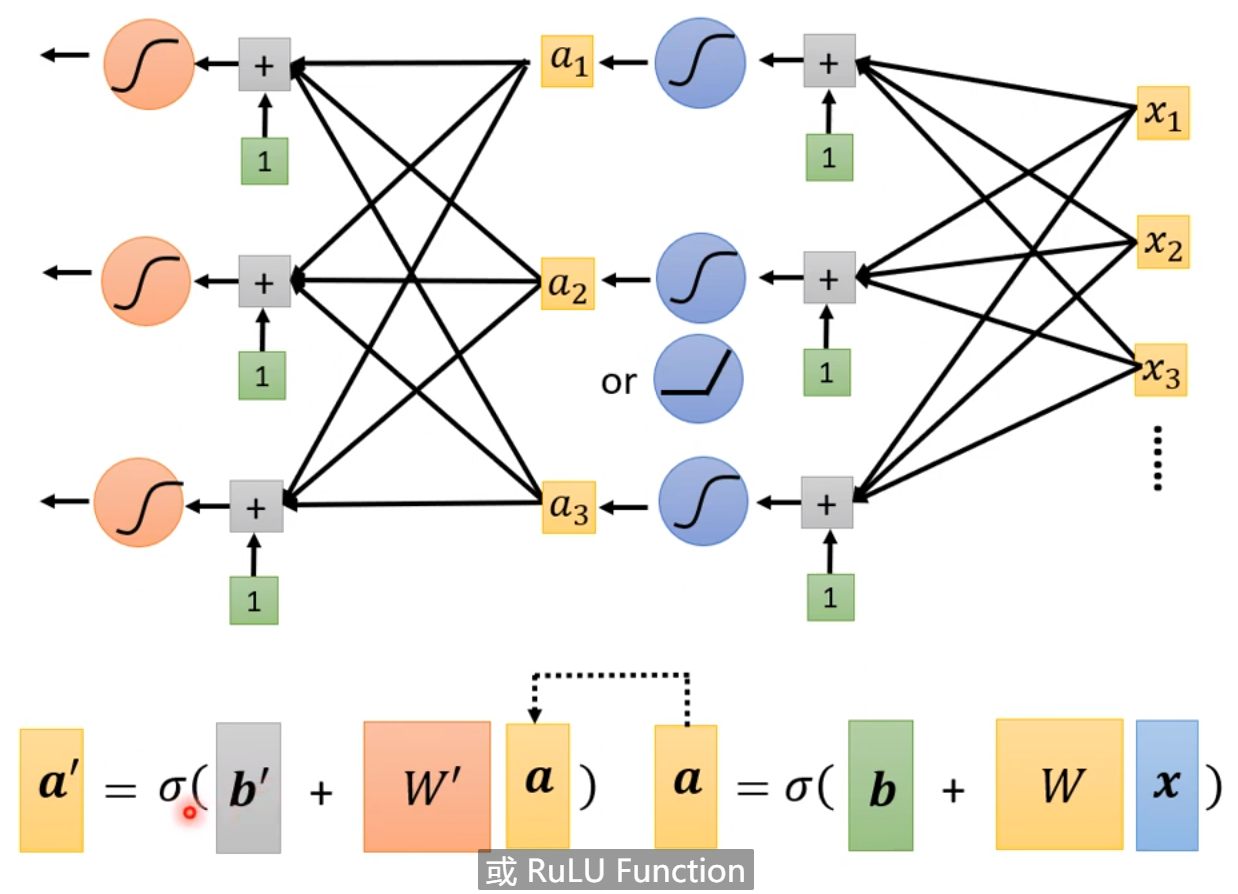
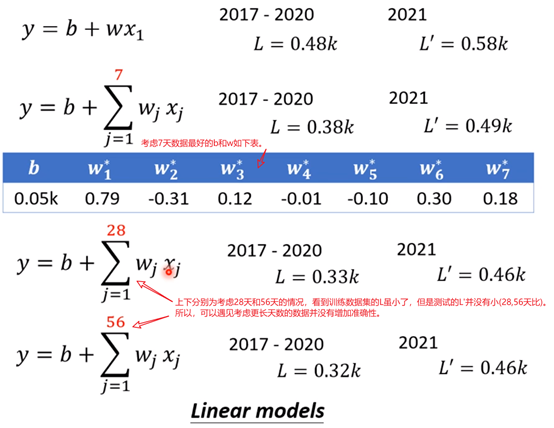
例子中我们也可以考虑多个feature而不是1个feature,所以,进而可以把上图中第一个式子改为第三个(e.g.如果不是只考虑1天而考虑,7,28,56天,那么j也就是7,28,56),进而第二个式子变为第四个式子。即用第三个式子替换第二个式子sigmoid里面的项,就变味了第四个式子。