快速排序

《算法导论》第七章----快速排序（代码实现+部分练习+部分证明）

 

快速排序，对于n个数的输入数组，最坏情况运行时间：Θ(n^2)；期望运行时间：Θ(nlgn)；就地排序（Sort in place）。

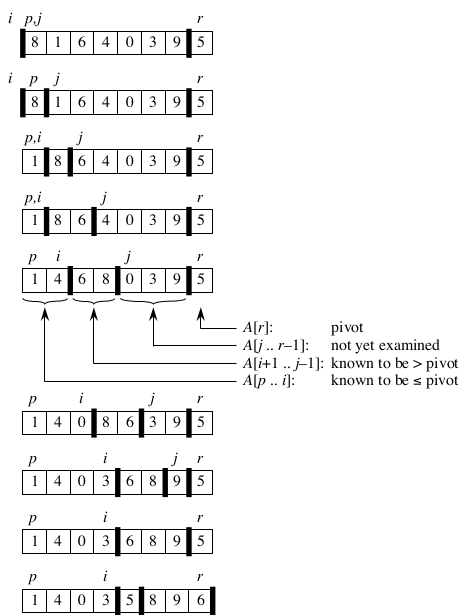
数组A[p..r]会被分为两个子数组A[p..q-1]和A[q+1..r]，其中A[p..q-1]的元素都不大于A[q]，A[q+1..r]都不小于A[q]。

如何划分子数组对运行时间的有很大影响，最坏的情况为n个数的数组划分为一个n-1的数组和一个0元素的数组；最佳情况为对半分（1：1）；对于平均情况的划分，其运行时间与最佳情况很接近。

先看代码实现：

快速排序的关键是数组划分，对子数组进行就地重排。

int randomized_partition(int A[], int p, int r){
int i = p + rand() % (r - p + 1);
int temp = A[r];
A[r] = A[i];
A[i] = temp;
return partition(A, p, r);
}

int partition(int A[], int p, int r){
int x = A[r];
int i = p - 1;
int j;
for(j = p; j <= r-1; j++){
if(A[j] <= x){
i++;
int temp = A[i];
A[i] = A[j];
A[j] = temp;
}
}
int temp = A[i+1];
A[i+1] = A[r];
A[r] = temp;
return i+1;
}

void randomized_quick_sort(int A[], int p, int r){
if(p < r){
int q = randomized_partition(A, p, r);
randomized_quick_sort(A, p, q-1);
randomized_quick_sort(A, q+1, r);
}
}

 1 /*
 2  * 调用划分函数，使得子数组顺序重排
 3  */
 4 void quick_sort(int A[], int p, int r){
 5     if(p < r){
 6         int q = partition(A, p, r);
 7         quick_sort(A, p, q-1);
 8         quick_sort(A, q+1, r);
 9     }
10 }
11 
12 /*
13  * 对于比x值小的元素通过交换放置到小于x值的区域。
14  * 最后将大于x值的区域的第一个元素与x值，即原A[r]，交换
15  * 该下标即为q，形成两个符合要求的数组（A[p..q-1]的元素都不大于A[q]，A[q+1..r]都不小于A[q]）
16  */
17 int partition(int A[], int p, int r){
18     int x = A[r];
19     int i = p - 1;
20     int j;
21     for(j = p; j <= r-1; j++){
22         if(A[j] <= x){
23             i++;
24             int temp = A[i];
25             A[i] = A[j];
26             A[j] = temp;
27         }
28     }
29     int temp = A[i+1];
30     A[i+1] = A[r];
31     A[r] = temp;
32     return i+1;
33 }

其中partition的运行时间为Θ(n)，n = r-p+1，循环的次数为r-1-p；

过程图如下：

练习7.1-2

当数组A[p..r]中的元素均相同时，partition返回的q值是多少？修改partition，使得数组A[p..r]中的元素均相同时， q = floor((p+r)/2)

当数组A[p..r]中的元素均相同时，partition返回的q值是r；修改很简单，直接判断返回的q值是否与r相同，相同就返回 floor((p+r)/2)。

 

快速排序的性能

快速排序的运行时间与划分数组是否对称有关。如果划分是对称，从渐近意义上讲，与合并排序一样快，否则就与插入排序一样慢。

最坏情况为划分一个n-1个元素的子数组和一个0个元素的子数组。（最大程度不对称）。划分运行时间为Θ(n)。如果对一个0个元素的数组进行递归调用，运行时间为Θ(1).

递归式为：T(n) = T(n-1) + T(0) + Θ(n) = T(n-1) + Θ(n)。通过代换法可证明T(n) = Θ(n^2) （练习7.2-1）

证明：先假设C₁(n-1)^2 <= T(n-1) <= C₂(n-1)^2成立

　　　则C₁(n-1)^2 + Θ(n) <= T(n-1) + Θ(n) <= C₂(n-1)^2 + Θ(n)

　　　C₁n^2 -C₁(2n - 1) + Θ(n) <= T(n-1) + Θ(n) <= C₂n^2 -C₂(2n - 1) +  Θ(n)

　　　我们可以选择合适的常数C₁、C₂使得C₁(2n - 1)、C₂(2n - 1)支配Θ(n)。因此可以得出T(n) = Θ(n^2)。

注意，当输入数组完全排好序（升降序一样）和所有元素都是相同的值时，运行时间为Θ(n^2)，因为每次划分都是最大程度不对称。画画图，过一遍就会知道。

最佳情况为划分的两个子数组大小为floor(n/2)和ceiling(n/2)-1。

递归式为：T(n) <= 2T(n/2) + Θ(n)。该递归式的解为：T(n) = O(nlgn)

直接通过主定理的情况2得出。

平均情况运行时间更接近最佳情况而不是最坏情况。任一种按常数进行划分都会产生深度为Θ(lgn）的递归书，每一层的总代价为O(n)，因此运行时间为O(nlgn)。

从下图看可以更加明显

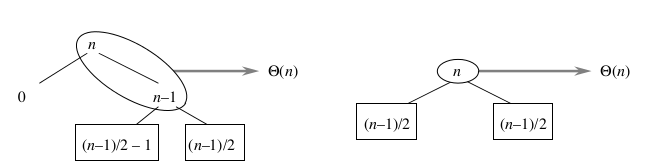
最坏情况的划分之后最佳情况划分的总代价与直接最佳情况的总代价都为Θ(n)。

练习7.2-5

假设快速排序的每一层，所做划分比例都是1-a：a，其中0<a<=1/2是个常数。证明：在对应的递归树中，叶结点的最小深度大约是-lgn/lga，最大深度大约是-lgn/lg(1-a)。

最小深度为每次划分后都是选择最小的一部分继续往下走，每次乘以a。一次迭代减少的元素数从n到an，迭代m次直到剩下的元素为1。

则(a^m)*n = 1， a^m = 1/n，取对数得mlga = -lgn，m = -lgn/lga。

同理可得((1-a)^M)*n = 1，M = -lgn/lg(1-a)。

快速排序随机化版本

便于对于所有输入，均能获得较好的平均情况性能。

/*
* 调用划分函数，使得子数组顺序重排
*/
void quick_sort(int A[], int p, int r){
if(p < r){
int q = partition(A, p, r);
quick_sort(A, p, q-1);
quick_sort(A, q+1, r);
}
}

/*
* 对于比x值小的元素通过交换放置到小于x值的区域。
* 最后将大于x值的区域的第一个元素与x值，即原A[r]，交换
* 该下标即为q，形成两个符合要求的数组（A[p..q-1]的元素都不大于A[q]，A[q+1..r]都不小于A[q]）
*/
int partition(int A[], int p, int r){
int x = A[r];
int i = p - 1;
int j;
for(j = p; j <= r-1; j++){
if(A[j] <= x){
i++;
int temp = A[i];
A[i] = A[j];
A[j] = temp;
}
}
int temp = A[i+1];
A[i+1] = A[r];
A[r] = temp;
return i+1;
}

 1 int randomized_partition(int A[], int p, int r){
 2     int i = p + rand() % (r - p + 1);
 3     int temp = A[r];
 4     A[r] = A[i];
 5     A[i] = temp;
 6     return partition(A, p, r);
 7 }
 8 
 9 int partition(int A[], int p, int r){
10     int x = A[r];
11     int i = p - 1;
12     int j;
13     for(j = p; j <= r-1; j++){
14         if(A[j] <= x){
15             i++;
16             int temp = A[i];
17             A[i] = A[j];
18             A[j] = temp;
19         }
20     }
21     int temp = A[i+1];
22     A[i+1] = A[r];
23     A[r] = temp;
24     return i+1;
25 }
26 
27 void randomized_quick_sort(int A[], int p, int r){
28     if(p < r){
29         int q = randomized_partition(A, p, r);
30         randomized_quick_sort(A, p, q-1);
31         randomized_quick_sort(A, q+1, r);
32     }
33 }

练习7.3-2

在randomized-quicksort的运行过程中，最坏情况下对随机数产生器random调用了多少次？最佳情况调用了多少次？

都为Θ(n)。

快速排序的分析

算导关于快排分析得很详细，数学太差了，看了很多遍才明白一点点，日后一定要继续努力，争取用自己的语言表达出来。

练习7.4-2

证明：快速排序的最佳情况运行时间为Ω(nlgn)

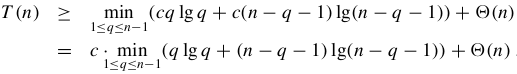
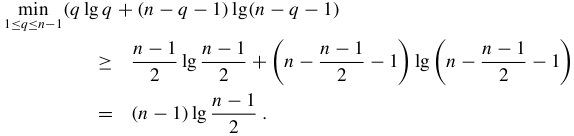
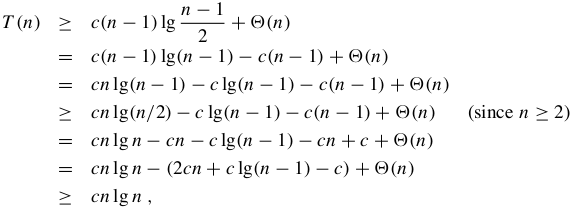
Hoare划分快速排序

划分方式有些不一样；前面的partition划分是将主元值与围绕它划分形成的两部分分隔开来。而Hoare划分则总是将主元值放入到两个划分的子数组里。

int hoare_partition(int A[], int p, int r){
int x = A[p];
int i = p;
int j = r;

while(i < j){
while(i < j && A[j] > x)
j--;
A[i] = A[j];
while(i < j && A[i] < x)
i++;
A[j] = A[i];
}
A[i] = x;
return j;
}

void hoare_quick_sort(int A[], int p, int r){
if(p < r){
int q = hoare_partition(A, p, r);
hoare_quick_sort(A, p, q-1);
hoare_quick_sort(A, q+1, r);
}
}

 1 int hoare_partition(int A[], int p, int r){
 2     int x = A[p];
 3     int i = p;
 4     int j = r;
 5 
 6     while(i < j){
 7         while(i < j && A[j] > x)
 8             j--;
 9         A[i] = A[j];
10         while(i < j && A[i] < x)
11             i++;
12         A[j] = A[i];
13     }
14     A[i] = x;
15     return j;
16 }
17 
18 void hoare_quick_sort(int A[], int p, int r){
19     if(p < r){
20         int q = hoare_partition(A, p, r);
21         hoare_quick_sort(A, p, q-1);
22         hoare_quick_sort(A, q+1, r);
23     }
24 }

继续努力。。。

Web页面性能测试工具浅析

Posted on 2013-09-28 17:56 fo0ol 阅读(277) 评论(4) 编辑 收藏

做Web开发，难免要对自己开发的页面进行性能检测，自己写工具检测，工作量太大。网上有几款比较成熟的检测工具，以下就介绍一下，与大家分享。

互联网现有工具

基于网页分析工具：

1.       阿里测

2.　　 百度应用性能检测中心

2.       Web PageTest

3.       PingDom Tools

4.       GTmetrix

基于浏览器分析工具：

1.       Chrome自带工具F12

2.       Firefox插件：YSlow（Yahoo工具）

3.       Page Speed（google）

（以下以分析博客园网站为例www.cnblogs.com）

阿里测：

http://www.alibench.com

 首页：

一、性能打分

a)         首字节时间

指标解释：浏览器开始收到服务器响应数据的时间(后台处理时间+重定向时间)
评估方法：达标时间=DNS解析时间+创建连接时间+SSL认证时间+100ms. 比达标时间每慢10ms减1分.

b)         使用长连接（keep alive）

指标解释： 服务器开启长连接后针对同一域名的多个页面元素将会复用同一下载连接(socket)
评估方法：服务器是否返回了"Connection: keep-alive"HTTP响应头,或者浏览器通过同一连接下载了多个对象

c)         开启GZIP压缩

指标解释：仅检查文本类型("text/*","*javascript*")
评估方法：服务器是否返回了"Transfer-encoding: gzip"响应头。假如全部压缩就是满分，否则:得分=满分x(100%-全部gzip后节省的比例%)

d)         图片压缩

评估方法：
对于GIF - 略过
对于PNG - 必须是8位或更低
对于JPEG - 对比使用photoshop质量选择50后的图片,尺寸超出10%以内及格,10%-50%警告,50%以上不达标
得分=满分x(100%-图片重新压缩后可以节省的比例%)

e)         设置静态内容缓存时间

指标解释：css,js,图片资源都应该明确的指定一个缓存时间
评估标准：如果有静态文件的过期时间设置小于30天，将会得到警告

f)          合并css和js文件

指标解释：合并js和css文件可以减少连接数
评估方法：每多一个css文件减5分，每多一个js文件减10分

g)         压缩JS

指标解释：除了开启gzip,使用js压缩工具可以进行代码级的压缩
评估方法：js文件会通过jsmin压缩.如果原始文件gzip过,jsmin处理过的文件也会gzip后再进行对比.如果能节省>5KB或者%10的尺寸,评估失败.如果能节省>1KB同样会收到警告.

h)         合理使用cookie

指标解释：cookie越小越好,而且对于静态文件需要避免设置cookie
评估方法：只要对静态文件域设置了cookie，评估失败. 对于其他请求，cookie尺寸过大会得到警告.

二、详情分析

i)           首次探测（首次探测会清空DNS缓存和浏览器缓存），重复探测（保留首次探测的缓存，进行再次探测）。

j)           页面加载时间：从页面开始加载到页面onload事件触发的时间。

k)         首字节时间：从开始加载到收到服务器返回数据的第一字节的时间。

l)           开始渲染时间：从开始加载到浏览器开始渲染第一个html元素的时间。

m)       Speed index：

n)         元素个数：页面中包含的所有DOM节点个数

o)         页面加载（包括加载时间，请求数，下载总计）：从页面开始加载到onload事件触发这个时间段内的统计数据，一般来说onload触发代表着直接通过HTML引用的CSS，JS，图片资源已经完全加载完毕。

p)         完全加载：随着ajax应用的流行，很多资源都会通过JS脚步异步加载，所以onload事件并不意味着完全加载，onload之后js可能依然在异步加载资源。完全加载的定义是：页面onload后2秒内不再有网络请求时刻。

q)         元素瀑布图：通过元素瀑布图可以很直观得到以下信息。

                         i.              资源的加载顺序。

                       ii.              每个资源的排队延迟，加载过程。

                      iii.              加载过程中CPU和贷款的变化曲线。

                      iv.              统计出出错请求、大图片请求、onload之后的请求、开始渲染之前的请求、首字节较慢的请求及DNS解析较慢的请求个数。

r)          连接视图展现了页面加载过程中创建的（keep-alive）连接，以及通过每个连接所加载的资源。

三、元素分布

s)         资源类型统计：css，html，image，js，other（请求数，大小）

t)          资源域名统计：请求域名个数及次数

四、视图分析

将整个网页生成的过程以胶片视图、视频、截屏的形式展现出来，并提供详细的状态栏加载日志。   

YSlow：

 火狐插件（自行安装）

评分等级指标：

1.       确保少量的HTTP请求（合并JS，CSS图片等）

2.       使用内容分发CDN

3.       设置过期的HTTP Header.设置Expires Header可以将脚本, 样式表, 图片, Flash等缓存在浏览器的Cache中。

4.       使用gzip压缩

5.       将CSS放置html头部

6.       将JavaScript放置底部

7.       Avoid CSS expressions

8.       使用外部引用JavaScript与CSS

9.       减少DNS解析

10.   压缩JavaScript和CSS

11.   避免URL重定向。URL redirects are made using HTTP status codes 301 and 302. They tell the browser to go to another location.

12.   删除重复JavaScript和CSS

13.   设置ETags

以上只是粗略介绍，更多详细指标，小伙伴们还是自己去发现吧！

 

 

 

标签: web, 性能, 前端

 

 

分类: 算法导论

标签: 算法导论