statpot:使用mongo+bootstrap+highcharts做统计报表
最近做了一个统计项目,这个统计项目大致的需求是统计接口的访问速度。客户端会调用一个接口来记录接口的访问情况,我的需求就需要分析这些数据,然后做出个统计报表。
需求实现
最初的时候想着每天把这些接口访问情况的信息存储到mysql中,然后根据这些访问情况做个分析再做报表。然后第一个问题就来了,信息包含太多字段了,如果我将每个信息解析成mysql表的一个字段,那么这个字段很长,而且还有一个致命缺陷,不容易扩展。如果将所有字段都存储为一个json,然后存储到text字段呢,又没法建立索引了。所以这种情况,最适合搬出mongo来了。
相比于mysql,mongo的好处就是扩展性好,灵活。像统计数据这样很容易需求不确定的数据确实是个很好的选择。我另外想想还有个好处就是不用的数据我可以很方便地将数据json化,然后存为文件。然后在需要的时候,也很容易读取直接放入到mongo中去。比如我可以将一个月的数据做一个持久备份之类的操作。
接着是生成统计报表的部分。各种图是很需要的,由于是给内部做统计报表,不需要兼顾各种浏览器。所以我选择了强大的highCharts。highCharts是一个JS图表库。很方便的就可以生成图表了。亲身体会是这个比flash做图表开发时间缩短多了。你可以从http://www.highcharts.com/上下载3.0版本。
后续呢,由于后面有很多统计变化的需求。每次都写一个过程来生成js代码从而渲染统计报表也是个很繁琐的事情。于是我就打算写一个工具,大致的思路就是依靠修改配置文件就可以直接生成统计报表,报表的页面为了美观我引入了bootstrap 3.0。于是发现这种数据存储mongo,加上配置文件生成报表的模式是很容易实现,也确实很好使用。甚至于你在mongo中增加了一种统计结构,我可以什么都不用修改,只需要增加一个配置项就可以生成新统计结构的图表了,这大都是归功于mongo的json结构化。
statpot工具
这个工具statpot开源在github上了:
https://github.com/jianfengye/statpot
可以下载result/stat_20130925.html来看生成的报表。
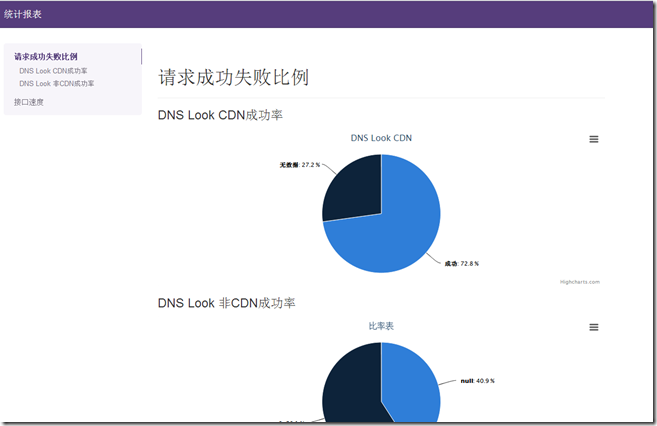
生成的报表如下:
现在是实现了两种:饼图和柱状图。后续有可能的话还会继续加上一些其他统计图表。
还能想到的一个问题是这个页面如果是动态的,那么必然实时分析需要的时间比较多,而统计报表一般不需要动态的,所以完全可以做成生成静态文件的方式,于是web/目录下就有动态和静态的入口。这种生成静态报表然后存储的方式也是很好的,比如每天我生成一次动态报表,然后就把mongo中的数据清空或这静态文件化。
当然后来想想,这种唯配置至上的工具唯一的弊端是配置本身就是一种学习成本,你需要花时间来掌握这个配置。但是这个问题在我看来,和代码一样,应该由配置的语义来解决。
问题记录
记录下开发过程中特别是使用mongo中遇到的问题:
如何获取一个字段的所有可能的值
使用distinct
如何获取一个字段的所有可能的值,并且计算出每个值有多少个条目
需要使用group命令
group的命令文档在:http://docs.mongodb.org/manual/reference/method/db.collection.group/
> db.feedbacks.group({
"key" : {"keys.properties.network_type": true},
"initial":{"count":0},
"$reduce":function(cur,prev){
prev.count=prev.count+1;
}
})
对应的PHP mongo的API是:http://www.php.net/manual/zh/mongocollection.group.php
参考文章
http://www.cnblogs.com/huangxincheng/archive/2012/02/21/2361205.html
http://api.highcharts.com/highcharts
http://docs.mongodb.org/ecosystem/drivers/php/
javascript面向对象的写法01
类和对象
js中内置有对象的概念。下面是对象创建的一些方式。
1 var obj = new Object(); 2 obj.a = 1; 3 obj.func1 = function(){};
另外有两种创建对象的方式
1 var obj = {}; 2 function ClassA() { 3 }
第一种是js的字典,字典本身也是一个js对象。因为动态语言的特性它可以存放各种类型的数据,包括函数指针
1 var obj = { 2 "attr1": 1, 3 "attr2": [], 4 "fun1": function(a, b) { 5 return a + b; 6 } 7 };
1 var a = obj.attr1; 2 var b = obj.fun1(1, 6); 3 obj.attr1 = 9; 4 var c = obj.attr1;
这样字典对象本身的使用语法跟其他语言类也是相似的。它可以看作一个简单的对象使用。它与第一种方式差不多,是第一种的替代方案。
function的作用
function func1(a, b) { return a + b; } func1(1, 2);
function A() { } A.a = 100; alert(A.a);
function A() { } var obj = new A(); obj.attr = 100;
它可是被看成是对象的构造函数
function A(a, b) { this.a = a; this.b = b; } var obj = new A(); obj.a;
this指向的是当前对象的引用,这个和其他语言类似。上例代码相当于
function A() { } var obj = new A(); obj.a = a; obj.b = b;
(注:这个简单的转换对后续的内容的理解有所帮助)
1 function ClassA() { 2 this.a = 1; 3 this.b = []; 4 this.func1 = function() { 5 return this.a + 100; 6 }; 7 }
使用的时候使用new关键字,new出一个对象来
1 var objA = new ClassA(); 2 var a = objA.a; 3 var b = objA.func1(); 4 objA.a = 200;
上面定义类的方式可以看成如下
1 function ClassA() { 2 } 3 4 //js是动态语言,js对象的属性不需要定义对象的时候写好,而是可以在任意时候设置,这是动态语言的特点。 5 var objA = new ClassA(); 6 objA.a = 1; 7 objA.b = []; 8 objA.func1 = function(){return this.a + 100};
红黑树并没有我们想象的那么难(上)
2013-09-26 11:01 by 捣乱小子, 909 阅读, 12 评论, 收藏, 编辑
红黑树并没有想象的那么难, 初学者觉得晦涩难读可能是因为情况太多. 红黑树的情况可以通过归结, 通过合并来得到更少的情况, 如此可以加深对红黑树的理解. 网络上的大部分红黑树的讲解因为没有「合并」. 红黑树的五个性质:
性质1. 节点是红色或黑色。
性质2. 根是黑色。
性质3. 所有叶子都是黑色(叶子是NIL节点)。
性质4. 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
性质5. 从任一节点到其每个叶子的所有简单路径 都包含相同数目的黑色节点。
红黑树的数据结构
摘自 sgi stl 红黑树数据结构定义:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
typedef bool _Rb_tree_Color_type;const _Rb_tree_Color_type _S_rb_tree_red = false;const _Rb_tree_Color_type _S_rb_tree_black = true;struct _Rb_tree_node_base{ typedef _Rb_tree_Color_type _Color_type; typedef _Rb_tree_node_base* _Base_ptr; _Color_type _M_color; _Base_ptr _M_parent; _Base_ptr _M_left; _Base_ptr _M_right; static _Base_ptr _S_minimum(_Base_ptr __x) { while (__x->_M_left != 0) __x = __x->_M_left; return __x; } static _Base_ptr _S_maximum(_Base_ptr __x) { while (__x->_M_right != 0) __x = __x->_M_right; return __x; }};template <class _Value>struct _Rb_tree_node : public _Rb_tree_node_base{ typedef _Rb_tree_node<_Value>* _Link_type; _Value _M_value_field;}; |
二叉搜索树的插入删除操作
在展开红黑树之前, 首先来看看普通二叉搜索树的插入和删除. 插入很容易理解, 比当前值大就往右走, 比当前值小就往左走. 详细展开的是删除操作.
二叉树的删除操作有一个技巧, 即在查找到需要删除的节点 X; 接着我们找到要么在它的左子树中的最大元素节点 M、要么在它的右子树中的最小元素节点 M, 并交换(M,X). 此时, M 节点必然至多只有一个孩子; 最后一个步骤就是用 M 的子节点代替 M 节点就完成了. 所以, 所有的删除操作最后都会归结为删除一个至多只有一个孩子的节点, 而我们删除这个节点后, 用它的孩子替换就好了. 将会看到 sgi stl map 就是这样的策略.
在红黑树删除操作讲解中, 我们假设代替 M 的节点是 N(下面的讲述不再出现 M).
红黑树的插入
插入新节点总是红色节点, 因为不会破坏性质 5, 尽可能维持所有性质.
假设, 新插入的节点为 N, N 节点的父节点为 P, P 的兄弟(N 的叔父)节点为 U, P 的父亲(N 的爷爷)节点为 G. 所以有如下的印象图:
插入节点的关键是:
- 插入新节点总是红色节点
- 如果插入节点的父节点是黑色, 能维持性质
- 如果插入节点的父节点是红色, 破坏了性质. 故插入算法就是通过重新着色或旋转, 来维持性质
插入算法详解如下, 走一遍红黑树维持其性质的过程:
第 0.0 种情况, N 为根节点, 直接 N->黑. over
第 0.1 种情况, N 的父节点为黑色, 这不违反红黑树的五种性质. over
第 1 种情况, N,P,U 都红(G 肯定黑). 策略: G->红, N,P->黑. 此时, G 红, 如果 G 的父亲也是红, 性质又被破坏了, HACK: 可以将 GPUN 看成一个新的红色 N 节点, 如此递归调整下去; 特俗的, 如果碰巧将根节点染成了红色, 可以在算法的最后强制 root->红.
第 2 种情况, P 为红, N 为 P 右孩子, N 为红, U 为黑或缺少. 策略: 旋转变换, 从而进入下一种情况:
第 3 种情况, 可能由第二种变化而来, 但不是一定: P 为红, N 为 P 左孩子, N 为红. 策略: 旋转, 交换 P,G 颜色, 调整后, 因为 P 为黑色, 所以不怕 P 的父节点是红色的情况. over
红黑树的插入就为上面的三种情况. 你可以做镜像变换从而得到其他的情况.
红黑树的删除
假设 N 节点见上面普通二叉树删除中的定义, P 为 N 父节点, S 为 N 的兄弟节点, SL,SR 分别是 S 的左右子节点. 有如下印象图:
删除节点的关键是:
- 如果删除的是红色节点, 不破坏性质
- 如果删除的是黑色节点, 那么这个路径上就会少一个黑色节点, 破坏了性质. 故删除算法就是通过重新着色或旋转, 来维持性质
删除算法详解如下, 走一遍红黑树维持其性质的过程:
第 0.0 情况, N 为根节点. over
第 0.1 情况, 删除的节点为红. over
第 0.2 情况, 删除节点为黑, N 为红. 策略: N->黑, 重新平衡. over
第 1 情况, N,P,S,SR,SL 都黑. 策略: S->红. 通过 PN,PS 的黑色节点数量相同了, 但会比其他路径多一个, 解决的方法是在 P 上从情况 0 开始继续调整. 为什么要这样呢? HANKS: 因为既然 PN,PS 路径上的黑节点数量相同而且比其他路径会少一个黑节点, 那何不将其整体看成了一个 N 节点! 这是递归原理.
第 2 情况, S 红, 根据红黑树性质 P,SL,SR 一定黑. 策略: 旋转, 交换 P,S 颜色. 处理后关注的范围缩小, 下面的情况对应下面的框图, 算法从框图重新开始, 进入下一个情况:
第 2.1 情况, S,SL,SR 都黑. 策略: P->黑. S->红, 因为通过 N 的路径多了一个黑节点, 通过 S 的黑节点个数不变, 所以维持了性质 5. over. 将看到, sgi stl map 源代码中将第 2.1 和第 1 情况合并成一种情况, 下节展开.
第 2.2.1 情况, S,SR 黑, SL 红. 策略: 旋转, 变换 SL,S 颜色. 从而又进入下一种情况:

第 2.2.2 情况, S 黑, SR 红. 策略: 旋转, 交换 S,P 颜色, SR->黑色, 重新获得平衡.
上面情况标号 X.X.X 并不是说这些关系是嵌套的, 只是这样展开容易理解. 此时, 解释三个地方:
- 通过 N 的黑色节点数量多了一个
- 通过 SL 的黑色节点数量不变
- 通过 SR 的黑色节点数量不变
红黑树删除重新调整伪代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
// 第 0.0 情况, N 为根节点. overif N.parent == NULL: return;// 第 0.1 情况, 删除的节点为红. overif color == RED: return;// 第 0.2 情况, 删除节点为黑, N 为红, 简单变换: N->黑, 重新平衡. overif color == BLACK && N.color == RED: N.color = BLACK;// 第 1 种情况, N,P,S,SR,SL 都黑. 策略: S->红. 通过 N,S 的黑色节点数量相同了, 但会比其他路径多一个, 解决的方法是在 P 上从情况 0 开始继续调整.if N,P,S,SR,SL.color == BLACK: S.color = RED; // 调整节点关系 N = P N.parent = P.parent S = P.paernt.another_child SL = S.left_child SR = S.right_child continue;// 第 2 情况, S 红, 根据红黑树性质 P,SR,SL 一定黑. 旋转, 交换 P,S 颜色. 此时关注的范围缩小, 下面的情况对应下面的框图, 算法从框图重新开始.if S.color == RED: rotate(P); swap(P.color,S.color); // 调整节点关系 S = P.another_child SL = S.left_child SR = S.right_child// 第 2.1 情况, S,SL,SR 都黑. 策略: P->黑. S->红, 因为通过 N 的路径多了一个黑节点, 通过 S 的黑节点个数不变, 所以维持了性质 5. overif S,SL,SR.color == BLACK: P.color = BLACK; S.color = RED; return// 第 2.2.1 情况, S,SR 黑, SL 红. 策略: 旋转, 变换 SL,S 颜色. 从而又进入下一种情况:if S,SR.color == BLACK && SL.color == RED: rotate(P); swap(S.color,SL.color); // 调整节点关系 S = SL SL = S.left_child SR = S.right_child// 第 2.2.2 情况, S 黑, SR 红. 策略: 旋转, 交换 S,P 颜色.if S.color == BLACK && SR.color == RED: rotate(P); swap(P.color,S.color); return; |
总结
所以, 插入的情况只有三种, 删除的情况只有两种. 上面的分析, 做镜像处理, 就能得到插入删除的全部算法, 脑补吧. 从上面的分析来看, 红黑树具有以下特性: 插入删除操作都是 0(lnN), 且最多旋转三次.
下节中会重点展开 sgi stl map 的源代码.
参考文档: wikipedia
捣乱 2013-9-25