《算法导论》第六章----堆排序
堆数据结构是一种数组对象，它可以被视为一棵完全二叉树。
二叉堆有两种：最大堆和最小堆。
最大堆的特性是指除了根以外每个节点的值最多和其父节点的值一样大。
堆可以被看成是一棵树，其高度为
。（练习证明稍后上）
保持堆的性质
1 /* 2 *这个函数是维持堆的性质，注意当调用这个函数的时候，我们假定该节点的左右儿子树都是最大堆。 3 *但是有可能该节点小于它的子树，所以通过这个函数使该节点下降，使以该节点为根的子树成为最大堆。 4 */ 5 void max_heapify(int A[], int length, int i){ 6 int l = 2 * i; //左儿子节点下标 7 int r = 2 * i + 1; //右儿子节点下标 8 int largest; //记录该节点与左右儿子节点中值最大的下标 9 10 if(l <= length && A[l] > A[i]) 11 largest = l; 12 else 13 largest = i; 14 15 if(r <= length && A[r] > A[largest]) 16 largest = r; 17 18 if(largest != i){ 19 int temp = A[largest]; 20 A[largest] = A[i]; 21 A[i] = temp; 22 max_heapify(A, length, largest); 23 } 24 }
过程如下图
函数作用与一棵以节点i为根的、大小为n的子树上时，调整节点i与其儿子的关系时，所用时间为
，再加上对以i的某个子节点为根的子树调用维持堆的性质的函数所需时间为：
T(n) <= T(2n/3) + （最坏情况为最底层恰好半满）（PS：why is 2n/3? 第一层都倒数第二层节点个数为：1、2、4.......2^x、2^x。2^x / (2^(x-1) + 2^x + 2^x) = 2n/3）
根据主定理（维基）的情况二，递归式的解为T(n) = 
建堆
1 /* 2 *练习6.3-2：为什么从下标floor(length/2)降到1，而不是从1升到floor(legnth/2)? 3 *max_heapify函数假设左右儿子为根的二叉树都为最大堆，如果从1开始的话，其左右儿子为根的二叉树不一定为最大堆。 4 *而从floor(length/2)开始则可以保证左右儿子为根的二叉树都是最大堆 5 */ 6 void build_max_heap(int A[], int length){ 7 int i; 8 for(i = length/2; i >= 1; i--) 9 max_heapify(A, length, i); //调用维持最大堆的性质函数 10 }
过程如下图：
这个函数的上界可以为O(n * lgn)。O(n)次调用维持最大堆的性质函数（O(lgn)）。但是不是每个节点调用这个函数所需的时间一致。
一个n元素的堆的高度为floor(lgn)，在任意高度h上，最多有ceiling(n/2^(h+1))个节点（PS：证明稍候上）
然后直接上具体证明运行时间界O(n)（PS：本人数学不是很好。。。。）
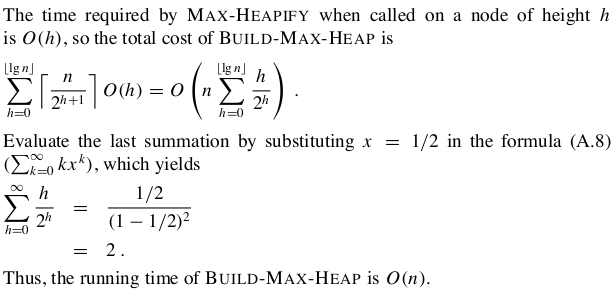
堆排序算法
/* *数组A[1...n]的最大元素为A[1],通过与A[n]交换达到最终正确的位置。原来根的子女依然是最大堆， *但是新的根元素可能违背最大堆的性质。因此要调用维持最大堆性质的函数 *然后在A[1...n-1]里重复这个过程。 */ void heap_sort(int A[], int length){ int i; int size = length; build_max_heap(A, length); //建堆 for(i = length; i >= 2; i--){ int temp = A[i]; A[i] = A[1]; A[1] = temp; //交换，将最大的元素放到数组的还没排序的尾部。 size--; max_heapify(A, size, 1); //调用维持最大堆的性质的函数（此时根节点的左右儿子子树为最大堆） } }
过程如下图：
该过程的时间代价为O(n * lgn)，调用建堆的时间为O(n)，n-1次调用维持最大堆的性质（O(lgn)）
堆排序
#include <stdio.h>
#include <stdlib.h>
/*
int parent(int i); //返回父节点下标
int left(int i); //返回左儿子节点下标
int right(int i); //返回右儿子节点下标
*/
void max_heapify(int A[], int length, int i); //保持堆的性质
void build_max_heap(int A[], int length); //在输入数组基础上构造出最大堆
void heap_sort(int A[], int length); //对一个数组原地进行排序
int main(){
int num, i;
printf("Input the number:
");
scanf("%d", &num);
int *array = malloc((num + 1) * sizeof(int));
printf("Input the element:");
for(i = 1; i <= num; i++)
scanf("%d", &array[i]);
heap_sort(array, num);
for(i = 1; i <= num; i++)
printf("%d ", array[i]);
printf("
");
return 0;
}
/*
*这个函数是维持堆的性质，注意当调用这个函数的时候，我们假定该节点的左右儿子树都是最大堆。
*但是有可能该节点小于它的子树，所以通过这个函数使该节点下降，使以该节点为根的子树成为最大堆。
*/
void max_heapify(int A[], int length, int i){
int l = 2 * i; //左儿子节点下标
int r = 2 * i + 1; //右儿子节点下标
int largest; //记录该节点与左右儿子节点中值最大的下标
if(l <= length && A[l] > A[i])
largest = l;
else
largest = i;
if(r <= length && A[r] > A[largest])
largest = r;
if(largest != i){
int temp = A[largest];
A[largest] = A[i];
A[i] = temp;
max_heapify(A, length, largest);
}
}
/*
*练习6.3-2：为什么从下标floor(length/2)降到1，而不是从1升到floor(legnth/2)?
*max_heapify函数假设左右儿子为根的二叉树都为最大堆，如果从1开始的话，其左右儿子为根的二叉树不一定为最大堆。
*而从floor(length/2)开始则可以保证左右儿子为根的二叉树都是最大堆
*/
void build_max_heap(int A[], int length){
int i;
for(i = length/2; i >= 1; i--)
max_heapify(A, length, i); //调用维持最大堆的性质函数
}
/*
*数组A[1...n]的最大元素为A[1],通过与A[n]交换达到最终正确的位置。原来根的子女依然是最大堆，
*但是新的根元素可能违背最大堆的性质。因此要调用维持最大堆性质的函数
*然后在A[1...n-1]里重复这个过程。
*/
void heap_sort(int A[], int length){
int i;
int size = length;
build_max_heap(A, length); //建堆
for(i = length; i >= 2; i--){
int temp = A[i];
A[i] = A[1];
A[1] = temp; //交换，将最大的元素放到数组的还没排序的尾部。
size--;
max_heapify(A, size, 1); //调用维持最大堆的性质的函数（此时根节点的左右儿子子树为最大堆）
}
}
堆排序