数据结构之栈(Stack)与队列(Queue)
(本文为个人学习数据结构课程和三年磨一剑的<<大话数据结构>> 后的笔记,如有侵权,请直接联系我,立即删除)(杯具了,昨天写的保存的时候,着急了没看,早上来看没有发布成果,只有从头再写一遍了)
一.栈(Stack)
1.定义:仅在表尾进行插入和删除操作的线性表
2.栈的抽象数据类型:
ADT 栈(Stack)
Data
同线性表.元素具有相同的类型,相邻元素具有前驱和后继关系.
Operation
InitStack(*S): 初始化操作,建立一个空的栈.
DestoryStack(*S): 若栈存在,则销毁它.
StackEmpty(S): 若线栈为空,返回true,否则返回false.
CleaStack(*L): 将栈清空.
GetTop(L,i,*e): 若栈不为空,用e返回栈顶元素.
Push(*S,e): 若栈存在,置插入新元素e到栈S中并成为栈顶元素.
Pop(*S,*e): 若栈不为空,删除栈的栈顶元素,并用e返回其值.
StackLentgth(L) : 返回栈S的元素个数.
3.栈的顺序存储结构


运行结果:
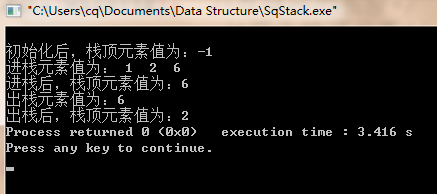
4.栈的链式存储结构

运行结果:

5.栈的应用
1).递归
菲波那契(Fibonacci)数列
0 , 当n =0
F(n) = 1 , 当n=1
F(n-1)+F(n-2) , 当n>1
迭代:
递归:
通过分析递归时的执行的退回顺序是它前行顺序的逆序
2).四则运算表达式求值
中缀表达式(标准四则运算表达式),即"9+ (3-1) X3+10/2"叫作中缀表达式.
中缀表达式转后缀表达式:
规则: 从左到右遍历表达式的每个数字和符号,遇到数字就输出,即成为后缀表达式的一部分,遇到符号,就先判断其与栈顶符号的优先级,是右括号或优先级低的于
栈顶符号(乘除优先加减)则栈顶依次出栈并输出,并将当前符号进栈,一直到输出后缀表达式为止.
中缀表达式:"9+ (3-1) X3+10/2"
步骤:
1.初始化一个空栈,用来对符号进出使用
2.第一个字符是数字9,将9输出,后面是"+",进栈.
3.第三个字符"(",因其是左括号,还未匹配,故进栈,后面是数字3,输出3,总表达式为93,接着是"-",进栈.
4.接下来是数字1,输出,总表达式为:931,后面是符号")",此时,匹配此前的"(",所以栈顶元素依次出栈,并输出,直到"("出栈为止.输出"-",此时总表达式为:931-
5.接下来是"*",优先级高于"+","*"进栈,接着是数字3,输出,此时从表达式为931-3.
6.之后是"+",比此时栈顶符号为"*"的优先级低,栈中元素出栈并输出(没有比"+"号更低的优先级,所以全部出栈),总输出表达式为:931-3*-.然后激昂当前"+"进栈
7.紧接着是10,输出,后是符号"/",优先级高于"+",进栈,最后一个是数字2输出.此时总表达式为931-3*+10 2
8.已经到了最后,栈中符号依次出栈并输出,最终输出表达式为:"9 3 1 - 3 * + 10 2 / 4"
后缀表达式(逆波兰表示):一种不需要括号的后缀表达式,上中缀表达式转化为后缀表达式为:"931-3*+102/+"
后缀表达式的运算:
规则:从左到右遍历表达式的每个数字和符号,遇到数字就进栈,遇到符号,就将处于栈顶的2个数字出栈,进行运算,运算结果进栈,
一直到最终获得结果.
后缀表达式:"931-3*+102/+"
步骤:
1.初始化一个空栈,用来对要运算数字进出使用.
2.后缀表达式中前三个都是数字,所以9,3,1进栈,此时栈中元素从上到下依次为1,3,9
3.接下来是"-",所以将栈中的1出栈作为减数,3出栈作为被除数,运算 "3-1=2", 将2进栈,再将后面一位数字3进栈,此时栈中元素从上到下依次为3,2,9
4.后面是"*",也就意味着栈中3和2出栈,2和3相乘,得到6,将6进栈,此时栈中元素从上到下依次为6,9
5.下面是"+",所以栈中6和9出栈,6+9=15,将15进栈,此时栈中只有一个元素15
6.接着就是10,2,依次进栈,此时栈中元素从上到下依次为2,10,15
7.接下来是符号"/",将2,10出栈,2为除数,10为被除数,10/2=5,将5进栈,此时栈中元素从上到下依次为5,15
8.最后一个符号"+",栈中最后2个元素出栈,相加得到20,为最终结果
二.队列(Queue)
1.定义:只允许在一端(队尾)进行插入操作,而在另一端(对头)进行删除操作.
2.队列的抽象数据类型:
ADT 队列(Queue)
Data
同线性表.元素具有相同的类型,相邻元素具有前驱和后继关系.
Operation
InitQueue(*Q): 初始化操作,建立一个空的队列Q.
DestoryQueue(*Q): 若队列存在,则销毁它.
CleaQueue(*Q): 将队列清空.
QueueEmpty(Q): 若线性表为空,返回true,否则返回false.
GetHead(Q,*e): 若队列存在且非空,用e返回队列Q的对头元素.
EnQueue(*Q,e): 若队列存在,新元素e到队列Q中并成为对尾元素.
DeQueue(*Q,*e): 若队列存在,删除队列中的头元素,并用e返回其值.
QueueLentgth(L) : 返回队列的元素个数.
3.队列的顺序存储结构


A. 1 B.2 C.3 4.D
循环队列:

运行结果:

4.队列的链式存储结构

运行结果:

农夫过河问题
一个农夫带着一只狼、一只羊和一棵白菜,身处河的南岸。他要把这些东西全部运到北岸。问题是他只有一条船,船小到只能容下他和一件物品,当然,船只有农夫能撑。另外,因为狼能吃羊,而羊爱吃白菜,所以农夫不能留下羊和狼或者羊和白菜单独在河的一边,自己离开。好在狼属于食肉动物,它不吃白菜。请问农夫该采取什么方案,才能将所有的东西安全运过河呢?
一、算法与数据结构的设计:
要模拟农夫过河的问题,用四位二进制数顺序分别表示农夫、狼、白菜和羊的位置。用0表示农夫和或者某种东西在河的南岸,1表示在河的北岸。则问题的初始状态是整数(其二进制表示为0000);而问题的终结状态是整数15(其二进制表示为1111)。
用整数location表示用上述方法描述的状态,函数返回值为真(1)表示所考察的人或物在河的北岸,否则在南岸。
二、算法的精化:
用一个整数队列moveTo,把搜索过程中每一步所有可能达到的状态都保存起来。队列中每一个元素表示一个可以安全到达的中间状态。另外,用一个整数数组route,用于记录已被访问过的各个状态,以及已被发现的能够到达这些状态的前驱状态。route数组只需要使用16个元素。Route的每一个元素初始化值均设置为-1,每当在队列加入一个新状态时,就把route中以该状态坐下标的元素的值改为达到这个状态的前一状态的下标值。所以,数组的第i个元素,不仅记录状态i是否已被访问过,同时对已被访问过的状态,还保存了这个状态的前驱状态下标。算法结束后,可以利用route数组元素的值生成一个正确的状态路径。
程序运行结果如下: The reverse path is :
The location is : 15
The location is : 6
The location is : 14
The location is : 2
The location is : 11
The location is : 1
The location is : 9
The location is : 0
结果分析:从初始状态0到最后状态15的动作序列为:
1.初始全部在南岸(0000),
2农夫把羊带到北岸(1001),
3.农夫独自回到南岸(0001),
4.农夫把白菜带到北岸(1011),
5.农夫带着羊回到南岸(0010),
6.农夫把狼带到北岸(1110),
7.农夫独自回到南岸(0110),
8.农夫把羊带到北岸(1111)
程序运行最后location结果为15(二进制为1111),
即农夫和其他东西都安全运过了北岸。解决了农夫过河问题.