冒泡排序介绍
冒泡排序是我们得最多的排序方式之一,原因是简单易实现,且原理易懂。顾名思义,冒泡排序,它的排序过程就像水中的气泡一样,一个一个上浮到水面。

冒泡排序原理分析
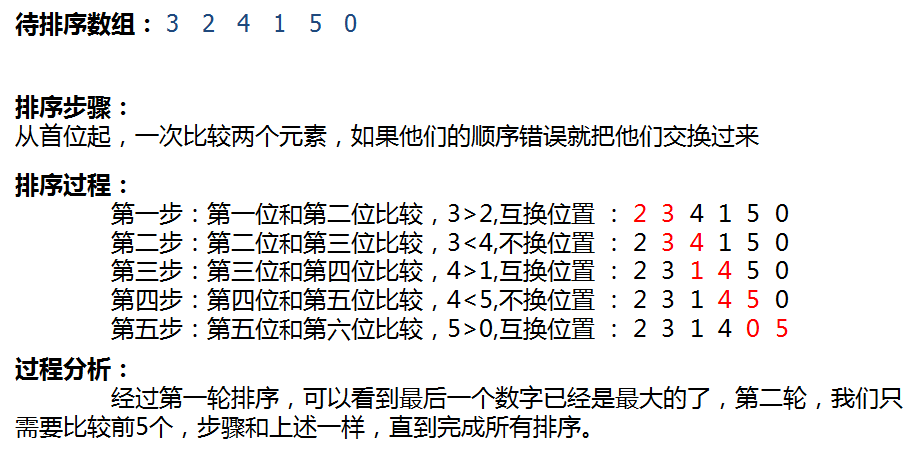
冒泡排序代码实现
/**
* @Author {LearnAndGet}
* @Time 2019年1月8日
* @Discription:
*/
package com.sort;
import java.util.Arrays;
public class MaopaoSort {
static int[] array = {3,2,4,1,5,0};
public static void maopaoSort(int[] a)
{
//外层循环,是需要进行比较的轮数,一共进行5次即可
for(int i=0;i<a.length-1;i++)
{
//内存循环,是每一轮中进行的两两比较
for(int j=0;j<a.length-1;j++)
{
if(a[j] > a[j+1])
{
int temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
}
}
System.out.println("第"+(i+1)+"轮排序后的数组为: "+Arrays.toString(a));
}
}
public static void main(String[] args) {
maopaoSort(array);
}
}
输出结果
第1轮排序后的数组为: [2, 3, 1, 4, 0, 5]
第2轮排序后的数组为: [2, 1, 3, 0, 4, 5]
第3轮排序后的数组为: [1, 2, 0, 3, 4, 5]
第4轮排序后的数组为: [1, 0, 2, 3, 4, 5]
第5轮排序后的数组为: [0, 1, 2, 3, 4, 5]
冒泡排序的优化
1 .观察上述代码和运行结果,我们可以发现,当第一轮结束后,最后一个数字一定是数组中最大的元素,那么我们在进行第二趟的两两比较时,实际上是没有必要再对第5个和第6个进行比较的。那么我们可以修改代码如下:
public static void maopaoSort(int[] a)
{
//外层循环,是需要进行比较的轮数,一共进行5次即可
for(int i=0;i<a.length-1;i++)
{
//内存循环,是每一轮中进行的两两比较
//并且每一轮结束后,下一次的两两比较中可以少比较一次
for(int j=0;j<a.length-i-1;j++)
{
if(a[j] > a[j+1])
{
int temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
}
}
System.out.println("第"+(i+1)+"轮排序后的数组为: "+Arrays.toString(a));
}
}
继续运行后,可以发现运行结果是一样的。
2 .当我们用数组:{1,2,0,3,5,4}来测试上述冒泡排序时,运行结果如下:
第1轮排序后的数组为: [1, 0, 2, 3, 4, 5]
第2轮排序后的数组为: [0, 1, 2, 3, 4, 5]
第3轮排序后的数组为: [0, 1, 2, 3, 4, 5]
第4轮排序后的数组为: [0, 1, 2, 3, 4, 5]
第5轮排序后的数组为: [0, 1, 2, 3, 4, 5]
可以看到,在第2轮排序完成后,其实我们就已经的到了排好序的数组,但是我们的程序并不知道,仍然进行了后续的无用工作。那么,我们如何来让程序知道已经完成好排序了呢?
这里可以想到,当某一轮的两两比较中,如果都没有发生数组元素的互换,那么其实排序工作已经完成了,所以我们可以考虑在程序中加入一个flag,默认为false,含义是该轮比较中是否发生了元素互换,当程序中执行到元素互换时,将该flag置为true,当该轮比较结束时,若flag为flase,则说明该轮比较未发生元素互换,那么排序完成,若flag为true,说明本轮比较仍然有元素互换,需要继续进行下轮排序。代码实现如下:
/**
* @Author {LearnAndGet}
* @Time 2019年1月8日
* @Discription:
*/
package com.sort;
import java.util.Arrays;
public class MaopaoSort {
static int[] array = {1,2,0,3,5,4};
public static void maopaoSort(int[] a)
{
//外层循环,是需要进行比较的轮数,一共进行5次即可
for(int i=0;i<a.length-1;i++)
{
boolean flag = false;
//内存循环,是每一轮中进行的两两比较
for(int j=0;j<a.length-i-1;j++)
{
if(a[j] > a[j+1])
{
int temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
flag = true;
}
}
System.out.println("第"+(i+1)+"轮排序后的数组为: "+Arrays.toString(a));
if(flag == false)
{
System.out.println("本轮中的两两比较未发生元素互换,排序已经完成啦");
return;
}
}
}
public static void main(String[] args) {
maopaoSort(array);
}
}
运行结果:
第1轮排序后的数组为: [1, 0, 2, 3, 4, 5]
第2轮排序后的数组为: [0, 1, 2, 3, 4, 5]
第3轮排序后的数组为: [0, 1, 2, 3, 4, 5]
本轮中的两两比较未发生元素互换,排序已经完成啦
冒泡排序的时间复杂度
冒泡排序是一种用时间换空间的排序方法,最坏情况是把顺序的排列变成逆序,或者把逆序的数列变成顺序。在这种情况下,每一次比较都需要进行交换运算。举个例子来说,一个数列 5 4 3 2 1 进行冒泡升序排列
第一轮的两两比较,需要比较4次;得到 4 3 2 1 5
第二轮的两两比较,需要比较3次;得到 3 2 1 4 5
第三轮的两两比较,需要比较2次;得到 2 1 3 4 5
第四轮的两两比较,需要比较1次;得到 1 2 3 4 5
所以总的比较次数为 4 + 3 + 2 + 1 = 10次
对于n位的数列则有比较次数为 (n-1) + (n-2) + ... + 1 = n * (n - 1) / 2,这就得到了最大的比较次数。
而O(N^2)表示的是复杂度的数量级。举个例子来说,如果n = 10000,那么 n(n-1)/2 = (n^2 - n) / 2 = (100000000 - 10000) / 2,相对10^8来说,10000小的可以忽略不计了,所以总计算次数约为0.5 * N2。用O(N2)就表示了其数量级(忽略前面系数0.5)。
综上所述,冒泡排序的时间复杂度为:O(n²)