[codeforces631E]Product Sum

E. Product Sum

time limit per test:

1 second

memory limit per test:

256 megabytes

input:standard input

output:standard output

Blake is the boss of Kris, however, this doesn't spoil their friendship. They often gather at the bar to talk about intriguing problems about maximising some values. This time the problem is really special.

You are given an array a of length n. The characteristic of this array is the value 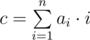 — the sum of the products of the valuesai by i. One may perform the following operation exactly once: pick some element of the array and move to any position. In particular, it's allowed to move the element to the beginning or to the end of the array. Also, it's allowed to put it back to the initial position. The goal is to get the array with the maximum possible value of characteristic.

Input

The first line of the input contains a single integer n (2 ≤ n ≤ 200 000) — the size of the array a.

The second line contains n integers ai (1 ≤ i ≤ n, |ai| ≤ 1 000 000) — the elements of the array a.

Output

Print a single integer — the maximum possible value of characteristic of a that can be obtained by performing no more than one move.

Examples

input

4
4 3 2 5

output

39

input

5
1 1 2 7 1

output

49

input

3
1 1 2

output

9

Note

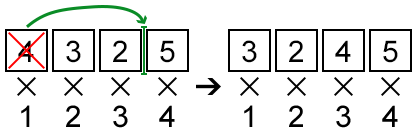
In the first sample, one may pick the first element and place it before the third (before 5). Thus, the answer will be3·1 + 2·2 + 4·3 + 5·4 = 39.

In the second sample, one may pick the fifth element of the array and place it before the third. The answer will be1·1 + 1·2 + 1·3 + 2·4 + 7·5 = 49.

题解:

刚看这个题我十分的懵逼,这怎么做?

于是我就想了个暴力O(n²)的算法:如果没有这个"exactly once"的移动,问题的答案很容易算出来,设为ans

而由于只能移动一次,所以我可以枚举移动的方案,看每种移动对答案的贡献,设为delta,选最大贡献,最终答案为ans+delta

scanf("%d",&n);
for(LL i=1;i<=n;i++)
{
    cin>>a[i];
    s[i]=a[i]+s[i-1];
    ans1+=a[i]*i;
}
for(int l=1;l<=n;l++)
    for(int r=l+1;r<=n;r++)
    {
        delta=max(delta,a[l]*(r-l)-(s[r]-s[l]));
        delta=max(delta,s[r-1]-s[l-1]-a[r]*(r-l));
    }
cout<<delta+ans1;

这样肯定会t,所以我们考虑一下刚才那个暴力的式子

"delta=max(delta,a[l]*(r-l)-(s[r]-s[l]));"

"delta=max(delta,s[r-1]-s[l-1]-a[r]*(r-l));"

把这两个式子变形,可以得到:

a[l]*(r-l)-(s[r]-s[l])=a[l]*r-a[l]*l-s[r]+s[l]=(a[l]*r-s[r])+(s[l]-a[l]*l)

s[r-1]-s[l-1]-a[r]*(r-l)=a[r]*l-a[r]*r+s[r-1]-s[l-1]=(a[r]*l-s[l-1])+(s[r-1]-a[r]*r)

对于每一个l/r,右面括号里的项都是确定的,现在需要的就是确定左面括号中的最大值

而左面括号的式子形如一个k*x+b的一次函数,所以不难想到维护一个下凸壳,对于每个a[i]在下凸壳中查找

不过,这个式子并没有决策单调性,所以我们不能用单调队列维护,而是一直保存着那个下凸壳,每次用log(n)二分查找

这样就可以解决这个问题了,最后答案依然是ans+delta

代码见下:

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
typedef long long LL;
const int N=200100;
int n;
inline LL max(LL a,LL b){return a>b?a:b;}
LL a[N],s[N],ans1,delta=0;
struct node{LL a,b;};
inline LL f(LL a,node b){return b.a*a+b.b;}
node q[N];int h,t;
inline LL query(LL x)
{
    int le=0,ri=t;
    while(ri-le>1)
    {
        int mi=(le+ri)>>1;
        if(f(x,q[mi])<=f(x,q[mi+1]))
            le=mi;
        else ri=mi;
    }
    return f(x,q[ri]);
}
int main()
{
    scanf("%d",&n);
    for(LL i=1;i<=n;i++)
    {
        cin>>a[i];
        s[i]=a[i]+s[i-1];
        ans1+=a[i]*i;
    }
    t=0;
    for(LL r=2;r<=n;r++)
    {
        node tmp=(node){r-1,-s[r-2]};
        while(t>1&&(q[t].b-tmp.b)*(q[t].a-q[t-1].a)<=(q[t-1].b-q[t].b)*(tmp.a-q[t].a))t--;
        q[++t]=tmp;
        delta=max(delta,query(a[r])-a[r]*r+s[r-1]);
    }
    t=0;
    for(LL l=n-1;l>=1;l--)
    {
        node tmp=(node){-(l+1),-s[l+1]};
        while(t>1&&(q[t].b-tmp.b)*(q[t].a-q[t-1].a)<=(q[t-1].b-q[t].b)*(tmp.a-q[t].a))t--;
        q[++t]=tmp;
        delta=max(delta,query(-a[l])-a[l]*l+s[l]);
    }
    cout<<delta+ans1;
}