Given n non-negative integers a1, a2, ..., an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.
Note: You may not slant the container and n is at least 2.

The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
Example:
Input: [1,8,6,2,5,4,8,3,7] Output: 49
真后悔自己以前没有好好学数学,刚看到这道题,内心是懵逼的, 大概能猜到首尾利用两个游标,来计算最大值。但是没有想到的是:第一,最终两个游标需要相遇;第二,并不需要遍历所有的情况。
其实这个题,最暴力最直观的想法就是遍历所有的情况,寻找最大值。
参考的解法,聪明之处,就是并不需要遍历所有情况,而是遍历,我们需要的值一定会存在的那片区域就好了。
用两个for循环实现的O(n^2)算法超时。苦想不出优化解,参考LeetCode讨论区给出的O(n)算法,以下是该算法的证明和实现。 为了提高效率。我们需要在遍历的过程中剪去无用的情况同时100%保证最大的值能在我们余下的情况中获取到。 在这个问题中,我们初始化一左一右两个游标分别为数组的端点。每一次向数组的中间移动值较小的游标一步,直到两个游标相遇。这个过程中,最大容量100%会被扫描过并获取,以下是证明: 1、给定a1,a2,a3.....an作为输入,假设a10 和 a20是最大容量的情况。我们需要证明左游标会到达a10,并且在这期间,右游标可以到达a20,因此核心问题变成:当左游标在a10且右游标在a21时,下一步的移动是右游标指向a20。 2、因为我们总是移动带有较小值的游标,如果a10>a21,我们会移动把右游标从a21移动到a20。假设a21>a10,则height[a10] x (20-10) < height[a10] x (21-10),与1中假设a10和a20是最大容量不符,因此一定有a10>a21。 3、综上所述:左游标会到达a10,并且在这期间,右游标可以到达a20,由此证明,该算法100%能获取到最大值。
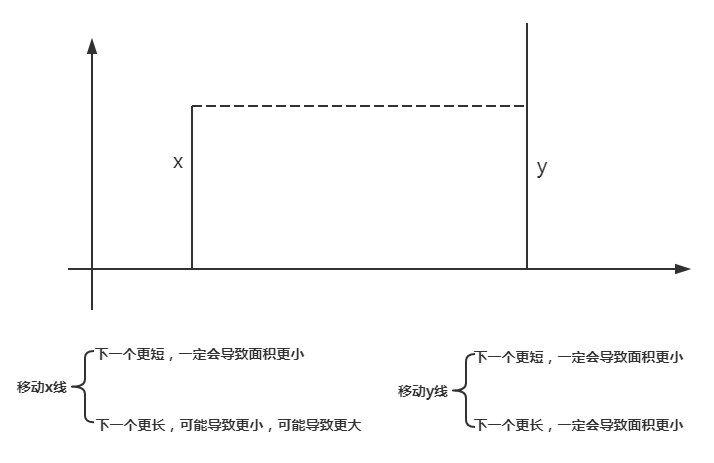
这个解法,就是一定不会错过最大值。所以只有一定x线,才会遇到更大值。那么由此可推,只有每次移动更短的那根线,才能可能遇到最大值。
class Solution { public: int maxArea(vector<int>& height) { int size = height.size(); int max_area = 0; if (size < 2) return 0; int left = 0, right = size - 1; while(left < right) { max_area = max(max_area,(right-left)*min(height[left],height[right])); if (height[left]<height[right]) left++; else right--; } return max_area; } };