题目描述
牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的A到K加上大小王的共5张牌来进行的扑克牌游戏。在斗地主中,牌的大小关 系根据牌的数码表示如下:3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王,而花色并不对牌的大小产生影响。每一局游戏中,一副手牌由 n 张牌组成。游戏者每次可以根据规定的牌型进行出牌,首先打光自己的手牌一方取得游戏的胜利。
现在,牛牛只想知道,对于自己的若干组手牌,分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。
需要注意的是,本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。具体规则如下:
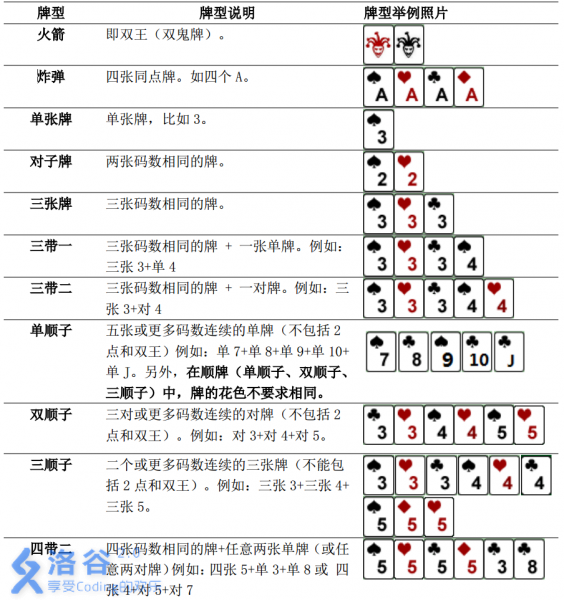
输入输出格式
输入格式
第一行包含用空格隔开的2个正整数 T,n ,表示手牌的组数以及每组手牌的张数。
接下来 T 组数据,每组数据 n 行,每行一个非负整数对 $ a_i , b_i $ ,表示一张牌,其中 $ a_i (表示牌的数码,) b_i $ 表示牌的花色,中间用空格隔开。特别的,我们用 1 来表示数码 A, 11 表示数码J , 121212 表示数码Q,13表示数码 K;黑桃、红心、梅花、方片分别用 1−4 来表示;小王的表示方法为 01 ,大王的表示方法为 02 。
输出格式
共 T 行,每行一个整数,表示打光第 iii 组手牌的最少次数。
输入输出样例
输入样例#1
1 8
7 4
8 4
9 1
10 4
11 1
5 1
1 4
1 1
输出样例#1
3
输入样例#2
1 17
12 3
4 3
2 3
5 4
10 2
3 3
12 2
0 1
1 3
10 1
6 2
12 1
11 3
5 2
12 4
2 2
7 2
输出样例#2
6
样例解释
样例1说明
共有1组手牌,包含8张牌:方片7,方片8,黑桃9,方片10,黑桃J,黑桃5,方片A以及黑桃A。可以通过打单顺子(方片7,方片8,黑桃9,方片10,黑桃J),单张牌(黑桃5)以及对子牌(黑桃A以及方片A)在3次内打光。
对于不同的测试点, 我们约定手牌组数T与张数n的规模如下:
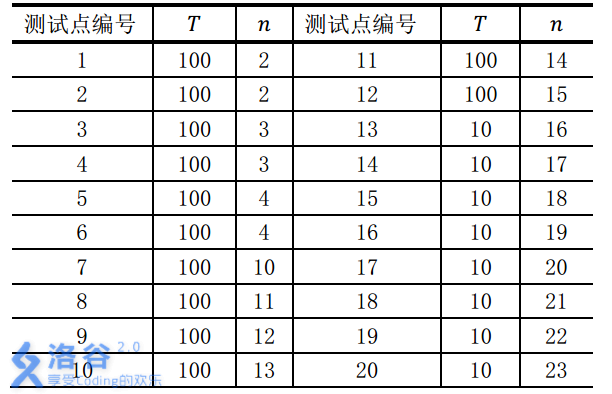
解析
该做法有一个前提,数据是随机的,出牌顺序对后来的决策没有影响。
似乎是一道搜索+贪心+模拟的题目。在所有出牌规则中,我们先寻找形式固定的四带二、三带一、炸弹、三张牌、对子(火箭也算对子)和单张牌。设b[i]表示张数为i的牌有多少种。对于四带二,如果有四张的,我们就依次看b[2]是否大于等于2、b[1]是否大于等于1、b[2]是否大于等于1,。满足条件就按对应情况出牌。三带一同理。每出一次就把带的牌在b中对应的种数减掉。那么最后剩下的b中的值的和就是我们如果要出完手中的牌不计顺子所需要次数。用它去更新答案。注意,这个是有用的,在只能单个组合打出时它能统计答案。然后是顺子。其实每个顺子都差不多,用两重循环在计数数组a中找到满足条件的连续的牌并减去对应的值,如果不连续了就退出。如果连续区间的长度大于要求长度就搜索下一层。记得退出时复原a数组。注意K和A也算是连续的。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#define N 15
using namespace std;
int t,n,i,a[N],ans,len[4]={0,5,3,2};
void dfs(int);
void shunzi(int t,int x)
{
for(int i=1;i<=12;i++){
int k=12;
for(int j=i;j<=12;j++){
a[j]-=t;
if(a[j]<0){
k=j;
break;
}
if(j-i+1>=len[t]) dfs(x+1);
}
for(int j=k;j>=i;j--) a[j]+=t;
}
}
void dfs(int x)
{
int b[5]={0};
for(int i=0;i<=13;i++) b[a[i]]++;
for(int i=1;i<=13;i++){
if(a[i]==4){
if(b[2]>=2) b[2]-=2;
else if(b[1]>=2) b[1]-=2;
else if(b[2]>=1) b[2]--;
}
}
for(int i=1;i<=13;i++){
if(a[i]==3){
if(b[1]>=1) b[1]--;
else if(b[2]>=1) b[2]--;
}
}
ans=min(ans,x+b[1]+b[2]+b[3]+b[4]);
for(int i=1;i<=3;i++) shunzi(i,x);
}
int main()
{
cin>>t>>n;
while(t--){
memset(a,0,sizeof(a));
ans=1<<30;
for(i=1;i<=n;i++){
int x,col;
cin>>x>>col;
if(x==0) a[x]++;
else if(x<=2) a[x+11]++;
else a[x-2]++;
}
dfs(0);
cout<<ans<<endl;
}
return 0;
}