图论学习笔记——LCA

LCA

解法一：Tarjan 【O(n+q)】

流程

初始化fa[i]=i，vis[i]=0.

从树根开始DFS，标记当前搜索中的节点(v)vis[v] = -1。然后搜索其满足(vis[i]=0)的所有子节点(i)。当一个节点(v)的所有子节点均被搜索过（或无子节点）时，则用并查集的合并操作，令(fa[v])为其祖先节点。然后开始查找与节点(v)有询问关系的节点(q)，若(q)已被搜索过（vis[q] = 1），则(LCA(v,q)=find(q))。遍历完有询问关系的节点后，标记(v)已被搜索完毕vis[v] = 1。

离线操作，将(q)个询问以链式前向星双向边的形式存储，也就是说共(2q)条边。当(i)为奇数时，(i)与(i+1)是同样两个节点，答案应该一致，所以在记录答案时代码如下：

for (int i = headq[u]; i; i = eq[i].next) {
        int v = eq[i].to;
        if (vis[v] == 1) {
            lca[i] = find(v);
            if (i % 2) lca[i + 1] = lca[i];
            else lca[i - 1] = lca[i];
        }
    }

完整代码

const int INF = 0x3f3f3f;
const int maxn = 2e6 + 100;

struct Edge {
    int from, to, next; LL w;
}e[maxn * 4], eq[maxn * 4];

int cnt_e = 0, head[maxn], headq[maxn], n, m;
int vis[maxn], fa[maxn];
int lca[maxn];

void add(int head[], Edge e[], int u, int v) {
    e[++cnt_e].next = head[u]; e[cnt_e].from = u; e[cnt_e].to = v; head[u] = cnt_e;
}

int find(int x) {
    return x == fa[x] ? x : fa[x] = find(fa[x]);
}

void merge(int x, int y) {
    int a = find(x);
    int b = find(y);
    if (a != b) {
        fa[a] = b;
    }
}

void tarjan(int u) {
    vis[u] = -1;
    //标记u正在搜索，防止来回dfs死循环
    for (int i = head[u]; i; i = e[i].next) {
        int v = e[i].to;
        if (!vis[v]) {
            //只有未搜索过的子节点才能继续搜索
            tarjan(v);
            merge(v, u);
        }
    }
    //查找与u有询问关系的节点
    for (int i = headq[u]; i; i = eq[i].next) {
        int v = eq[i].to;
        if (vis[v] == 1) {
            //v已经搜索过，则u和v的最近公共祖先就是v的祖先
            lca[i] = find(v);
            //存询问的时候存了双向边，两条边答案应该一致
            if (i % 2) lca[i + 1] = lca[i];
            else lca[i - 1] = lca[i];
        }
    }
    vis[u] = 1;
    //标记节点u（及其所有子节点）已经搜索完毕
}

int main() {
    int q, s;
    cin >> n >> q >> s;
    for (int i = 1; i <= n; i++) fa[i] = i;
    for (int i = 1; i <= n - 1; i++) {
        int u, v;
        cin >> u >> v;
        add(head, e, u, v);
        add(head, e, v, u);
    }
    cnt_e = 0;
    //建新图之前记得初始化这个
    for (int i = 1; i <= q; i++) {
        int u, v;
        cin >> u >> v;
        add(headq, eq, u, v);
        add(headq, eq, v, u);
    }
    tarjan(s);
    for (int i = 1; i <= q; i++) {
        cout << lca[i*2] << endl;
    }
    return 0;
}

解法二：倍增 【O((n+q)logn)】

导入

容易想到这样一种求LCA的暴力解法：对于节点(u),(v)，一直向上查找它们的父节点/祖先节点(root_u)和(root_v)，直到(root_u=root_v)，此时就得到了它们的LCA。

显然这样的做法非常耗时，能不能把步子迈大一点呢？

我们有这么一个结论：任意正整数(k)，都可以表示为(2^i)之和（如(9=2^3+2^0)）。

也就是说，无论我们要向上跳多少层，都可以用这样的方法在(log_2n)步后跳到。

如果将逐步向上查找改为(2^i)次方地往上跳（比如一口气先向上跳8层，再接着向上跳4层，2层……逐渐接近最近公共祖先），时间将优化为(O((n+q)logn))

流程

令(lg[i])的值为(log_2i+1)（其中(log_2i)向下取整），预处理算出。（其实是一种常数优化）

    lg[0] = 0;
	for (int i = 1; i <= n; i++) {
        lg[i] = lg[i - 1] + (1 << lg[i - 1] == i);
    }

用(depth[i])记录节点(i)的深度，(fa[i][j])记录节点(i)的第(2^j)级祖先，同样预处理算出。

（注：节点(i)的第(1)级祖先即它的父节点，第(2)级祖先即它的爷爷节点，以此类推）

void dfs(int u, int pre) {
    //u为当前节点，pre为u的父节点
    fa[u][0] = pre;
    depth[u] = depth[pre] + 1;
    for (int i = 1; i <= lg[depth[u]]; i++) {
        //这里体现了lg数组的用处：用u的深度来推出要倍增跳几次才能跳到树根
        fa[u][i] = fa[fa[u][i - 1]][i - 1];
        //这一行是倍增的核心
        //意思是节点u的2^i级祖先就是它2^(i-1)级祖先的2^(i-1)级祖先
        //比如，节点u的爷爷节点(2级祖先)就是它父节点(1级祖先)的父节点(1级祖先)
    }
    for (int i = head[u]; i; i = e[i].next) {
        if (e[i].to != pre) dfs(e[i].to, u);
        //加一个判断，确保向着子节点dfs
    }
}

设询问LCA的两个节点分别为(u)和(v)，先将其中更深的节点拉到和另一个节点同一深度。如果刚好拉到了另一个节点上，这个深度浅的节点就是LCA。否则，尝试从最大的步子开始迈，如果会一下迈到公共祖先，说明步子太大，幂次需要减小；如果不会迈到公共祖先，就让两个节点都跳上去，继续逼近LCA。

int LCA(int u, int v) {
    if (depth[u] < depth[v]) swap(u, v);
    //不妨设u的深度＞v的深度
    while (depth[u] > depth[v]) {
        u = fa[u][lg[depth[u] - depth[v]] - 1];
        //将更深的节点u拉到和v同一深度
    }
    if (u == v) return v;
    for (int k = lg[depth[u]] - 1; k >= 0; k--) {
        //倍增的核心之二
        if (fa[u][k] != fa[v][k]) {
            //先尝试迈最大的步子，一步跳2^(lg[depth[u]]-1)这么多层
            //如果相同，说明会跳到公共祖先，也就是步子太大，幂次要小一点
            //如果不相同，说明可以继续往上跳，更加逼近LCA
            //目标是跳到LCA所在深度的下面一层
            u = fa[u][k];
            v = fa[v][k];
        }
    }
    return fa[u][0];
    //u和v跳到了LCA的下面一层，父节点就是LCA
}

完整代码

const int INF = 0x3f3f3f;
const int maxn = 2e6 + 100;

struct Edge {
    int from, to, next; LL w;
}e[maxn * 4], eq[maxn * 4];

int cnt_e = 0, head[maxn], n, m;
int fa[maxn][22];//2的22次方是四百多万，小于n
int depth[maxn], lg[maxn];

void add(int head[], Edge e[], int u, int v) {
    e[++cnt_e].next = head[u]; e[cnt_e].from = u; e[cnt_e].to = v; head[u] = cnt_e;
}
void addw(int head[], Edge e[], int u, int v, LL w) {
    e[++cnt_e].next = head[u]; e[cnt_e].from = u; e[cnt_e].to = v; e[cnt_e].w = w; head[u] = cnt_e;
}

void dfs(int u, int pre) {
    //u为当前节点，pre为u的父节点
    fa[u][0] = pre;
    depth[u] = depth[pre] + 1;
    for (int i = 1; i <= lg[depth[u]]; i++) {
        //lg数组的用处：用u的深度来推出要两级两级地跳几次才能跳到树根
        fa[u][i] = fa[fa[u][i - 1]][i - 1];
        //这一行是倍增的核心
        //意思是节点u的2^i级祖先就是它2^(i-1)级祖先的2^(i-1)级祖先
        //比如，节点u的爷爷节点(2级祖先)就是它父节点(1级祖先)的父节点(1级祖先)
    }
    for (int i = head[u]; i; i = e[i].next) {
        if (e[i].to != pre) dfs(e[i].to, u);
        //加一个判断，确保向着子节点dfs
    }
}

int LCA(int u, int v) {
    if (depth[u] < depth[v]) swap(u, v);
    //不妨设u的深度＞v的深度
    while (depth[u] > depth[v]) {
        u = fa[u][lg[depth[u] - depth[v]] - 1];
        //将更深的节点u拉到和v同一深度
    }
    if (u == v) return v;
    for (int k = lg[depth[u]] - 1; k >= 0; k--) {
        if (fa[u][k] != fa[v][k]) {
            //跳到LCA的下面一层即可
            u = fa[u][k];
            v = fa[v][k];
        }
    }
    return fa[u][0];
    //u和v跳到了LCA的下面一层，父节点就是LCA
}

int main() {
    int q, s;
    cin >> n >> q >> s;
    for (int i = 1; i <= n; i++) {
        lg[i] = lg[i - 1] + (1 << lg[i - 1] == i);
    }
    for (int i = 1; i <= n - 1; i++) {
        int u, v;
        cin >> u >> v;
        add(head, e, u, v);
        add(head, e, v, u);
    }
    //预先算出log_2(i)+1的值，其中log_2(i)向下取整
    dfs(s, 0);
    //预处理出depth[i]和fa[i][j]
    for (int i = 1; i <= q; i++) {
        int u, v;
        cin >> u >> v;
        cout << LCA(u, v) << endl;
    }
    return 0;
}

解法三：RMQ【O(nlogn)+O(1)】

RMQ算法预处理(O(nlogn))， 查询(O(1))，适合询问量很大的情形。

预备知识

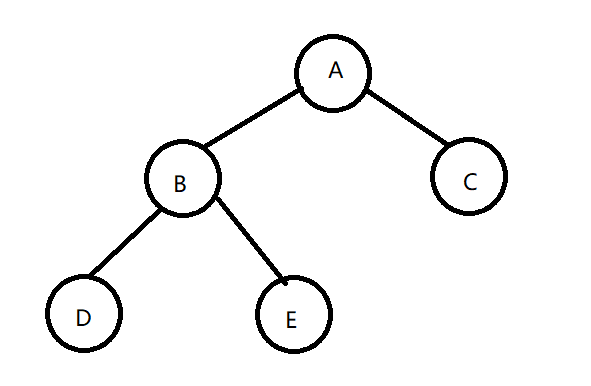
DFS序：对一棵树进行DFS时，对每个结点开始访问时的顺序。

欧拉序：对一棵树进行DFS时，对每个结点开始访问和结束访问（注意这里的结束访问是当结束了它的一棵子树所有访问时）的顺序。

对于上图的树，

DFS序为：A→B→D→E→C；

欧拉序为：A→B→D→B→E→B→A→C→A

括号定理：对一棵树进行DFS，记录每一个节点出入栈的时间，则可以将树转化为线性结构。记节点(u)的入栈时间为(in[u])，出栈时间为(out[u])，则在时间区间([in[u],out[u]])内出入栈的节点必属于(u)的子树。

ST表：https://www.cnblogs.com/streamazure/p/13889947.html

导入

容易想到，两个节点的最近公共祖先就是囊括了这两个节点的最小子树的根。

如何得到这个根？再观察一下欧拉序，只要在(u)开始访问到(v)开始访问这段区间内找到深度最浅的节点即可。

维护区间的数据结构有很多，比如线段树。但对于这个问题，我们用更快的ST表解决。

ST表的应用关键在于重叠区间不会影响问题的结果，所以它可以求得区间最值问题，但不能求区间和。对于LCA问题，我们要找的是区间内深度值最浅的点，这也是个区间最值问题，故可以应用ST表。

注意事项

• 因为一个点会多次进出，存储欧拉序的数组要开得很大才够用
• ST表预处理的时候记得把边界改为tot（欧拉序数组的长度），别直接套模板照搬n，这里的n是节点数。
• 查询的时候用节点首次出现的时间作为左右端点

完整代码

const int maxn = 4e6 + 100;

struct Edge {
    int from, to, next; LL w;
}e[maxn * 4];

int cnt_e = 0, head[maxn], n, m;
int fa[maxn][22];//2的22次方是四百多万，小于n
int depth[maxn],st[maxn][22], lg[maxn];
int dfn[maxn], fir[maxn];
//因为一个点会多次进出，欧拉序数组需要开得很大
//fir记录一个点首次出现的时间
int tot = 0;

void add(int head[], Edge e[], int u, int v) {
    e[++cnt_e].next = head[u]; e[cnt_e].from = u; e[cnt_e].to = v; head[u] = cnt_e;
}

void ST() {
    //ST表预处理部分
    lg[0] = -1;
    for (int i = 1; i <= tot; i++) {
        lg[i] = lg[i / 2] + 1;
    }
    for (int j = 1; j <= lg[tot]; j++) {
        //枚举区间长度
        //注意边界！！st数组的长度是tot不是n！！
        for (int i = 1; i + (1 << j) - 1 <= tot; i++) {
            //注意边界！！st数组的长度是tot不是n！！
            //注意f数组中储存的是一段时间区间内最小深度值所对应的节点，没有直接储存深度值
            int x = st[i][j - 1];
            int y = st[i + (1 << (j - 1))][j - 1];
            if (depth[x] < depth[y]) st[i][j] = x;
            else st[i][j] = y;
        }
    }
}

void dfs(int u,int pre) {
    //预处理出欧拉序和深度
    dfn[++tot] = u;
    if (!fir[u]) fir[u] = tot;
    depth[u] = depth[pre] + 1;
    st[tot][0] = u;
    //ST表预处理部分，记录一个时刻对应的节点
    //记录开始访问的时间
    for (int i = head[u]; i; i = e[i].next) {
        int v = e[i].to;
        if (v != pre) {
            dfs(v, u);
            dfn[++tot] = u;
            st[tot][0] = u;
            //ST表预处理部分，记录结束访问时刻对应的节点
            //这一行记得写在大括号里！！只有在真的访问到子节点的时候才执行
        }
    }
}

int LCA(int l, int r) {
    //ST表查询部分
    int k = lg[r - l + 1];
    int x = st[l][k];
    int y = st[r - (1 << k) + 1][k];
    if (depth[x] < depth[y]) return x;
    else return y;
}

int main() {
    int s;
    cin >> n >> m >> s;
    for (int i = 1; i <= n - 1; i++) {
        int u, v;
        cin >> u >> v;
        add(head, e, u, v);
        add(head, e, v, u);
    }
    dfs(s, 0);
    ST();
    for (int i = 1; i <= m; i++) {
        int l, r;
        cin >> l >> r;
        if (fir[l] > fir[r]) swap(l, r);
        cout << LCA(fir[l], fir[r]) << endl;
        //序列的下标就是时间，要找出节点对应的开始访问时间作为区间端点
    }
    return 0;
}

解法四：树链剖分