考虑一个节点一个节点加入树中,每次计算一下对答案的贡献
只有两个点时树的形态是唯一确定的
三个点时第三个点应该是从边上分叉出来的
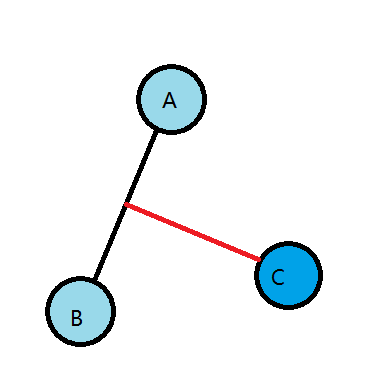
那么增加的长度显然为 (dis_bc+dis_ac-dis_ab)/2
第四个点也应该是分叉出来的
但是是从哪分叉的我们还要讨论一下
可以发现,唯一合法的情况当且仅当增加的长度最小
因为如果增加的长度大于最小的增长长度,那么必定会有某些约束条件被破坏
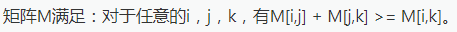
这个自己画图一下就可以发现的
所以每次加点时必须找增加长度最小的方案
然后就可以暴力枚举了
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cmath> using namespace std; inline int read() { int x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*f; } const int N=57,INF=1e9+7; int n,ans; int mp[N][N]; int main() { n=read(); while(n) { for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) mp[i][j]=mp[j][i]=read(); ans=0; for(int k=2;k<=n;k++) { int mi=INF; for(int i=1;i<k;i++) for(int j=1;j<k;j++) mi=min(mi,(mp[i][k]+mp[j][k]-mp[i][j])>>1);//枚举最小的方案 ans+=mi;//加入答案 } printf("%d ",ans); n=read(); } return 0; }