| 项目 | 内容 |
|---|---|
| 课程班级博客链接 | 班级博客 |
| 这个作业要求链接 | 作业要求 |
| 我的课程学习目标 | (1)了解常用源代码管理工具与开发工具; (2)掌握软件项目个人开发流程; (3)掌握Github发布软件项目的操作方法。 |
| 这个作业在哪些方面帮助我实现学习目标 | (1)通过评论相关作业博客,对常用源代码管理与开发工具的了解更加系统化; (2)通过阅读《构建之法》第1,2章,对PSP流程有清晰的了解; (3)通过背包问题的程序开发,掌握了软件项目个人开发流程以及Github发布软件项目的操作方法。 |
| 项目Github的仓库链接地址 |
一.实验内容与步骤
任务1:阅读教师博客“常用源代码管理工具与开发工具”内容要求,点评班级博客中已提交相关至少3份作业。
作业点评链接如下:
点评一:201871030136
点评二:201871030131
点评三:201871030125
点评四:201871030116
任务2:详细阅读《构建之法》第1章、第2章,掌握PSP流程。
- 通过阅读《构建之法》后,学习了第1章主要讲的开发的不同阶段:玩具阶段、业余爱好阶段、探索阶段、成熟的产业阶段;软件工程的定义是:把系统的、有序的、可量化的方法应用到软件的开发、运营和维护上的过程;软件的特殊性:复杂性、不可见性、易变性、服从性、非连续性。计算基础、数学基础、工程基础是软件工程的三大类基础知识领域;我了解到软件工程真正的样子是软件=程序+软件工程。软件工程不仅仅是简单的软件开发的过程。
- 第二章主要讲了单元测试、回归测试、效能分析、个人软件开发流程。这一章讲述了一个好的软件工程师应该怎样合理分析软件错误并明确各个模块功能和提高效能还有如何管理自己的源代码。并且这一章还给了我们锻炼编程基本功的方法和如何实践的过程。学习结束之后对 PSP 有了相关重点的总结如下:
1. 什么是PSP
- 它是一个自我改进的过程,它帮助控制、管理和改进自己的工作方式
- 它是一个结构化的框架,包括了软件开发中使用的表格、准则和规程
- 它提供了一个度量和分析框架,用来检验和管理你的个人工作
- 它还是一个已定义过程,用来帮助你改善自己的个人绩效
2.通过理论学习和具体项目的练习要做到三点
- 研发出符合用户需求的软件说明;
- 通过一定的软件流程,在预计的时间内发布“足够好”的软件说明;
- 并通过数据和其他方式展现所开发的软件是可以维护和继续发展的说明。
3.个人软件开发流程PSP:PSP包括计划、开发和报告三个阶段,每个阶段又包含了多个任务。
- 计划:估计这个任务需要多少时间,并规划大致步骤;
- 开发:需求分析、生成设计文档、设计复审、代码规范、具体设计、具体编码、代码复审、测试;
- 报告:测试报告、计算工作量、事后总结并提出过程改进计划。
4.PSP的特点
- 不局限于某一种软件技术(如编程语言),而是着眼于软件开发的流程,这样,开发不同应用的软件工程师可以互相比较。
- 不依赖于考试,而主要靠工程师自己收集数据,然后分析,提高。
- 在小型、初创的团队中,很难找到高质量的项目需求,这意味着给程序员的输入质量不高。在这种情况下,程序员的输出往往质量也不高,然而这并不能全部由程序员负责。
- PSP依赖于数据。
- 需要工程师输入数据,记录工程师的各项活动,这本身就需要不小的时间代价。
- PSP的目的是记录工程师如何实现需求的效率,而不是记录顾客对产品的满意度。
阅读完《构建之法》第1、2章后,对PSP流程有了清晰的认识,PSP的流程及各个阶段如下表所示:
| PSP | 任务内容 |
|---|---|
| Planning - Estimate |
计划 - 估计这个任务需要多少时间 |
| Development - Analysis - Design Spec - Design Review - Coding Standard - Design - Coding - Code Review - Test |
开发 - 分析需求 - 生成设计文档 - 设计复审(和同事审核设计文档) - 代码规范(为目前的开发制定合适的规范) - 具体设计 - 具体编码 - 代码复审 - 测试(包括自测,修改代码,提交修改) |
| Record TimeSpent | 记录用时 |
| Test Report | 测试报告 |
| Size Measurement | 计算工作量 |
| Postmortem | 事后总结 |
| Process Improvement Plan | 提出过程改进计划 |
任务3:项目开发
开发背景:背包问题(Knapsack Problem,KP)是NP Complete问题,也是一个经典的组合优化问题,有着广泛而重要的应用背景。
{0-1}背包问题({0-1 }Knapsack Problem,{0-1}KP)是最基本的KP问题形式,它的一般描述为:从若干具有价值系数与重量系数的物品(或项)中,选择若干个装入一个具有载重限制的背包,如何选择才能使装入物品的重量系数之和在不超过背包载重前提下价值系数之和达到最大?D{0-1} KP 是经典{ 0-1}背包问题的一个拓展形式,用以对实际商业活动中折扣销售、捆绑销售等现象进行最优化求解,达到获利最大化。D{0-1}KP数据集由一组项集组成,每个项集有3项物品可供背包装入选择,其中第三项价值是前两项之和,第三项的重量小于其他两项之和,算法求解过程中,如果选择了某个项集,则需要确定选择项集的哪个物品,每个项集的三个项中至多有一个可以被选择装入背包,D{0-1} KP问题要求计算在不超过背包载重量 的条件下,从给定的一组项集中选择满足要求装入背包的项,使得装入背包所有项的价值系数之和达到最大;D{0-1}KP instances数据集是研究D{0-1}背包问题时,用于评测和观察设计算法性能的标准数据集;动态规划算法、回溯算法是求解D{0-1}背包问题的经典算法。
1. 需求分析。
背包问题(Knapsack problem)是一种组合优化的NP完全问题。通过不同的方法(如回溯法,动态规划法)来解决背包问题。问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。现在,我使用动态规划算法来解决0-1背包问题,在这次的个人项目中,可以在项目中实现从文件中读入需要的数据,可以用散点图表示价值与重量之间的关系,将控制台上的所有内容导出到文本文档中。
(1)D{0-1}KP即折扣0-1背包问题,通过刻画大型商业物资采购、折扣促销等现象,利用数学模型对问题进行优化求解,以达到目标函数最优的目标。其目标为利润最大化。D{0-1}KP的应用场景宽广。
(2)条件:不超过背包载重量,从项集中选择满足要求装入背包的项,使得装入背包所有项的价值系数之和达到最大。
(3)程序应包含动态规划和回溯两个算法。
2. 功能设计。
- 基本功能
- 可正确读入实验数据文件的有效D{0-1}KP数据;
- 能够绘制任意一组D{0-1}KP数据以重量为横轴、价值为纵轴的数据散点图;
- 能够对一组D{0-1}KP数据按项集第三项的价值:重量比进行非递增排序;
- 用户能够自主选择动态规划算法、回溯算法求解指定D{0-1} KP数据的最优解和求解时间(以秒为单位);
- 任意一组D{0-1} KP数据的最优解、求解时间和解向量可保存为txt文件或导出EXCEL文件。
3. 设计实现。
(1)ReadTheFil类 :通过文件路径来创建文件实例,把FileInputStream实例 传递到 BufferedInputStream,目的是能快速读取文件,最后,使用available检查是不是读到了文件末尾。
(2)ScatterDiagram类 :创建二维数组data存储profit价值和height重量,以重量为横轴、价值为纵轴,建立直角坐标系画出散点图。
(3)WeightRatio类 :分别定义int类型数组profit和weight数组将价值和重量存储,因为所给数据全部为int型,再定义比值ratio为double类型,再将其int类型数组强制转换为double进行比值运算,最后运用冒泡排序将比值进行降序排序。
(4)Time类 :使用动态规划算法在背包问题中,物品或者被装入背包,或者不被装入背包,设xi表示物品i装入背包的情况,则当xi=0时,表示物品i没有被装入背包,xi=1时,表示物品i被装入背包。
(5)正确读入实验数据文件的有效D{0-1}KP数据:currentTimeMillis():该方法的作用是返回当前的计算机时间,时间的表达格式为当前计算机时间和GMT时间(格林威治时间)1970年1月1号0时0分0秒所差的毫秒数。字符流LineNumberReader():LineNumberReader是BufferedReader的子类, 具有相同的功能, 并且可以统计行号。
(6)绘制任意一组D{0-1}KP数据以重量为横轴、价值为纵轴的数据散点图:JPanel 是 Java图形用户界面(GUI)工具包swing中的面板容器类,包含在javax.swing 包中,是一种轻量级容器,可以加入到JFrame窗体中。JPanel默认的布局管理器是FlowLayout,其自身可以嵌套组合,在不同子容器中可包含其他组件(component),如JButton、JTextArea、JTextField 等,功能是对窗体上的这些控件进行组合,相当于C++和C#中的Panel类。
(7)对一组D{0-1}KP数据按项集第三项的价值:重量比进行非递增排序:Quicksort;快速排序由C. A. R. Hoare在1960年提出。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
(8)用户自主选择动态规划算法、回溯算法求解指定D{0-1} KP数据的最优解和求解时间(以秒为单位):currentTimeMillis();该方法的作用是返回当前的计算机时间,时间的表达格式为当前计算机时间和GMT时间(格林威治时间)1970年1月1号0时0分0秒所差的毫秒数。
动态规划算法:动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,我们希望找到具有最优值的解。动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。
4. 测试运行。
绘制散点图:对idkp1-10.txt文件中的第一组数据IDKP0绘制散点图。初始化背包容量capacity=10149,物品的个数number=30,将第一组数据存放在列表weight和profit中。

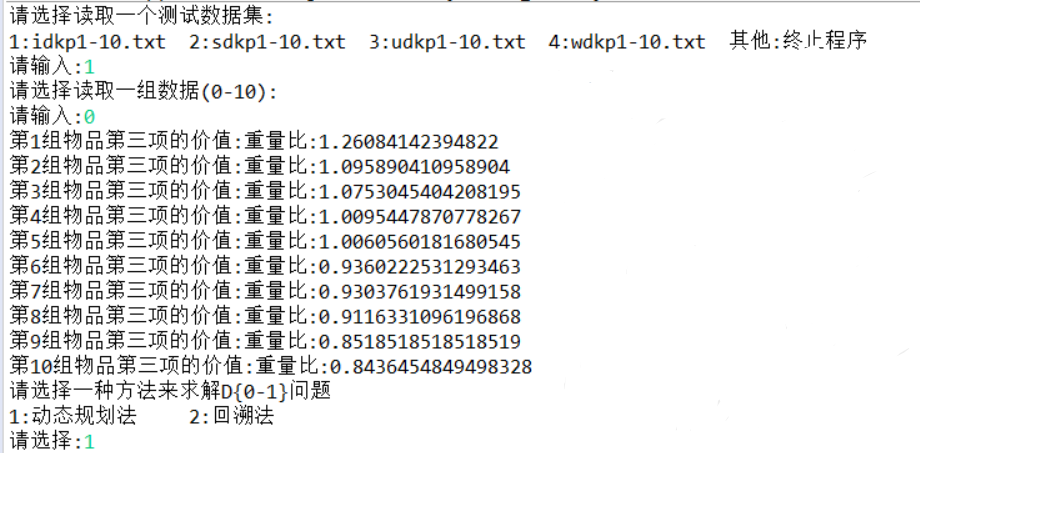
动态规划:
6. 代码片段。
for(int i=1;i<=分组个数;i++){
for(int j=背包总重;j>=0;j--) {
for(int k=1;k<=每组物品个数;k++) {
if(weight[i][k]>j) {
continue;
}
if(dp[j]<dp[j-weight[i][k]]+value[i][k]) {
dp[j]=dp[j-weight[i][k]]+value[i][k];
}
}
}}
6. 总结:你设计的程序如何实现软件设计的“模块化”原则。
软件设计的 “模块化”原则就是把软件整体划分,将每一个划分后的块逐个完成后再组成软件。这些块之间相对独立,之间用接口(协议) 通信,每个块完成一个功能,通过多个块组合可以完成一列功能。所以在此次软件任务设计中,通过将背包问题所需要完成的各个功能进行分解,用一个模块去完成一个一个功能,最后将各个模块进行整合,完成整体的软件设计。
7. 展示PSP如下图。
| PSP2.1 | 任务内容 | 划共完成需要的时间(min) | 实际完成需要的时间(min) |
|---|---|---|---|
| Planning | 计划 | 15 | 10 |
| · · Estimate | · 估计这个任务需要多少时间,并规划大致工作步骤 | 10 | 10 |
| development | 开发 | 800 | 880 |
| · · Analysis | · 需求分析 (包括学习新技术) | 30 | 20 |
| · · Design Spec | · 生成设计文档 | 25 | 20 |
| · · Design Review | · 设计复审 (和同事审核设计文档) | 20 | 20 |
| · · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 30 | 27 |
| · · Design | 具体设计 | 20 | 12 |
| · · Coding | · 具体编码 | 120 | 80 |
| · · Code Review | · 代码复审 | 19 | 30 |
| · · Test | · 测试(自我测试,修改代码,提交修改) | 30 | 40 |
| Reporting | 报告 | 20 | 40 |
| · · Test Report | · 测试报告 | 20 | 28 |
| · · Size Measurement | · 计算工作量 | 5 | 5 |
| · · Postmortem & Process Improvement Plan | · 事后总结 ,并提出过程改进计划 | 5 | 8 |
任务4:完成任务3的程序开发,将项目源码的完整工程文件提交到你注册Github账号的项目仓库中。
二.实验总结
通过本次实验,首先浏览了其他同学的博客作业,借助同学的总结对常用源代码管理与开发工具的了解更加系统化,了解了他们之间的基础特点与异同点;然后通过阅读《构建之法》第1,2章,对PSP流程有清晰的了解;对本次实验中的项目开发有了很大的帮助;本次作业的核心是背包问题的程序开发,在完成本次作业的过程中时占比最长,PSP的各个阶段中,由于编程能力的薄弱,在代码开发过程中遇到了较大的难题,导致没有在预想的时间段内完成该阶段的任务;通过这个开发项目,让我对背包问题这一经典的组合优化问题有了基础的了解,同时借助这个项目,掌握了软件项目个人开发流程以及Github发布软件项目的操作方法,对自己之后的学习也有很大的帮助。