湖南集训day7

难度:☆☆☆☆☆☆

/*
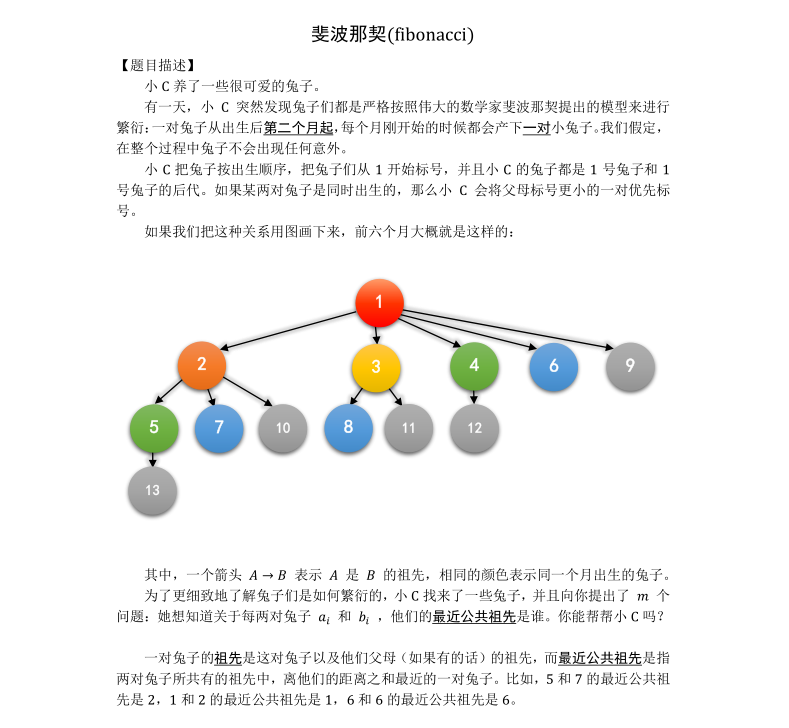
由观察可知 同种颜色的减去他的父亲值相同
我们考虑把询问的两个数分别减去小于它的最大斐波那契数。
*/
#include<iostream>
#include<cstdio>
#include<cstring>

#define N 3000007
#define ll long long

using namespace std;
ll n,m,x,y,ans,cnt1,cnt2;
ll feb[N];

inline ll read()
{
    ll x=0,f=1;char c=getchar();
    while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}

inline ll swap(ll x, ll y)
{
    ll tmp=x;x=y;y=tmp;
}

int main()
{
    freopen("fibonacci.in","r",stdin);
    freopen("fibonacci.out","w",stdout);
    feb[1]=feb[2]=1;
    for(int i=3;i<=60;i++) feb[i]=feb[i-1]+feb[i-2];
    m=read();
    while(m--)
    {
        x=read();y=read();
        for(int i=60;x!=y;i--)
        {
            if(x>feb[i]) x-=feb[i];
            if(y>feb[i]) y-=feb[i];
        }
        printf("%lld
",x);
    }
    fclose(stdin);fclose(stdout);
    return 0;
}

/*
在vector里二分左右端点计算答案即可
也可以用动态开点线段树
分块和主席树写好看了应该也能搞过去
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>

#define N 300010

using namespace std;
vector<int>a[300010];
int pos[N];
int n,m,l,r,k,x;

inline int read()
{
    int x=0,f=1;char c=getchar();
    while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}

int main()
{
    n=read();m=read();
    for(int i=1;i<=n;i++) pos[i]=read(),a[pos[i]].push_back(i);
    for(int i=1;i<=300000;i++) 
      sort(a[i].begin(),a[i].end());
    for(int i=1;i<=m;i++)
    {
        int opt;opt=read();
        if(opt==1)
        {
            l=read();r=read();k=read();
            int ll=0,rr=a[k].size()-1,ans=-1,mid;
            while(ll<=rr)
            {
                mid=ll+rr>>1;
                if(a[k][mid]>=l) ans=mid,rr=mid-1;
                else ll=mid+1;
            }
            if(ans==-1){printf("0
");continue;}
            ll=0,rr=a[k].size()-1;int ans2=-1;
            while(ll<=rr)
            {
                int mid=ll+rr>>1;
                if(a[k][mid]<=r) ans2=mid,ll=mid+1;
                else rr=mid-1;
            }
            if(ans2==-1){printf("0
");continue;}
            else printf("%d
",ans2-ans+1);
        }
        else
        {
            x=read();
            if(pos[x]==pos[x+1]) continue;
            else 
            {
                a[pos[x]][lower_bound(a[pos[x]].begin(),a[pos[x]].end(),x)-a[pos[x]].begin()]++;
                a[pos[x+1]][lower_bound(a[pos[x+1]].begin(),a[pos[x+1]].end(),x+1)-a[pos[x+1]].begin()]--;
                swap(pos[x],pos[x+1]);
            }
        }
    }
}

/*
k==1 从后往前找最长的不冲突的，这样可以保证字典序最小
枚举k,k*k-a[i]==a[j]说明a[i]与a[j]的和是一个完全平方数。

k==2 部分分可以二分图染色
用并查集“敌人集合”维护冲突关系。
注意特判数相等的情况(k*k==a[j]*2) 
*/
#include<iostream>
#include<cstdio>
#include<cstring>

#define N 131073

using namespace std;
int n,m,K;
int a[N],b[N],f[N<<1];
bool vis[N],dvis[N],issqr[N<<1];

inline int read()
{
    int x=0,f=1;char c=getchar();
    while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}

int find(int x){
    return f[x]>0?(f[x]=find(f[x])):x;
}

void merge(int u,int v)
{
    u=find(u),v=find(v);
    if(u!=v)
    {
        if(f[u]>f[v]) swap(u,v);
        f[u]+=f[v];f[v]=u;
    }
}

bool check(int u,int v)
{
    int r1=find(u),r2=find(u+N);
    int s1=find(v),s2=find(v+N);
    if(r1==s1 || r2==s2) return true;
    merge(r1,s2);merge(r2,s1);
    return false;
}

void solve1()
{
    for(int i=n,j=n;i;)
    {
        for(bool flag=1;j;j--)
        {
            for(int k=1;k*k-a[j]<N;k++)
            {
                if(k*k-a[j]<=0) continue;
                if(vis[k*k-a[j]])
                {
                    flag=0;break;
                }
            }
            if(!flag) break;vis[a[j]]=1;
        }
        if(!j) break;b[++m]=j;
        for(;i>j;i--) vis[a[i]]=0;        
    }
}

void solve2()
{
    memset(f,-1,sizeof f);
    for(int i=1;i*i<2*N ;i++) issqr[i*i]=1;
    for(int i=n,j=n;i;)
    {
        for(bool flag=1;j;j--)
        {
            if (vis[a[j]])
            {
                if (issqr[a[j]+a[j]])
                {
                    if (dvis[a[j]]) break;
                    for (int k=1;k*k-a[j]<N;k++)
                    {
                        if (k*k-a[j]<=0) continue;
                        if (vis[k*k-a[j]] &&k*k!=a[j]*2)
                        {
                            flag=0;break;
                        }
                    }
                    if (!flag)break; dvis[a[j]]=1;
                }
            }
            else
            {
                for(int k=1;k*k-a[j]<N;k++)
                {
                    if(k*k-a[j]<=0) continue;
                    if(vis[k*k-a[j]])
                    {
                        if(check(k*k-a[j],a[j]))
                        {
                            flag=0;break;
                        }
                    }
                }
                if(!flag) break;vis[a[j]]=1;
            }
        }
        if(!j) break;b[++m]=j;
        for(;i>j;i--) f[a[i]]=f[a[i]+N]=-1,vis[a[i]]=0,dvis[a[i]]=0;
    }
}

int main()
{
    freopen("division.in", "r", stdin);
    freopen("division.out", "w", stdout);
    scanf("%d%d",&n,&K);
    for (int i=1;i<=n;i++) 
      scanf("%d",&a[i]);
    if (K==1) solve1();
    else solve2();
    printf("%d
",m+1);
    for (int i=m;i;i--) printf("%d ",b[i]);
    putchar('
');
    return 0;
}