多项式前置技能——复数

复数的基本概念

1.复数的形式

记   .我们把形如 a+bi（ a,b 均为实数）的数称为复数.

2.虚数单位

 类似的单位可以推比至 π ,在计算中,我们用 π 来表示圆周率. 其中 π 即为 3.1415926.... 

同样的, a+bi 中的 i 即表示一个虚数单位. 其中  .

3.实部和虚部的概念

在 a+bi 中, 我们称 a 为该复数的实部.

　　　　　　        b 为该复数的虚部.

4.纯虚数,复数,和实数的区分

我们把形如 bi 的数 成为 纯虚数.  如 : 5i , 0.8i ,0.3i .

然后复数即上文所述,然后关于三者的韦恩图是这样子的:

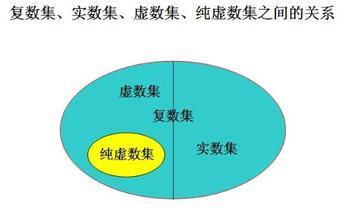
关于复数的基本概念就如上文所书.

 

复数在几何中的引用

1.复平面

在平面内引两条坐标轴,

其中横坐标单位为实数,表示复数的实部大小.

然后纵轴的单位即为 复数单位 i .

2.复数与向量的关系

在复平面的坐标系中,复数 a+bi 可以被表示为 向量 (a,b) 

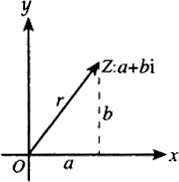
如图坐标轴中的向量即表示 复数 a+bi.

 

3.共轭复数

共轭复数：对于复数 z=a+bi，对于另外一个复数 z′=a-bi，我们称 z′z′ 为 zz 的共轭复数，记做 z⎯⎯ 。

容易发现，一个复数与其共轭复数的实部相等，虚部互为相反数。

 

在引入了复数和向量的关系之后,我们可以更好地理解共轭复数的概念,用向量来解释,共轭复数就是两个大小相同,关于x轴对称的向量.

 

4.复数的幅角

 

我们可以将复数 z 写成 z=r×(cosθ+isinθ)，其中 r 为复数 z 的模长， θ 为复数 z 的辐角。

 

复数的幅角与 θ 普通平面直角坐标系中直线的倾斜角比较相似.

一个复数有多个辐角，这些值相差 2π.

其中,我们将

θ∈[−π,π)θ∈[−π,π) 的 θθ 叫做辐角的主值.

 

 

复数的基本运算

对于复数(a,b)和(c,d).

满足加法法则 (a,b)±(c,d)=(a±c,c±d).

满足乘法法则 (a,b)×(c,d)=(ac−bd,bc+ad) .

对于除法，只需分子分母同乘分母的共轭复数，将分母实数化，分子做复数乘法即可.

  复数乘法的几何意义：模长相乘，幅角相加。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　——引自 NaVi_Awson

 

复数的单位根

关于复数的单位根

 

这方程的复数根 z为n次单位根.

 

关于这些根在复平面中的分布,是这样子的.

 

当 n=1 时 , 它有唯一的根 ( 1 , 0 ) . 因为该向量本身就为 1.

当 n=2 时 , 它有两个根 , 分别为 ( -1, 0 ) 和 ( 1,0 ).

当 n=3 时 , 它有三个根,  分别为

　　

那么推广 , 当有 n 次时 , 即有 n 个单位根.

 

 

那么,在复平面中的单位根是怎么表示的呢 ?

如图 n=5 , 5个红点即为 所有的单位根.

 

 

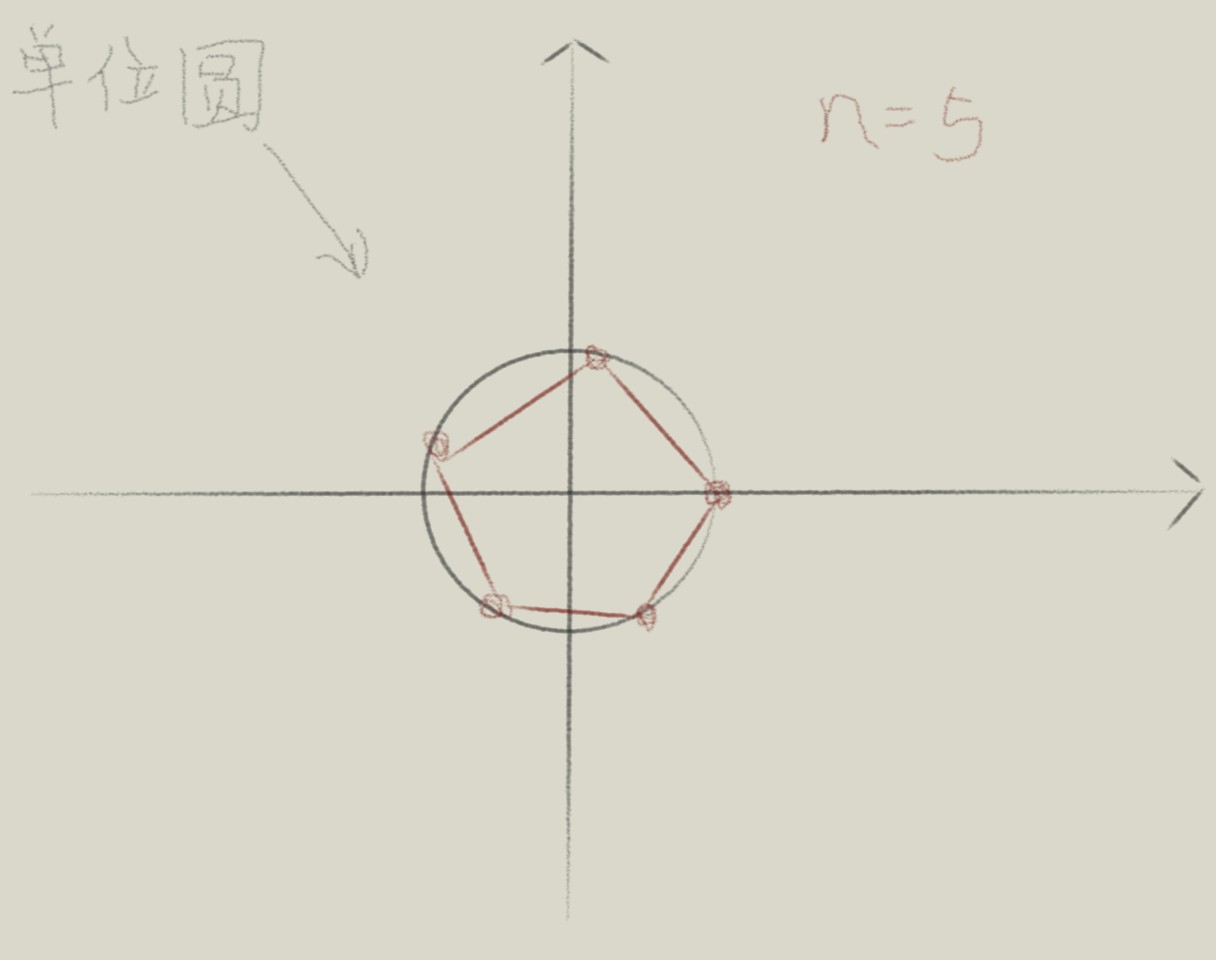
由此我们可以推出,单位根在复平面中的分布规律：

 

1.为 n 次方 就会把单位圆 分成 n 等分.

 

2.n 个点连起来即为一个 正 n 边形.

 

3.n 个点的起点即为 : ( 1,0 )

 

4.按照 360度 按 n 等分分 ,然后从起点开始移动.

 

 

 

然后还有另外一个概念:

 

本源根

 

简单来说,本源根,就是 关于 z 的方程 z^n=1 的一个根 z1 , 我们认为其为一个本源根 

 

当且仅当:

　　　　 z1 只有 n 次方 的运算结果为 1 .

 

如 :

  对于 n = 2 的情况来说,只有 ( -1, 0 ) 为其本源根.

  因为 在 n<=2 中 , ( 1 , 0 ) 的 1 次方 和 2 次方 也都为 1;

  所以 ( -1 , 0 ) 即为当 n=2 时的本源根.

 

其他的情况可以以此类推.