题目链接:传送门
题目大意:根据题目给你的二叉树先序遍历,后序遍历,输出有多少种二叉树满足这两种遍历方式。
题目思路:
首先我们要知道 先序遍历 是先遍历当前节点,然后遍历左子树,最后遍历右子树
中序遍历 是先遍历节点的左子树,然后是当前节点,最后遍历右子树
后序遍历 是先遍历左子树,再遍历右子树,最后遍历当前节点
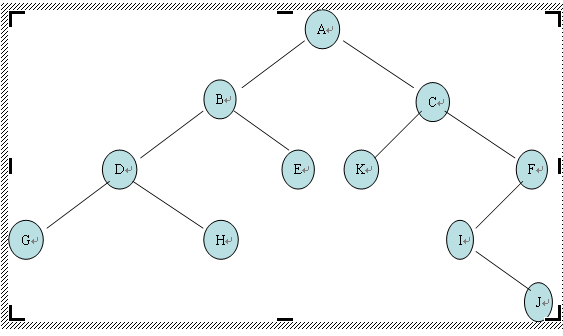
先序输出:
A B D G H E C K F I J
中序输出:
G D H B E A K C I J F
后序输出:
G H D E B K J I F C A
然后对于这个题来说,
我们要知道如果一个节点既有左子树又有右子树,那么这个节点在前序遍历和后序遍历的结果中就确定了
也就是只有一种结构。
如果一个节点只有左子树或者只有右子树,那么这个节点和他唯一的儿子节点就有两种结构满足相同的前序遍历和后序遍历(如题干)
这个题目要我们求有多少种满足情况的二叉树,也就是让我们找有多少个节点只有一个子节点
那么我们怎么来处理?
这里再次用到前序遍历和后续遍历的性质:一个节点和它唯一的子节点在前序遍历和后序遍历中出现的位置刚好相反(也就是反串),我们只要找到了
一个反串,也就找到了一个只有一个子节点的节点,记录符合条件的节点数n,然后答案就是2^n
#include <iostream> #include <cstdio> #include <cstdlib> #include <cmath> #include <algorithm> #include <cstring> #include <stack> #include <cctype> #include <queue> #include <string> #include <vector> #include <set> #include <map> #include <climits> #define lson root<<1,l,mid #define rson root<<1|1,mid+1,r #define fi first #define se second #define ping(x,y) ((x-y)*(x-y)) #define mst(x,y) memset(x,y,sizeof(x)) #define mcp(x,y) memcpy(x,y,sizeof(y)) using namespace std; #define gamma 0.5772156649015328606065120 #define MOD 1000000007 #define inf 0x3f3f3f3f #define N 2000005 #define maxn 100005 typedef pair<int,int> PII; typedef long long LL; int n,m,ans,dis[30],len; char str1[30],str2[30]; int main(){ int i,j,group,x,y,v,temp; scanf("%s",str1); scanf("%s",str2); len=strlen(str1); for(i=0;i<len;++i)dis[str2[i]-'a']=i; LL ans=1; for(i=0;i<len-1;++i){ int s1=str1[i]-'a',s2=str1[i+1]-'a'; if(dis[s1]-dis[s2]==1)ans<<=1; } printf("%lld ",ans); return 0; }