前言
至于为什么D2要分上下午,唯一的原因就是lyd那个毒瘤用了一上午讲他昨天要讲的鬼畜东西,所以今天下午才开始讲数论了
对了,补一下lyd的数论人
《数论人》(大雾) 数论的光束是歌德巴赫
那是谁?是谁?是谁? 将数论之力 集于一身
那是数论 数论人 数论人 正义的英雄
背负着纯粹数学之名 数论人 数论人
舍弃了一切(指实际生产)去战斗的男人
数论之箭是费马大定理
数论之耳是四色定理
数论之翼是黎曼猜想
开始吧
各种各样的高精
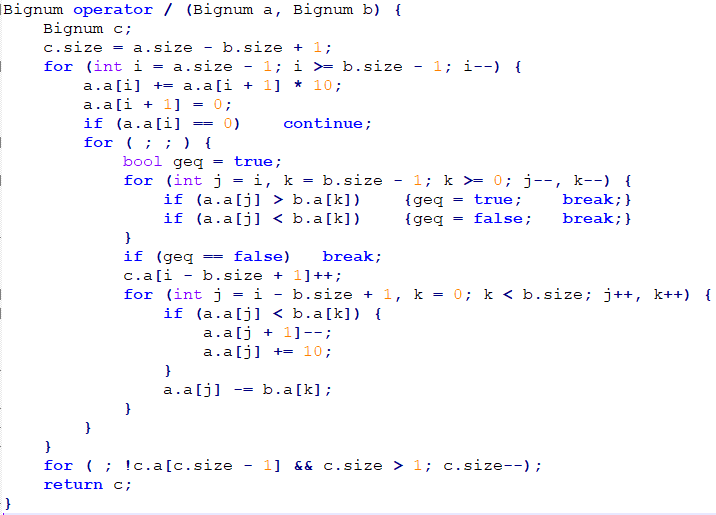
这个魔鬼上来就讲高精度
因为都学会了,就直接看当年的博客吧(惆怅
快速幂
这个其实是基于倍增思想?(反正很多东西都是相通的
其实就是/2下取整等等操作,代码如下
int power(int a, int p) {
long long res = 1;
while (p)
{
if (p & 1)
res = res * a;
a = a * a;
p >>= 1;
}
return res;
}
矩阵乘法
一个i行k列的矩阵乘上一个k行j列的矩阵会变成i行j列的矩阵
答案矩阵的第i,j个元素为A矩阵第i行第k个元素乘B矩阵第k行第j个元素,k是从1到m,就是一个矩阵的行乘另一个矩阵的列
上一下代码
for (int i = 1;i <= n; ++i)
for (int k = 1;k <= m; ++k)
for (int j = 1;j <= r;++j)
c[i][j] + a[i][k] * b[k][j];
矩阵乘法常常用于求一些线性的递归方程组,可以起到非常牛逼的加速作用
比如斐波那契的矩阵就是
1 1
1 0
[f[n], f[n - 1] ] * [矩阵] ^ k = [f[n + k], [n + k - 1] ]
矩阵快速幂基于以下的原理,即可以找到一个矩阵 M使得
[F(n-1) F(n)]T * M = [F(n) F(n+1)] T
以斐波拉期数列为例:M = ((1 1) (1 0))
以此类推:
[F(0) F(1)]T * Mn = [F(n) F(n+1)]T
我们成功将一个递推式转化成了一个求矩阵幂的问题
利用快速幂算法可以将时间缩短为 O(d^3 logn)
利用 FFT + 矩阵特征多项式的黑科技可以把时间进一步缩短到 O(dlogdlogn)
我们来试着写一下下面的矩阵:
F(n) = 7F(n-1) + 6F(n-2) + 5n + 4 * 3^n
先考虑转换前后的两个矩阵,肯定要有所有在转换中需要的
我们发现如果要从f[n-1]转换到f[n],要用到f[n-1],f[n-2],n,3^n,我们就先写上这些
然后发现n要转换到n+1就需要个1,再加上1就好了
[f[n - 1], f[n - 2], n, 3 ^ n, 1]
[f[n], f[n - 1], n + 1, 3 ^ (n + 1) ,1]
然后按照递推式搞一搞就ok
高斯消元
这个东西和行列式求值也比较像,其实就是用矩阵运算吧
这是曾经的一个代码
#include <iostream>
#include <string>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
double n, a[20][20], ans = 1;
int sum;
inline void CH1(int x, int y, double k) //第y行减k*x
{
for (int i = 1; i <= n; ++i)
a[y][i] -= (double)(k * a[x][i]);
}
inline void CH2(int x, int y) //交换x列和y列
{
for (int i = 1; i <= n; ++i)
swap(a[i][x], a[i][y]);
}
inline double CH3(int x, double k) //把第x行提出一个公因数k
{
for (int i = 1; i <= n; ++i)
a[x][i] /= k;
return k;
}
int main()
{
scanf("%lf", &n);
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
scanf("%lf", &a[i][j]);
for (int i = 1; i < n; ++i)
{
sum=i;
while (a[i][i] == 0 && sum<=n) //对是否a[i][i]是0的特判
{
CH2(i, sum + 1); //交换x列和y列
ans *= -1;
sum++;
}
ans *= CH3(i, a[i][i]);
for (int j = i + 1; j <= n; ++j)
CH1(i, j, a[j][i]);
}
for (int i = 1; i <= n; ++i)
ans *= a[i][i];
printf("%0.0lf", ans);
return 0;
}
这个是lh神仙的高斯消元
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pr;
const double pi = acos(-1);
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define per(i, n, a) for (int i = n; i >= a; i--)
#define Rep(i, u) for (int i = head[u]; i; i = Next[i])
#define clr(a) memset(a, 0, sizeof a)
#define pb push_back
#define mp make_pair
#define fi first
#define sc second
ld eps = 1e-9;
ll pp = 1000000007;
ll mo(ll a, ll pp)
{
if (a >= 0 && a < pp)
return a;
a %= pp;
if (a < 0)
a += pp;
return a;
}
ll powmod(ll a, ll b, ll pp)
{
ll ans = 1;
for (; b; b >>= 1, a = mo(a * a, pp))
if (b & 1)
ans = mo(ans * a, pp);
return ans;
}
ll read()
{
ll ans = 0;
char last = ' ', ch = getchar();
while (ch < '0' || ch > '9')
last = ch, ch = getchar();
while (ch >= '0' && ch <= '9')
ans = ans * 10 + ch - '0', ch = getchar();
if (last == '-')
ans = -ans;
return ans;
}
//head
int n, m;
double a[100][100];
bool check(int k)
{
if (fabs(a[k][n + 1]) < eps)
return 1;
rep(i, 1, n) if (fabs(a[k][i]) > eps) return 1;
return 0;
}
int main()
{
n = read();
m = n;
rep(i, 1, m)
rep(j, 1, n + 1) a[i][j] = read();
int flag = 0;
rep(i, 1, n)
{
int t = i;
while (a[t][i] == 0 && t <= n)
t += 1;
if (t == n + 1)
{
flag = 1;
continue;
}
rep(j, 1, n + 1) swap(a[i][j], a[t][j]); //交换两行
double kk = a[i][i]; //每一行对角线上的值
rep(j, 1, n + 1) a[i][j] /= kk;
rep(j, 1, m) //循环m个式子 开始消元
if (i != j)
{
double kk = a[j][i];
rep(k, 1, n + 1)
a[j][k] -= kk * a[i][k];
}
}
if (flag)
{
return printf("No Solution
"), 0;
}
rep(j, 1, m)
{
printf("%.2lf", a[j][n + 1] / a[j][j]);
puts("");
}
return 0;
}
数论好恶心
筛法
筛法的话一般就是埃拉托色尼筛或者是欧拉筛(线性筛)
埃拉托色尼筛
思想就是所有质数的倍数都被筛掉
memset(b, false, sizeof(b));
int tot = 0;
for (int i = 2; i <= n; ++i)
{
if (!b[i])
{
prime[++tot] = i;
for (int j = i * 2; j <= n; j += i)
b[j] = true;
}
}
欧拉筛(线性筛)
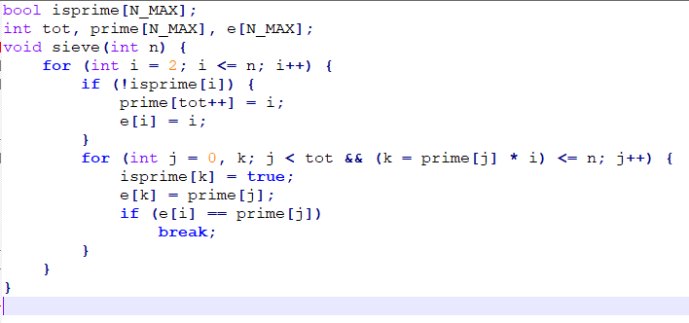
保证了所有的数只被最小的质因数筛掉
欧拉筛还可以用来维护一些复杂的函数值
如:逆元、一个数的质因数分解中最大的指数的值
积性函数
积性函数:对于所有互质的 x 和 y,F(x * y) = F(x) * F(y)
完全积性函数:对于所有 x 和 y ,F(x * y) = F(x) * F(y)
常见的积性函数:
欧拉函数 φ(n) :不超过 n 与 n 互素的数的个数
若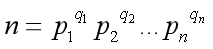 则
则