打总结啊打总结。。。
自己今天还是智障了24小时哦~
1、
Ib的沙漏(hourglass)
正当Ib欣赏着一副诡异的画时,大厅的灯闪烁了几下,便熄灭了
墙上流出了蓝色的液体,上面写着……xxxxx
Ib满怀着恐惧的走出大厅,发现整个美术馆已经空无一人,大门紧锁,灯光也暗淡了下来,正当她感到无望时,她想起了自己的神奇沙漏,这个沙漏由n个小沙漏组成,第i个小沙漏的沙子数量为ai,这个沙漏有一个神奇的性质,如果用手拨动第i个小沙漏,这个沙漏的沙子数量会变成sqrt(ai)(向下取整),Ib经常玩弄她的沙漏以打发时间,有时她会用手连续拨动第l到r个小沙漏,有时她会数第l到r个小沙漏的沙子数量之和为多少,可惜Ib今早把沙漏忘在家里了,希望你能帮她模拟一个沙漏,这样也许她就不会害怕了,额…
Input
第一行一个整数n
第二行n个整数a1,a2,…,an,(0<=ai<=10^9)
第三行一个整数m表示Ib玩弄沙漏的次数
接下来m行,每行三个整数t,l,r
若t=1表示Ib数第l到r个小沙漏的沙子数量之和
若t=2表示Ib拨动第l到r个小沙漏
Output
每次t=1时,每行一个整数,表示第l到r个小沙漏的沙子数量之和
Sample Input
4
1 100 5 5
5
1 1 2
2 1 2
1 1 2
2 2 3
1 1 4
Sample Output
101
11
11
数据范围:
30%:n,m<=1000
100%:n,m<=100000
对于>=1的数,根号的话,几次就会变成1了,变成1之后再根号也不会变,所以就对于>1的数,暴力修改,用树状数组维护。
维护连续的1的话就用并查集。
额。。骚年你还是没有考虑0的情况ORZ...

1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 #include<algorithm> 6 #include<cmath> 7 using namespace std; 8 #define Maxn 100010 9 #define LL long long 10 11 int a[Maxn],fa[Maxn]; 12 13 int ffa(int x) 14 { 15 if(fa[x]!=x) fa[x]=ffa(fa[x]); 16 return fa[x]; 17 } 18 19 LL c[Maxn]; 20 int n; 21 void add(int x,int y) 22 { 23 for(int i=x;i<=n;i+=i&(-i)) 24 c[i]+=y; 25 } 26 27 LL query(int l,int r) 28 { 29 LL ans=0; 30 for(int i=r;i>=1;i-=i&(-i)) 31 ans+=c[i]; 32 l--; 33 for(int i=l;i>=1;i-=i&(-i)) 34 ans-=c[i]; 35 return ans; 36 } 37 38 void init() 39 { 40 scanf("%d",&n); 41 for(int i=1;i<=n;i++) scanf("%d",&a[i]); 42 memset(c,0,sizeof(c)); 43 for(int i=1;i<=n;i++) add(i,a[i]); 44 for(int i=1;i<=n;i++) fa[i]=i; 45 for(int i=n-1;i>=1;i--) 46 { 47 if(a[i]==1&&a[i+1]==1) 48 { 49 fa[ffa(i)]=ffa(i+1); 50 } 51 } 52 } 53 54 void ffind() 55 { 56 int m; 57 scanf("%d",&m); 58 for(int i=1;i<=m;i++) 59 { 60 int opt,l,r,tt; 61 scanf("%d%d%d",&opt,&l,&r); 62 if(l>r) tt=l,l=r,r=tt; 63 if(opt==1) 64 { 65 printf("%lld ",query(l,r)); 66 } 67 else 68 { 69 for(int j=l;j<=r;) 70 { 71 if(a[j]!=1) 72 { 73 int nn=a[j]; 74 a[j]=(int)sqrt((double)a[j]); 75 add(j,a[j]-nn); 76 if(a[j]==1) 77 { 78 if(a[j+1]==1) fa[ffa(j)]=ffa(j+1); 79 if(a[j-1]==1) fa[ffa(j-1)]=ffa(j); 80 } 81 j++; 82 } 83 else 84 { 85 j=ffa(j)+1; 86 } 87 } 88 } 89 } 90 } 91 92 int main() 93 { 94 init(); 95 ffind(); 96 return 0; 97 }
2、
诡异的雕塑(sculpture)
玩腻了沙漏的Ib决定勇敢地前进,她走进了一幅画中,来到了画中的世界!额… 在这里她遇到了与自己一样迷失在画中的Garry,
于是他们决定结伴而行,继续在画中的世界探索。
他们来到了一个绿色房间,这个房间没有出口,只有一排诡异的雕塑,聪明的Ib一看就知道要怎么做了,这里一共有n个雕塑,第i个雕塑的高度位hi,只要把这些雕塑摆成类似于一个山峰的形状就行了,具体地说,存在i使得对于1<=j<i,h[j]<=h[j+1], 对于i<j<=n,h[j-1]>=h[j],摆成这样后,房间的,们就会自动打开,当然Ib可搬不动这些雕塑,她只能向Garry求助,Garry每次只能交换相邻的两个雕塑,为了帮Garry节省力气继续后面的闯关,请你求出最少的交换次数。
Input
第一行一个正整数n
接下来n行,第i行一个整数hi
Output
输出一个整数,表示Garry最少需要的交换次数
Sample Input
6
2
8
4
5
3
6
Sample Output
3
HINT
最终的高度序列为2 4 5 8 6 3,共需要操作三次。
3<=n<=3*10^5
1<=hi<=10^9
数据范围
30% n<=10
100% n<=300000
额。。。无语,j打成了i错过了AC这题的机会。。。
就是权值从小到大枚举,看看放在最左边好还是最右边好,然后把这个数删掉。
注意数值相同的情况就好了。

1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 #include<algorithm> 6 using namespace std; 7 #define Maxn 300010 8 #define LL long long 9 10 LL h[Maxn]; 11 12 struct node 13 { 14 LL x,id; 15 }t[Maxn]; 16 17 bool cmp(node x,node y) {return x.x<y.x;} 18 19 LL mymin(LL x,LL y) {return x<y?x:y;} 20 21 LL c[Maxn]; 22 LL n; 23 LL add(LL x,LL y) 24 { 25 for(LL i=x;i<=n;i+=i&(-i)) 26 c[i]+=y; 27 } 28 29 LL query(LL x) 30 { 31 LL ans=0; 32 for(LL i=x;i>=1;i-=i&(-i)) 33 ans+=c[i]; 34 return ans; 35 } 36 37 int main() 38 { 39 scanf("%lld",&n); 40 for(LL i=1;i<=n;i++) scanf("%lld",&h[i]); 41 for(LL i=1;i<=n;i++) 42 { 43 t[i].id=i,t[i].x=h[i]; 44 } 45 sort(t+1,t+1+n,cmp); 46 memset(c,0,sizeof(c)); 47 for(LL i=1;i<=n;i++) add(i,1); 48 LL ans=0; 49 for(LL i=1;i<=n;) 50 { 51 LL r=i;add(t[i].id,-1); 52 while(t[r+1].x==t[i].x&&r<n) 53 { 54 r++; 55 add(t[r].id,-1); 56 } 57 for(LL j=i;j<=r;j++) 58 { 59 ans+=mymin(query(t[j].id-1),n-r-query(t[j].id-1)); 60 } 61 i=r+1; 62 } 63 printf("%lld ",ans); 64 return 0; 65 }
3、
Mary的游戏(game)
继续前进Ib和Garry又遇见了迷失在画中的世界里的Mary(左)
现在Mary被一个游戏难住了,没有玩出这个游戏Mary就不走了,可是以Mary的智商恐怕很难通关,为了尽快逃离这个地方,请你这帮Mary通关吧
Mary有一个n*m的矩形卡片,每个格子有权值Aij,每条边有权值,现在Mary要求一个联通块,使得格子的权值Aij/联通块边界上的边的权值之和最大。具体见样例
Input
第一行为两个正整数n,m。
接下来n行,每行m个非负整数,表示对应格子的价值。
接下来n+1行,每行m个正整数,表示所有横向的格线上的费用。
接下来n行,每行m+1个正整数,表示所有纵向的格线上的费用。
(所有数据均按从左到右,从上到下的顺序输入,参见样例和配图)
Output
输出一行仅含一个数,表示最大的V/C,保留3位小数。
Sample Input
3 4
1 3 3 3
1 3 1 1
3 3 1 0
100 1 1 1
97 96 1 1
1 93 92 92
1 1 90 90
98 1 99 99 1
95 1 1 1 94
1 91 1 1 89
Sample Output
1.286
HINT
数据范围 30% n,m<=5 100% n,m<=50
啊。。智障!!!!!【我说我智障
想了好久不连通怎么破。。。想不到。。。
跟海岸线那题像极,首先是0-1分数规划,先二分mid,然后让w-mid*l>=0
然后就是让w-MID*L最大,不连通也没关系,因为几个联通块的w-mid*l>=0,那么肯定每一个都是w-mid*l>=0。【就是这里想不到呀!!是不是傻= =
so...........
最小割直接上ORZ。。。【其实中间是判断>0而不是>=0,因为不能什么都不选ORZ。。。

1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 #include<algorithm> 6 #include<queue> 7 using namespace std; 8 #define Maxn 60 9 #define INF 0xfffffff 10 11 int w[Maxn][Maxn],w1[Maxn][Maxn],w2[Maxn][Maxn]; 12 13 struct node 14 { 15 int x,y,next,o; 16 double f; 17 }t[Maxn*Maxn*100];int len; 18 int first[Maxn*Maxn*10]; 19 20 void ins(int x,int y,double f) 21 { 22 if(f==0) return; 23 t[++len].x=x;t[len].y=y;t[len].f=f; 24 t[len].next=first[x];first[x]=len;t[len].o=len+1; 25 t[++len].x=y;t[len].y=x;t[len].f=0; 26 t[len].next=first[y];first[y]=len;t[len].o=len-1; 27 } 28 29 // int mymin(int x,int y) {return x<y?x:y;} 30 double mymin(double x,double y) {return x<y?x:y;} 31 32 double sum,sl; 33 int n,m; 34 void init() 35 { 36 scanf("%d%d",&n,&m); 37 sum=0;sl=0; 38 for(int i=1;i<=n;i++) 39 for(int j=1;j<=m;j++) 40 { 41 scanf("%d",&w[i][j]); 42 sum+=w[i][j]; 43 } 44 for(int i=0;i<=n;i++) 45 for(int j=1;j<=m;j++) 46 { 47 scanf("%d",&w1[i][j]); 48 sl+=w1[i][j]; 49 } 50 for(int i=1;i<=n;i++) 51 for(int j=0;j<=m;j++) 52 { 53 scanf("%d",&w2[i][j]); 54 sl+=w2[i][j]; 55 } 56 } 57 58 int num[Maxn][Maxn],cnt; 59 int st,ed; 60 queue<int > q; 61 int dis[Maxn*Maxn*10]; 62 bool bfs() 63 { 64 while(!q.empty()) q.pop(); 65 memset(dis,-1,sizeof(dis)); 66 dis[st]=0;q.push(st); 67 while(!q.empty()) 68 { 69 int x=q.front(); 70 for(int i=first[x];i;i=t[i].next) if(t[i].f>0) 71 { 72 int y=t[i].y; 73 if(dis[y]==-1) 74 { 75 dis[y]=dis[x]+1; 76 q.push(y); 77 } 78 } 79 q.pop(); 80 } 81 if(dis[ed]==-1) return 0; 82 return 1; 83 } 84 85 double ffind(int x,double flow) 86 { 87 if(x==ed) return flow; 88 double now=0; 89 for(int i=first[x];i;i=t[i].next) if(t[i].f>0) 90 { 91 int y=t[i].y; 92 if(dis[y]==dis[x]+1) 93 { 94 double a=ffind(y,mymin(t[i].f,flow-now)); 95 t[i].f-=a; 96 t[t[i].o].f+=a; 97 now+=a; 98 } 99 if(now==flow) break; 100 } 101 if(now==0) dis[x]=-1; 102 return now; 103 } 104 105 double max_flow() 106 { 107 double ans=0; 108 while(bfs()) 109 { 110 ans+=ffind(st,INF); 111 } 112 return ans; 113 } 114 115 int fa[Maxn]; 116 117 void output() 118 { 119 /*for(int i=1;i<=cnt+2;i++) 120 for(int j=first[i];j;j=t[j].next) if(t[j].f!=0) 121 printf("%d->%d %lf ",t[j].x,t[j].y,t[j].f);*/ 122 for(int i=1;i<=len;i+=2) 123 printf("%d->%d %lf ",t[i].x,t[i].y,t[i].f); 124 125 printf(" "); 126 } 127 128 bool check(double mid) 129 { 130 len=0; 131 memset(first,0,sizeof(first)); 132 cnt=0; 133 for(int i=1;i<=n;i++) 134 for(int j=1;j<=m;j++) num[i][j]=++cnt; 135 st=cnt+1;ed=st+1; 136 for(int i=1;i<n;i++) 137 for(int j=1;j<=m;j++) 138 { 139 ins(num[i][j],num[i+1][j],w1[i][j]*mid); 140 ins(num[i+1][j],num[i][j],w1[i][j]*mid); 141 } 142 for(int i=1;i<=n;i++) 143 for(int j=1;j<m;j++) 144 { 145 ins(num[i][j],num[i][j+1],w2[i][j]*mid); 146 ins(num[i][j+1],num[i][j],w2[i][j]*mid); 147 } 148 for(int i=1;i<=n;i++) 149 for(int j=1;j<=m;j++) 150 { 151 ins(st,num[i][j],0); 152 ins(num[i][j],ed,w[i][j]); 153 } 154 for(int i=1;i<=m;i++) 155 { 156 ins(st,num[1][i],w1[0][i]*mid); 157 ins(st,num[n][i],w1[n][i]*mid); 158 } 159 for(int i=1;i<=n;i++) 160 { 161 ins(st,num[i][1],w2[i][0]*mid); 162 ins(st,num[i][m],w2[i][m]*mid); 163 } 164 // printf("%lf ",mid); 165 // output(); 166 double x=sum-max_flow(); 167 // double x=get_ans(); 168 return x>0; 169 } 170 171 void ffind() 172 { 173 double l=0,r=sum; 174 while(r-l>0.0001) 175 { 176 double mid=(l+r)/2; 177 if(check(mid)) l=mid; 178 else r=mid; 179 } 180 printf("%.3lf ",l); 181 } 182 183 int main() 184 { 185 init(); 186 ffind(); 187 return 0; 188 }
4、
拯救Mary(save)
在经历了无数艰难险阻之后…
Ib和Garry发现Mary竟然不是真人!她只是美术馆的一幅画,在Ib和Garry得知真相后,Mary准备攻击Ib和Garry,Ib和Garry只能狠下心来将Mary的画烧了
然而Ib和Garry都很后悔,希望找到方法可以复活Mary,聪明的Ib又想到了办法,她将Mary的画的碎片收集了起来,每张碎片都是一棵n个节点的树,但是有一些节点是特殊节点,且特殊节点两两不相邻,如果找出有多少种不同(树可以任意转动)的碎片就可以复活Mary啦 (详见样例)
Input
第一行为一个正整数n
接下来n-1行,每行2个整数x,y表示一条树边
Output
输出一个数,表示有多少种不同的碎片
Sample Input
5
1 2
1 3
1 4
1 5
Sample Output
6
HINT
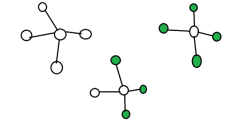
以下为6种情况
数据范围
20% n<=1000,树为一条链
100% n<=500000
这题好难啊不会做ORZ。。
首先,找到树的重心,(它不可能被其他不是重心的孩子代替,
而且,树最多两个重心【并且连在一起,为什么自己想吧。。大神说这很明显??
然后差不多就是树形DP部分,
先算孩子的,然后判断两棵子树是否完全相等,相等就要算重复排列。。。
判断子树是否完全相等要用HASH【ORZ。。。
我不会打,没代码= =
2016-11-11 19:35:21