寒假 杂题题解

寒假 杂题题解

大根堆

题意

从一棵树上选出尽可能多的点，满足大根堆性质

即对于 \(i,j\) 若 \(j\) 是 \(i\) 是 \(j\) 的祖先，则 \(v_i>v_j\)，\(v\) 为点权

这些点不必形成这棵树的一个连通子树。\(n\le2\times10^5\)

sol

由于点不需要相邻，这题其实是树上 LIS ，

考虑维护 \(n\log n\) 求 LIS 时的那个数组，可以用 multiset 解决

对每个点开一个这样的 multiset 维护子树中的值，

向上时合并两个 multiset，启发式合并复杂度为 \(O(n\log^2n)\)

code

#include <bits/stdc++.h>
#define pb push_back
using namespace std;
typedef unsigned long long uLL;
typedef long double LD;
typedef long long LL;
typedef double db;
const int N = 200005;
int n, a[N];
vector<int> G[N];
multiset<int> s[N];
typedef multiset<int>::iterator iter;
inline void mer(int x, int y) {
    if (s[x].size() < s[y].size())
        swap(s[x], s[y]);
    for (iter it = s[y].begin(); it != s[y].end(); it++) s[x].insert(*it);
}
void dfs(int u) {
    for (int i = 0, v, le = G[u].size(); i < le; i++) dfs(v = G[u][i]), mer(u, v);
    iter it = s[u].lower_bound(a[u]);
    if (it != s[u].end())
        s[u].erase(it);
    s[u].insert(a[u]);
}
int main() {
    scanf("%d", &n);
    for (int i = 1, y; i <= n; i++) {
        scanf("%d%d", &a[i], &y);
        if (y)
            G[y].pb(i);
    }
    dfs(1);
    printf("%d", s[1].size());
}

排队

题意

\(n\) 个人编号为 1 到 \(n\)，现在需要按编号升序排序，有 3 种操作

• 花费 \(A_i\) 将编号为 \(i\) 的移动到任意位置
• 花费 \(B_i\) 将编号为 \(i\) 的移动到最左边
• 花费 \(C_i\) 将编号为 \(i\) 的移动到最右边

给出初始排列，最小化代价，\(n\le2\times 10^5\)

sol

至少有 1 人不用移动，设 \(f_i\) 为小于等于 \(i\) 的编号都排好序且编号 \(i\) 的人没有移动，时的最小花费

\(pos_i\) 为编号 \(i\) 的初始位置

\[f_i=\min(\sum_{j=1}^{i-1}\min(A_j,B_j), \quad\min_{j<i\and pos_j<pos_i} f_j+\sum_{k=j+1}^{i-1}A_k) \]

答案为

\[\min_{1\le i\le n}f_i+\sum_{i<j\le n} \min(A_j,C_j) \]

可以用线段树优化，即记 \(A\) 的前缀和为 \(s\) ，可得

\[\begin{aligned} &\min f_j+\sum_{k=j+1}^{i-1}A_k \\ &=\min f_j+s_{i-1}-s_j \\ &=s_{i-1}+\min f_j-s_j \end{aligned} \]

区间 \([l,r]\) 维护编号在 \([l,r]\) 中的 \(f_j-s_j\) 的最小值

code

#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long uLL;
typedef long double LD;
typedef long long LL;
typedef double db;
const int N = 200005;
int n, x[N];
LL A[N], B[N], C[N], f[N];
LL s2[N], s[N], ans, mn[N << 2], res;
struct seg {
    int l, r;
} T[N << 2];
#define ls (rt << 1)
#define rs (rt << 1 | 1)
inline void Up(int rt) { mn[rt] = min(mn[ls], mn[rs]); }
void bui(int l, int r, int rt) {
    T[rt].l = l, T[rt].r = r;
    mn[rt] = 1e15;
    if (l == r)
        return;
    register int mid = l + r >> 1;
    bui(l, mid, ls), bui(mid + 1, r, rs);
}
void mdy(int p, LL v, int rt = 1) {
    if (T[rt].l == T[rt].r) {
        mn[rt] = v;
        return;
    }
    if (p <= T[ls].r)
        mdy(p, v, ls);
    else
        mdy(p, v, rs);
    Up(rt);
}
void ask(int ql, int qr, int rt = 1) {
    if (qr < T[rt].l || T[rt].r < ql)
        return;
    if (ql <= T[rt].l && T[rt].r <= qr) {
        res = min(res, mn[rt]);
        return;
    }
    ask(ql, qr, ls), ask(ql, qr, rs);
}
#undef ls
#undef rs
int main() {
    scanf("%d", &n);
    for (int i = 1, a; i <= n; i++) scanf("%d", &a), x[a] = i;
    for (int i = 1; i <= n; i++) {
        scanf("%lld%lld%lld", &A[i], &B[i], &C[i]);
        s[i] = s[i - 1] + A[i];
        s2[i] = s2[i - 1] + min(A[i], C[i]);
    }
    bui(1, n, 1);
    register LL ss = 0;
    for (int i = 1; i <= n; i++) {
        f[i] = ss, ss += min(A[i], B[i]);
        res = 1e15;
        ask(1, x[i] - 1);
        f[i] = min(f[i], res + s[i - 1]);
        mdy(x[i], f[i] - s[i]);
    }
    ans = 1e15;
    for (int i = 1; i <= n; i++) ans = min(ans, f[i] + s2[n] - s2[i]);
    printf("%lld", ans);
}

黑球与白球

题意

\(n\) 个白球和 \(m\) 个黑球摆成一行，从左到右，需满足：

• 设 \(w_i,b_i\) 分别表示前 \(i\) 个球中白球、黑球的数量，对于任意位置 \(i\) 有 \(w_i\le b_i+K\)

求方案数 \(n,m\le 10^6\)

sol

放到坐标系里，则是从原点 \(O\) 不经过直线 \(y=x+K\) 到点 \((M,N)\) 的方案数

总方案数为 \(C_{n+m}^n\) ，考虑不合法的方案数

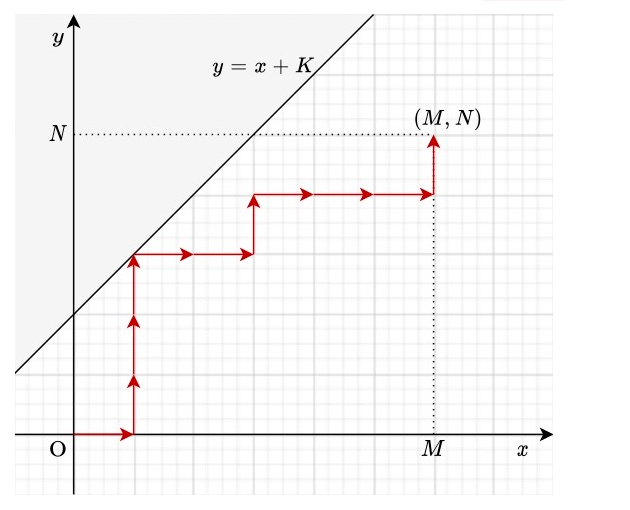
原点 \(O\) 关于 \(y=x+K+1\) 对称点 \(O'\) ，则从 \(O'\) 到点 \(M,N\) 的所有路径都是不合法的

为 \(C_{n+m}^{n-K-1}\)

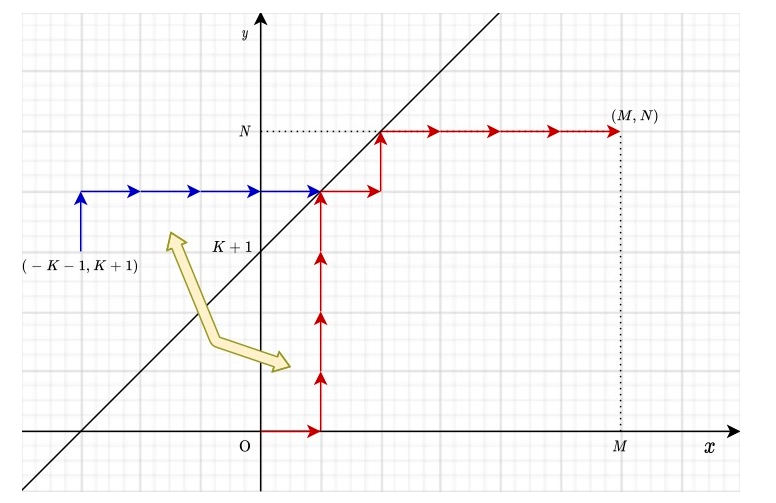
故答案为 \(C_{n+m}^n-C_{n+m}^{n-K-1}\)

code

#include <bits/stdc++.h>
using namespace std;
const int N = 2000005;
typedef long long LL;
const LL P = 1e9 + 7;
inline LL Pow(LL x, LL y) {
    register LL res = 1;
    for (; y; y >>= 1, x = x * x % P)
        if (y & 1)
            res = res * x % P;
    return res;
}
int n, m, K;
LL fac[N], inv[N];
inline LL C(int n, int m) {
    if (n == m || m == 0)
        return 1;
    if (n < m || m < 0)
        return 0;
    return fac[n] * inv[m] % P * inv[n - m] % P;
}
int main() {
    scanf("%d%d%d", &n, &m, &K);
    if (n > m + K)
        return puts("0"), 0;
    fac[0] = 1;
    for (int i = 1; i <= n + m; i++) fac[i] = fac[i - 1] * i % P;
    inv[n + m] = Pow(fac[n + m], P - 2);
    for (int i = n + m - 1; i >= 1; i--) inv[i] = inv[i + 1] * (i + 1) % P;
    printf("%lld", (C(n + m, n) - C(n + m, n - K - 1) + P) % P);
}

满足要求的排列个数

题意

求 \(1,2,\cdots,n\) 组成的满足要求的排列 \(a\) 的数量：

• \(\forall 1\le i\le m\) 。\(a\) 的前 \(x_i\) 个元素中最多只能有 \(z_i\) 个元素小于等于 \(y_i\)

\(n\le 18,m\le100\)

sol

显然状压，设 \(f[S]\) 为前面的 \(|S|\) 个元素与集合 \(S\) 吻合的合法排列数

对所有条件按 \(x_i,y_i\) 储存，放在 \(a[x_i][y_i]\) 中

计算 \(S\) 中 1 的个数 \(cnt\) ，检测是否满足条件 \(a[cnt][Y_i]\) ，不符合则 \(f[S]=0\)

否则 \(f[S]=\sum_{j\in S} f[S-j]\)

复杂度 \(O(2^n\times n)\)

code

#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long uLL;
typedef long double LD;
typedef long long LL;
typedef double db;
const int N = 20;
int n, m, a[N][N], mx;
LL f[1 << N];
int main() {
    scanf("%d%d", &n, &m);
    memset(a, 0x3f, sizeof(a));
    for (int i = 1, x, y, z; i <= m; i++) {
        scanf("%d%d%d", &x, &y, &z);
        a[x][y] = min(a[x][y], z);
    }
    mx = (1 << n) - 1;
    f[0] = 1;
    for (int i = 1, cnt, tt, fl; i <= mx; i++) {
        cnt = 0, tt = i;
        while (tt) ++cnt, tt -= tt & -tt;
        tt = 0, fl = 1;
        for (int j = 0; j < n; j++) {
            if ((i >> j) & 1)
                ++tt;
            if (tt > a[cnt][j + 1]) {
                fl = 0;
                break;
            }
        }
        if (!fl)
            continue;
        for (int j = 0; j < n; j++)
            if ((i >> j) & 1)
                f[i] += f[i ^ (1 << j)];
    }
    printf("%lld", f[mx]);
}

约数个数

题意

求 \(\binom{n}{k}\) 的约数个数 \(\mod 998244353\) ，\(n\le10^{12},k\le\min(10^6,n)\)

sol

\(\binom{n}{k}=\dfrac{n^{\underline{k}}}{k}\) ，其中 \(n^{\underline{k}}=n*(n-1)*\cdots*(n-k+1)\)

对分子分母共同分解质因数，用小学奥数即可求出答案。

考虑分子

筛出 \(\sqrt{n}\) 以内的质因数，最多 \(\dfrac{\sqrt{n}}{\ln\sqrt{n}}\) 个

用质数 \(p\) 去除 \([n-k+1,n]\) 中 \(p\) 的倍数，

最多有 \(\dfrac{K}{p}\) 个倍数，总共 \(\sum_p \dfrac{K}{p}<K*\ln\sqrt{n}\)

除完以后剩下的位置就是最后一个大质因数，

一个位置最多除 \(\log n\) 次，复杂度为 \(O(K\log n\ln\sqrt{n})\)

分母同理。

code

#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long uLL;
typedef long double LD;
typedef long long LL;
typedef double db;
const int N = 1e6 + 5;
const LL P = 998244353;
LL n, L, a[N], st, ans = 1;
int K, vis[N], pr[80000], cnt, sq, t[80000];
int main() {
    for (int i = 2; i <= 1e6; i++) {
        if (!vis[i]) pr[++cnt] = i;
        for (int j = 1; j <= cnt && i * pr[j] <= 1e6; j++) {
            vis[i * pr[j]] = 1;
            if (i % pr[j] == 0) break;
        }
    }
    scanf("%lld%d", &n, &K);
    sq = sqrt(n);
    st = n - K + 1;
    for (int i = 1; i <= K; i++) a[i] = st + i - 1;
    for (int i = 1, x; i <= cnt; i++) {
        x = pr[i];
        L = x * ((st - 1) / x + 1);
        for (LL j = L; j <= n; j += x)
            while (a[j - st + 1] % x == 0)
                ++t[i], a[j - st + 1] /= x;
    }
    sort(a + 1, a + K + 1);
    int tt = 0;
    for (int i = 1; i <= K; i++) {
        if (a[i] < 2) continue;
        if (a[i] ^ a[i + 1]) ans = ans * (tt + 1) % P, tt = 1;
        else ++tt;
    }
    if (a[K] > 1) ans = ans * (tt + 1) % P;
    for (int i = 1; i <= K; i++) a[i] = i;
    for (int i = 1, x; i <= cnt; i++) {
        x = pr[i];
        for (LL j = x; j <= K; j += x)
            while (a[j] % x == 0)
                --t[i], a[j] /= x;
    }
    for (int i = 1; i <= cnt; i++) ans = ans * (t[i] + 1) % P;
    printf("%lld", ans);
}

字符串

题意

有一个字符串，最多出现 'K','E','Y' 三种字母。

每次可以交换相邻的两个字符。问在不超过K次交换操作下，最多能得到多少个不同的字符串。

\(|S|\le 30,K\le 10^9\)

sol

逆序对最多 \(\dfrac{1}{2}n(n-1)\) 个，从此突破

设 \(f_{i,j,k,p}\) 为用了 \(i\) 个 'K' ，\(j\) 个 'E' ，\(k\) 个 'Y' 时逆序对有 \(p\) 个的字符串数

可从用不用当前字符，得到新增你逆序对个数，刷表

枚举最终可能逆序对个数，累加得到答案

code

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 35;
int K, p1[N], p2[N], p3[N], l1, l2, l3, n, Mx, tt;
LL f[N][N][N][505], ans;
char a[N];
inline void nx(int i, int j, int k, int p) {
    tt = 0;
    for (int l = 0; l < i; l++) tt += p1[l] > p;
    for (int l = 0; l < j; l++) tt += p2[l] > p;
    for (int l = 0; l < k; l++) tt += p3[l] > p;
}
int main() {
    scanf("%s%d", a + 1, &K);
    n = strlen(a + 1);
    Mx = n * (n - 1) / 2;
    for (int i = 1; i <= n; i++) {
        if (a[i] == 'K')
            p1[l1++] = i;
        if (a[i] == 'E')
            p2[l2++] = i;
        if (a[i] == 'Y')
            p3[l3++] = i;
    }
    f[0][0][0][0] = 1;
    for (int i = 0; i <= l1; i++)
        for (int j = 0; j <= l2; j++)
            for (int k = 0; k <= l3; k++)
                for (int p = 0; p < Mx; p++) {
                    if (i < l1) {
                        nx(i, j, k, p1[i]);
                        f[i + 1][j][k][p + tt] += f[i][j][k][p];
                    }
                    if (j < l2) {
                        nx(i, j, k, p2[j]);
                        f[i][j + 1][k][p + tt] += f[i][j][k][p];
                    }
                    if (k < l3) {
                        nx(i, j, k, p3[k]);
                        f[i][j][k + 1][p + tt] += f[i][j][k][p];
                    }
                }
    for (int i = 0; i <= min(K, Mx); i++) ans += f[l1][l2][l3][i];
    printf("%lld", ans);
}

区间游戏

题意

\(n\) 个区间 \([L_i,R_i)\) ，A 与 B 玩游戏，A 先来，每次从 \(n\) 个区间中选出一个，

且不能与之前选中取间有重叠，如果无法再选则另一玩家胜，问最后谁会赢，多组数据

\(n,L_i,R_i\le 100, T\le20\)

sol

设 \(f_{X,Y}=\) 在区间 \([X,Y)\) 玩游戏的 Grundy 数

可以用记忆化实现，模拟选择一个区间导致的划分，

由 Grundy 数的定义求出 \(mex\) ，复杂度 \(O(TNS^2)\) ，\(S\) 为初始区间长度，即 100

足以解决次问题

code

#include <bits/stdc++.h>
using namespace std;
const int N = 205;
int n, Ti, a[N], b[N], f[N][N];
int SG(int l, int r) {
    if (f[l][r] != -1)
        return f[l][r];
    int vis[N];
    memset(vis, 0, sizeof(vis));
    for (int i = 1; i <= n; i++)
        if (l <= a[i] && b[i] <= r)
            vis[SG(l, a[i]) ^ SG(b[i], r)] = 1;
    for (int i = 0;; i++)
        if (!vis[i]) {
            f[l][r] = i;
            break;
        }
    return f[l][r];
}
int main() {
    scanf("%d", &Ti);
    while (Ti--) {
        scanf("%d", &n);
        for (int i = 1; i <= n; i++) scanf("%d%d", &a[i], &b[i]);
        memset(f, -1, sizeof(f));
        if (SG(1, 100))
            puts("Alice");
        else
            puts("Bob");
    }
}