http://poj.org/problem?id=1743
这题是一道后缀数组的经典例题:求不可重叠最长重复子串。
题意:
有N(1 <= N <=20000)个音符的序列来表示一首乐曲,每个音符都是1..88范围内的整数,现在要找一个重复的主题。“主题”是整个音符序列的一个子串,它需要满足如下条件:
1.长度至少为5个音符。
2.在乐曲中重复出现。(可能经过转调,“转调”的意思是主题序列中每个音符都被加上或减去了同一个整数值)
3.重复出现的同一主题不能有公共部分。
题解:
因为可能同时加上或减去一个数,所以首先要作差比较。将后一个数减去前一个数得到新的数列c。
注意:例如1 2 3 4 5 2 3 4 5 6 变为 1 1 1 1 1 -3 1 1 1 1 ,重复子串的第一位是会变化的,最后要+1。
二分重复子串的长度k,然后判断它是否可行。
截自论文的图:
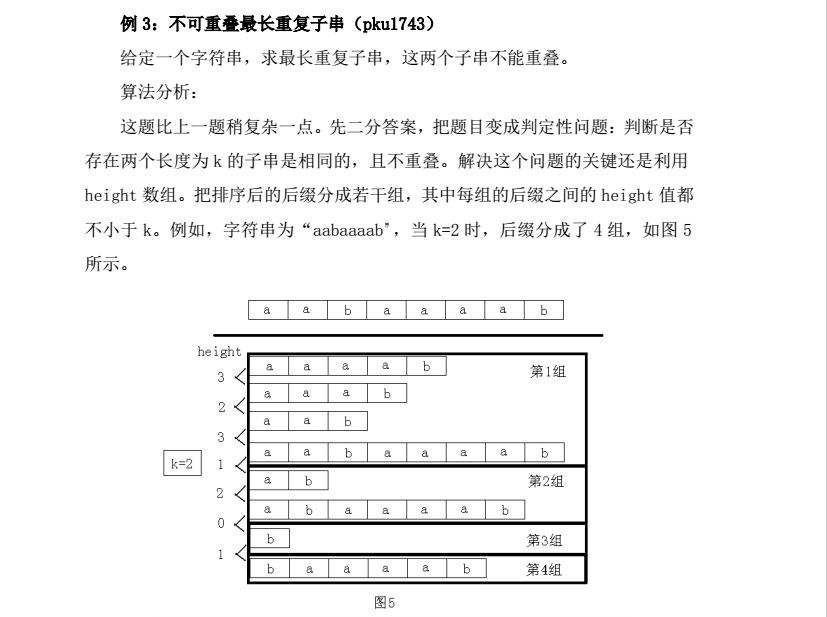

注意(我打的时候犯的错误):
1.分组的时候忽略了最后一组的判断。
2.因为判断的重复子串长度比真实长度小1,所以要判断位置x-y>k而不是>=k
对于这个问题的一组debug数据:1 2 3 4 5 1 2 3 4 5 1 ans=5
3.rk[i]不能等于0,至少>=1,因为我的模板没有第二关键字的那些的rk补成0了
4.看到评论里很多人犯了的错误:k最少是5,否则输出0
贴几组数据(debug好帮手):
input:
12
1 2 3 4 5 6 7 8 9 10 11 12
0
11
1 1 1 1 1 1 1 1 1 1 1
9
1 1 1 1 1 1 1 1 1
11
1 2 3 5 4 1 2 3 5 4 1
33
3 2 1 1 2 1 2 3 2 2 3 3 2 2 1 2 1 2 2 2 1 3 1 1 1 2 2 3 1 2 1 1 2
1
100
300
48 15 74 57 17 52 51 20 86 85 24 19 23 34 81 54 12 3 86 41 45 64 23 32 18 17 68 43 83 86
61 22 48 47 50 21 1 12 19 16 78 21 64 27 71 50 65 42 68 11 30 25 45 72 23 44 10 81 36 39
19 46 45 34 8 87 42 45 1 12 67 28 62 13 88 19 71 42 65 42 60 83 86 49 45 72 31 56 10 9
12 35 75 70 45 14 64 55 50 17 17 20 51 28 70 44 45 27 16 26 87 49 58 40 57 35 12 18 35
57 30 56 29 31 40 34 23 53 34 16 73 27 84 54 75 57 6 20 13 35 8 18 63 17 66 52 41 15 20
54 3 57 22 20 85 19 24 54 63 41 82 32 57 43 76 22 11 21 54 16 61 27 16 42 39 25 2 44 1
39 12 34 83 45 14 28 61 19 72 42 79 49 34 56 41 35 36 14 11 17 78 28 44 27 26 49 40 35
18 57 56 31 34 53 16 27 54 57 20 35 18 17 52 15 31 14 13 36 27 22 5 44 43 18 21 40 3 14
41 44 7 22 5 4 39 2 41 44 7 6 41 28 19 30 9 8 3 14 29 12 31 26 21 32 15 6 29 36 43 22 1
4 15 38 13 8 7 22 29 4 19 26 41 28 19 18 21 4 27 22 25 20 39 18 17 28 7 6 37 4
22
1 2 3 2 1 2 3 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1
30
25 27 30 34 39 45 52 60 69 79 69 60 52 45 39 34 30 26 22 18
82 78 74 70 66 67 64 60 65 80
0
output:
6
5
0
5
5
0
22
7
5
代码:
1 //poj1743
2 #include<cstdio>
3 #include<cstdlib>
4 #include<cstring>
5 #include<iostream>
6 using namespace std;
7
8 const int N=200010,INF=(int)1e9;
9 int n,a[N],c[N],sa[N],rk[N],Rs[N],y[N],wr[N],h[N];
10
11 int minn(int x,int y){return x<y ? x:y;}
12 int maxx(int x,int y){return x>y ? x:y;}
13
14 void get_sa(int cl,int m)
15 {
16 for(int i=1;i<=cl;i++) rk[i]=c[i];//c[i]必须>=1
17 for(int i=0;i<=m;i++) Rs[i]=0;
18 for(int i=1;i<=cl;i++) Rs[rk[i]]++;
19 for(int i=1;i<=m;i++) Rs[i]+=Rs[i-1];
20 for(int i=cl;i>=1;i--) sa[Rs[rk[i]]--]=i;
21
22 int ln=1,p=0;
23 while(p<cl)
24 {
25 int k=0;
26 for(int i=cl-ln+1;i<=cl;i++) y[++k]=i;
27 for(int i=1;i<=cl;i++)
28 if(sa[i]>ln) y[++k]=sa[i]-ln;
29 for(int i=1;i<=cl;i++)
30 wr[i]=rk[y[i]];
31
32 for(int i=0;i<=m;i++) Rs[i]=0;
33 for(int i=1;i<=cl;i++) Rs[wr[i]]++;
34 for(int i=1;i<=m;i++) Rs[i]+=Rs[i-1];
35 for(int i=cl;i>=1;i--) sa[Rs[wr[i]]--]=y[i];
36
37 for(int i=1;i<=cl;i++) wr[i]=rk[i];
38 for(int i=cl+1;i<=cl+ln;i++) wr[i]=0;//debug:rk[i]不能等于0的原因:这里给没有第二关键字的补0了。
39 p=1;rk[sa[1]]=1;
40 for(int i=2;i<=cl;i++)
41 {
42 if(wr[sa[i]]!=wr[sa[i-1]] || wr[sa[i]+ln]!=wr[sa[i-1]+ln]) p++;//debug '!='
43 rk[sa[i]]=p;
44 }
45 ln*=2;m=p;//debug
46 }
47 sa[0]=0;rk[0]=0;
48 }
49
50 void get_height(int cl)
51 {
52 int k=0;
53 for(int i=1;i<=cl;i++) if(rk[i]!=1)
54 {
55 int j=sa[rk[i]-1];
56 if(k) k--;
57 while(c[i+k]==c[j+k] && i+k<=cl && j+k<=cl) k++;
58 h[rk[i]]=k;
59 }
60 h[1]=0;
61 }
62
63 bool check(int cl,int k)
64 {
65 int fir=1,mn=INF,mx=0;
66 for(int i=1;i<=cl;i++)
67 {
68 if(h[i]<k)
69 {
70 if(mx-mn>k) return 1;//debug:>=改成>才能保证差值不重复的情况下音符也不重复(第一个音符没有算进去)
71 fir=i;mn=INF;mx=0;
72 }
73 else
74 {
75 mn=minn(mn,sa[i-1]);
76 mx=maxx(mx,sa[i-1]);
77
78 }
79 mn=minn(mn,sa[i]);
80 mx=maxx(mx,sa[i]);
81 }
82 if(mx-mn>k) return 1;//debug:最后一组不可忽略。
83 return 0;
84 }
85
86 int main()
87 {
88 freopen("a.in","r",stdin);
89 freopen("a.out","w",stdout);
90 while(1)
91 {
92 scanf("%d",&n);
93 if(!n) return 0;
94 int mx=-1,pre=0,mn=INF;
95 for(int i=1;i<=n;i++)
96 {
97 int x;
98 scanf("%d",&x);
99 c[i]=x-pre;
100 pre=x;
101 mx=maxx(mx,c[i]);
102 mn=minn(mn,c[i]);
103 }
104 for(int i=1;i<=n;i++) c[i]=c[i]-mn+1;//debug 因为rk[i]不能=0,c[i]也不能=0
105 mx=mx-mn+1;
106 get_sa(n,mx);
107 get_height(n);
108 int l=0,r=n;
109 while(l<r)
110 {
111 int mid=(l+r+1)/2;
112 if(check(n,mid-1)) l=mid;
113 else r=mid-1;
114 }
115 if(l>=5) printf("%d
",l);
116 else printf("0
");
117 }
118 return 0;
119 }