给出两个字符串 (S) 和 (T),长度分别为 (n) 和 (m),要求求出两个数组 (A) 和 (B):
(A) 存 (T) 的每一个后缀与 (T) 的最长公共前缀长度,(B) 存 (S) 的每一个后缀与 (T) 的最长公共前缀长度。
我们设我们有一个数组 ( ext{extend}),其中 ( ext{extend}[i]) 表示 (S[idots n]) 与 (T) 的最长公共前缀长度。
则 ( ext{extend}) 即为我们所求的 (B)。
那么,我们如何来求这个 ( ext{extend}) 呢?先来看一组样例:

我们求出 ( ext{extend}[1]) 之后,若暴力求 ( ext{extend}[2]),会差不多重新扫描一遍字符串。
当字符串的长度足够长时,时间开销会很大。所以我们要想办法避免重复扫描一些已经确定相等的字符串。
这里我们设另一个数组 ( ext{next}),其中 ( ext{next}[i]) 表示 (T[idots m]) 与 (T) 的最长公共前缀长度。也就是题目中所求 (A)。
在上面这张图中,我们可以看到,( ext{next}[2]=18),即 (T[1dots 18]=T[2dots 19])。
又因为 (S[1dots 19]=T[1dots 19]),所以 (S[2dots 19]=T[2dots 19]),所以 (T[1dots 18]=S[2dots 19])。
说明了什么?说明我们在求 ( ext{extend}[2]) 的时候,它的前 (18) 位都已经匹配成功了,直接从 (S[20]) 和 (T[19]) 开始匹配就可以了。
这也是 KMP 的思想,根据这个原理我们来研究扩展 KMP(Z 函数)。
扩展 KMP 求 ( ext{extend}) 有两种情况。
先看一张图:
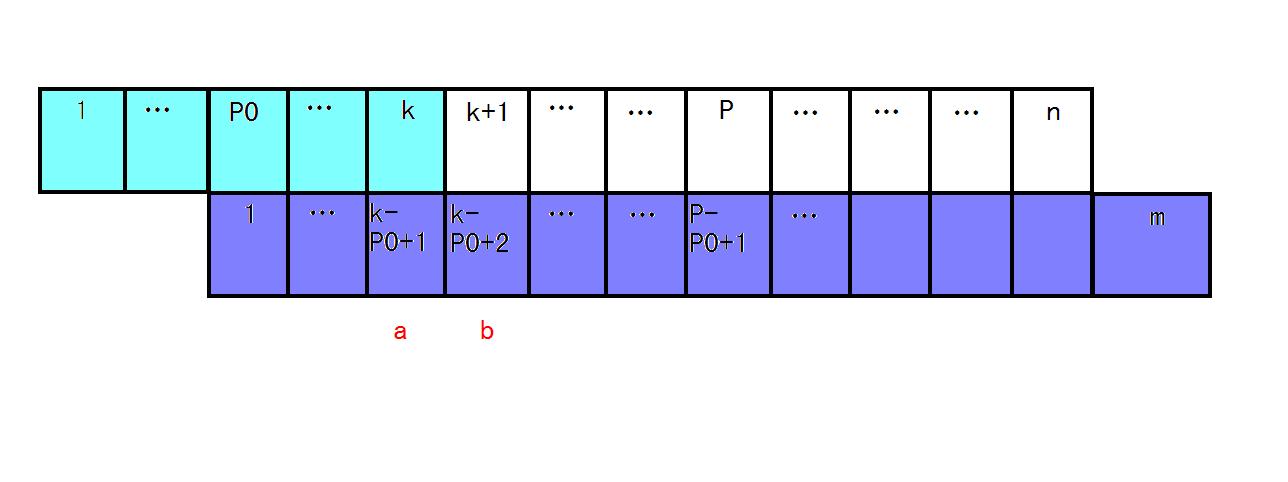
在这张图中,我们设上面的串为 (S),下面的串为 (T)。
此时,在 (iin [1,k]) 的 ( ext{extend}[i]) 已结完全求得。并且 (P=max{ ext{extend}[i]+i}),我们令这个得到最大值的 (i) 等于 (P0)。
然后我们令 (b=k-P0+2),并记 (L= ext{next}[b])。( ext{next}) 的定义同上。
接下来分析两种情况:
情况一 (k+L<P)

如图所示,此时绿线 (=) 蓝线 (=) 红线 (=L)。
因为 ( ext{extend}[P0] + P0 = P),根据 ( ext{extend}) 的定义,我们可知 (S[k+1dots P]=T[k-P0+2dots P-P0+1]),所以绿线 (=) 红线。
又因为 (L= ext{next}[b]),所以 (T[1dots L] = T[bdots b+L-1]),所以红线 (=) 蓝线。
也就是说,此时 ( ext{extend}[k+1]= ext{next}[b]=L)。而 (k+1) 刚好是我们现在要求的值。
这一部分的代码如下:
if(i+nxt[i-p0]<extend[p0]+p0) extend[i]=nxt[i-p0];
//i 就是 k+1,extend[p0]+p0 就是 p,nxt[i-p0] 就是 L。
//代码中下标是从 0 开始的,所以左侧不需要减去 1。
情况二 (k+Lge P)

如图所示,此时蓝线 (=) 红线 (=L)。
我们假设 (L-(P-k)=x),也就是这三条线末端被框起来的部分为 (x)。
倘若这三个长为 (x) 的部分不存在,那么绿线 (=) 蓝线 (=) 红线 (=P-k)。理由同情况一。
那么我们假设这三条线各延伸 (x) 长度后,绿线 (=) 蓝线 (=) 红线仍然成立。
但是剩下的这 (x) 我们无从得知,所以需要暴力匹配。因为前面大部分的已经可以直接得出相等了,所以后面的 (x) 不会很大,时间开销也不会很大。
这一部分的代码如下:
int now=extend[p0]+p0-i;now=max(now,0*1ll);//now 就是我们需要延伸的 L
while(t[now]==s[now+i]&&now<m&&now+i<n) now++;//延伸过程
extend[i]=now;p0=i;
所以 ( ext{extend}) 就可以求出来了。
但是我们好像忘了另一件事——( ext{next}) 还没求出来呢。
不过我们看一下它们的定义,( ext{extend}) 求的是 (S) 的后缀与 (T) 的关系,( ext{next}) 求的是 (T) 的后缀与 (T) 的关系。
看上去差不多。所以我们让 (T) 和自己跑一遍这个过程就可以求出来了。
但是注意我们要先单独求出第二位的 ( ext{next}) 再从第二位开始暴力,为的是防止求第一位时引用自己的值。
如此,扩展 KMP(Z 函数)的时间复杂度为 (Theta(n))。
总代码如下:
#include<queue>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define maxn 20001000
#define INF 0x3f3f3f3f
#define int long long
using namespace std;
int q,n,m,ans1,ans2;
char s[maxn],t[maxn];
int nxt[maxn],extend[maxn];
//nxt[i] 表示 T[i ~ m] 与 T[1 ~ m] 的最长公共前缀长度
//extend[i] 表示 S[i ~ n] 与 T[1 ~ m] 的最长公共前缀长度
int read(){
int s=0,w=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9')s=(s<<1)+(s<<3)+ch-'0',ch=getchar();
return s*w;
}
void Getnxt(){
nxt[0]=m;//T 与 T 的最长公共前缀是它自己
int now=0,p0=1;
while(t[now]==t[1+now]&&now+1<m) now++;
nxt[1]=now;
for(int i=1;i<m;i++){
if(i+nxt[i-p0]<nxt[p0]+p0) nxt[i]=nxt[i-p0];
else{
int now=p0+nxt[p0]-i;now=max(now,0*1ll);
while(now+i<m&&t[now]==t[now+i]) now++;
nxt[i]=now;p0=i;
}
}
}
void Exkmp(){
Getnxt();//处理 nxt[]
int now=0,p0=0;
while(s[now]==t[now]&&now<m&&now<n) now++;
extend[0]=now;
for(int i=1;i<n;i++){
if(i+nxt[i-p0]<extend[p0]+p0) extend[i]=nxt[i-p0];
//nxt[i-p0] 是 L
//extend[p0]+p0 是 p
//i 是 k + 1
//下标从 0 开始不用减 1.
else{
int now=extend[p0]+p0-i;now=max(now,0*1ll);
while(t[now]==s[now+i]&&now<m&&now+i<n) now++;
extend[i]=now;p0=i;
}
}
}
signed main(){
scanf("%s%s",s,t);
n=strlen(s);m=strlen(t);Exkmp();
for(int i=0;i<m;i++)ans1^=(i+1)*(nxt[i]+1);
for(int i=0;i<n;i++)ans2^=(i+1)*(extend[i]+1);
printf("%lld
%lld
",ans1,ans2);
return 0;
}