求出所有排列 去重全排列 回溯算法

一、"alibaba"这个字符串有多少种排序方法

二、去重全排列

方法1：去重的全排列就是从第一个数字起，每个数分别与它后面非重复出现的数字交换（重复数据第一个交换之后不交换）。

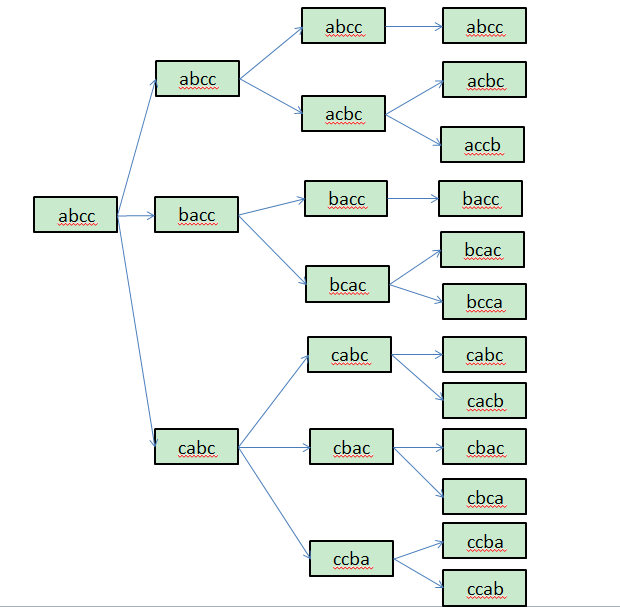
（1）第一个字符a与后面的字符交换得到abcc(不交换)、bacc（和b交换）、cabc（和c交换）,因为第四位的c和第三位相同，所以a和第四位不交换。

（2）以此类推，直到最后一个字符。

（3）代码

import java.util.ArrayList;
import java.util.Collections;
import java.util.Set;
import java.util.HashSet;
public class Solution {
    public ArrayList<String> Permutation(String str) {
        ArrayList<String> list = new ArrayList<String>();
        if(str != null && str.length()>0){
            PermutationHelper(str.toCharArray(), 0, list);//整个字符串排序
           // Collections.sort(list);
            Collections.sort(list);//对list中数据进行字典排序
        }
        return list;
    }
    
    public void PermutationHelper(char[] chars, int i, ArrayList<String> list){
        if(i == chars.length-1){
            list.add(String.valueOf(chars));
        }else{
            Set<Character> charSet = new HashSet<Character>();
            for(int j = i; j<chars.length; j++){
                if(j==i || !charSet.contains(chars[j])){
                    charSet.add(chars[j]);
                    swap(chars,i,j);//交换得到chars
                    PermutationHelper(chars,i+1,list);//固定前i个元素之后的字符串排序结果chars
                    swap(chars,j,i);//交换回来
                }
                
            }
        }
    }
    public void swap(char[] chars,int i,int j){
        char temp = chars[i];
        chars[i] = chars[j];
        chars[j] = temp;
    }
        
}

方法2：回溯法

1.回溯法定义：

回溯法（探索与回溯法）是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

2.参考

https://blog.csdn.net/versencoder/article/details/52071930

https://blog.csdn.net/versencoder/article/details/52072350

 3.解题思路

问题：给两个整数 n和k，从1---n中选择k数字的组合。比如n=4，k=2，那么从1,2,3,4中选取两个数字的组合，包括如下所述的四种。

[

 [2,4],

 [3,4],

 [2,3],

 [1,2],

 [1,3],

 [1,4],

]

题目所给框架：

public class Solution {

   public List<List<Integer>> combine(int n, int k) {

       

    }

}

（1）要求返回的类型是List<List<Integer>> 也就是说将所有可能的组合list（由整数构成）放入另一个list（由list构成）中。要求返回List<List<Integer>>，那么 定义一个全局变量

List<List<Integer>> result=new ArrayList<List<Integer>>();

（2）定义一个辅助的方法（函数），其中n,k是题目要求的变量，List<Integer>list是数字的组合，也是需要的。

public void backtracking(int n,int k, List<Integer>list){}

（3）如何实现这个算法？对于n=4，k=2，1,2,3,4中选2个数字，我们可以做如下尝试，加入先选择1，注意这时候k=1了（此时只需要选择1个数字），那我们只需要从（2----4）中再选择一个数字（调用backtracking（））。每次选择一个加入我们的链表list中，此时找到[1,2]，[1,3]，[1,4]。之后选择2作为第一个数字，在从（3---4）中查找剩余的一个，以此类推。那什么时候结束呢？当然是k<0的时候，这时候都选完了。

publicvoid backtracking(int n,int k,int start,List<Integer> list){
        if(k<0)        return;
        else if(k==0){
                       //k==0表示已经找到了k个数字的组合，这时候加入全局result中
            result.add(new ArrayList(list));
 
        }else{
            for(int i=start;i<=n;i++){//start表示开始的位置，开始点加入list中，再从开始点之后查找剩余数字
                list.add(i);//尝试性的加入i
                    //开始回溯啦，下一次要找的数字减少一个所以用k-1，i+1见后面分析
                backtracking(n,k-1,i+1,list);
                //（留白，有用=。=）
            }
        }
    }

（4）在循环中调用backtracking(n,k-1,i+1,list);时，list在之后已经又加入了一个数字，所以要回退一个数字，之后在查找。例如backtracking(4,2,1,null)，在for循环中，list.add(1)，之后调用backtracking(4,1,2,[1])，在调用backtracking(4,1,2,[1])中开启第一次循环返回[1,2]，第二次循环若没有回退，则会在原有[1,2]基础上list.add(3),。所以回退应该在留白处回退到初始地方，再向下继续查找。所以完整的程序如下：

public class Solution {
   List<List<Integer>> result=new ArrayList<List<Integer>>();
   public List<List<Integer>> combine(int n, int k) {
       List<Integer> list=new ArrayList<Integer>();
       backtracking(n,k,1,list);
       return result;
    }
   public void backtracking(int n,int k,int start,List<Integer>list){
       if(k<0) return ;
       else if(k==0){
           result.add(new ArrayList(list));
       }else{
           for(int i=start;i<=n;i++){
                list.add(i);
                backtracking(n,k-1,i+1,list);
                list.remove(list.size()-1);
            }
       }
    }
}